拓扑排序的应用

Posted 2023-03-23

如题
拓扑排序在哪些方面有应用,及其发展趋势?
谢谢

参考技术A 一个复杂的工程通常可以分解成一组小任务的集合，完成这些小任务意味着整个工程的完成。例如，汽车装配工程可分解为以下任务：将底盘放上装配线，装轴，将座位装在底盘上，上漆，装刹车，装门等等。任务之间具有先后关系，例如在装轴之前必须先将底板放上装配线。任务的先后顺序可用有向图表示——称为顶点活动（ Activity On Vertex, AOV）网络。有向图的顶点代表任务，有向边(i, j) 表示先后关系：任务j 开始前任务i 必须完成。图1 - 4显示了六个任务的工程，边（ 1 , 4）表示任务1在任务4开始前完成，同样边（ 4 , 6）表示任务4在任务6开始前完成，边（1 , 4）与（4 , 6）合起来可知任务1在任务6开始前完成，即前后关系是传递的。由此可知，边（1 , 4）是多余的，因为边（1 , 3）和（3 , 4）已暗示了这种关系。

在很多条件下，任务的执行是连续进行的，例如汽车装配问题或平时购买的标有“需要装配”的消费品（自行车、小孩的秋千装置，割草机等等）。我们可根据所建议的顺序来装配。在由任务建立的有向图中，边（ i, j）表示在装配序列中任务i 在任务j 的前面，具有这种性质的序列称为拓扑序列（topological orders或topological sequences)。根据任务的有向图建立拓扑序列的过程称为拓扑排序（topological sorting）。图1 - 4的任务有向图有多种拓扑序列，其中的三种为1 2 3 4 5 6，1 3 2 4 5 6和2 1 5 3 4 6，序列1 4 2 3 5 6就不是拓扑序列，因为在这个序列中任务4在3的前面，而任务有向图中的边为（ 3 , 4），这种序列与边（ 3 , 4）及其他边所指示的序列相矛盾。可用贪婪算法来建立拓扑序列。算法按从左到右的步骤构造拓扑序列，每一步在排好的序列中加入一个顶点。利用如下贪婪准则来选择顶点：从剩下的顶点中，选择顶点w，使得w 不存在这样的入边（ v,w），其中顶点v 不在已排好的序列结构中出现。注意到如果加入的顶点w违背了这个准则（即有向图中存在边（ v,w）且v 不在已构造的序列中），则无法完成拓扑排序，因为顶点v 必须跟随在顶点w 之后。贪婪算法的伪代码如图1 3 - 5所示。while 循环的每次迭代代表贪婪算法的一个步骤。

现在用贪婪算法来求解图1 - 4的有向图。首先从一个空序列V开始，第一步选择V的第一个顶点。此时，在有向图中有两个候选顶点1和2，若选择顶点2，则序列V = 2，第一步完成。第二步选择V的第二个顶点，根据贪婪准则可知候选顶点为1和5，若选择5，则V = 2 5。下一步，顶点1是唯一的候选，因此V = 2 5 1。第四步，顶点3是唯一的候选，因此把顶点3加入V

得到V = 2 5 1 3。在最后两步分别加入顶点4和6 ，得V = 2 5 1 3 4 6。

1. 贪婪算法的正确性

为保证贪婪算法算的正确性，需要证明： 1) 当算法失败时，有向图没有拓扑序列； 2) 若

算法没有失败，V即是拓扑序列。2) 即是用贪婪准则来选取下一个顶点的直接结果， 1) 的证明见定理1 3 - 2，它证明了若算法失败，则有向图中有环路。若有向图中包含环qj qj + 1.qk qj , 则它没有拓扑序列，因为该序列暗示了qj 一定要在qj 开始前完成。

定理1-2 如果图1 3 - 5算法失败，则有向图含有环路。

证明注意到当失败时| V |<n, 且没有候选顶点能加入V中，因此至少有一个顶点q1 不在V中，有向图中必包含边（ q2 , q1）且q2 不在V中，否则， q1 是可加入V的候选顶点。同样，必有边（q3 , q2）使得q3 不在V中，若q3 = q1 则q1 q2 q3 是有向图中的一个环路；若q3 ≠q1，则必存在q4 使（q4 , q3）是有向图的边且q4 不在V中，否则，q3 便是V的一个候选顶点。若q4 为q1 , q2 , q3 中的任何一个，则又可知有向图含有环，因为有向图具有有限个顶点数n，继续利用上述方法，最后总能找到一个环路。

2. 数据结构的选择

为将图1 - 5用C + +代码来实现，必须考虑序列V的描述方法，以及如何找出可加入V的候选顶点。一种高效的实现方法是将序列V用一维数组v 来描述的，用一个栈来保存可加入V的候选顶点。另有一个一维数组I n D e g r e e，I n D e g r e e[ j ]表示与顶点j相连的节点i 的数目，其中顶点i不是V中的成员，它们之间的有向图的边表示为（ i, j）。当I n D e g r e e[ j ]变为0时表示j 成为一个候选节点。序列V初始时为空。I n D e g r e e[ j ]为顶点j 的入度。每次向V中加入一个顶点时，所有与新加入顶点邻接的顶点j，其I n D e g r e e[ j ]减1。对于有向图1 - 4，开始时I n D e g r e e [ 1 : 6 ] = [ 0 , 0 , 1 , 3 , 1 , 3 ]。由于顶点1和2的I n D e g r e e值为0，因此它们是可加入V的候选顶点，由此，顶点1和2首先入栈。每一步，从栈中取出一个顶点将其加入V，同时减去与其邻接的顶点的I n D e g r e e值。若在第一步时从栈中取出顶点2并将其加入V，便得到了v [ 0 ] = 2，和I n D e g r e e [ 1 : 6 ] = [ 0 , 0 , 1 , 2 , 0 , 3 ]。由于I n D e g r e e [ 5 ]刚刚变为0，因此将顶点5入栈。

程序1 3 - 2给出了相应的C + +代码，这个代码被定义为N e t w o r k的一个成员函数。而且，它对于有无加权的有向图均适用。但若用于无向图（不论其有无加权）将会得到错误的结果，因为拓扑排序是针对有向图来定义的。为解决这个问题，利用同样的模板来定义成员函数AdjacencyGraph, AdjacencyWGraph，L i n k e d G r a p h和L i n k e d W G r a p h。这些函数可重载N e t w o r k中的函数并可输出错误信息。如果找到拓扑序列，则Topological 函数返回t r u e；若输入的有向图无拓扑序列则返回f a l s e。当找到拓扑序列时，将其返回到v [ 0 :n- 1 ]中。

3. Network:Topological 的复杂性

第一和第三个f o r循环的时间开销为(n )。若使用（耗费）邻接矩阵,则第二个for 循环所用的时间为(n2 )；若使用邻接链表,则所用时间为(n+e)。在两个嵌套的while 循环中，外层循环需执行n次，每次将顶点w 加入到v 中，并初始化内层while 循环。使用邻接矩阵时，内层w h i l e循环对于每个顶点w 需花费(n)的时间；若利用邻接链表，则这个循环需花费dwout 的时间，因此，内层while 循环的时间开销为(n2 )或(n+e)。所以，若利用邻接矩阵，程序1 3 - 2的时间复杂性为(n2 )，若利用邻接链表则为(n+e)。

程序13-2 拓扑排序

bool Network::Topological(int v[])

// 计算有向图中顶点的拓扑次序

// 如果找到了一个拓扑次序，则返回t r u e，此时，在v [ 0 : n - 1 ]中记录拓扑次序

// 如果不存在拓扑次序，则返回f a l s e

int n = Ve r t i c e s ( ) ;

// 计算入度

int *InDegree = new int [n+1];

InitializePos(); // 图遍历器数组

for (int i = 1; i <= n; i++) // 初始化

InDegree[i] = 0;

for (i = 1; i <= n; i++) // 从i 出发的边

int u = Begin(i);

while (u)

I n D e g r e e [ u ] + + ;

u = NextVe r t e x ( i ) ;



// 把入度为0的顶点压入堆栈

LinkedStack<int> S;

for (i = 1; i <= n; i++)

if (!InDegree[i]) S.Add(i);

// 产生拓扑次序

i = 0; // 数组v 的游标

while (!S.IsEmpty()) // 从堆栈中选择

int w; // 下一个顶点

S . D e l e t e ( w ) ;

v[i++] = w;

int u = Begin(w);

while (u) // 修改入度

I n D e g r e e [ u ] - - ;

if (!InDegree[u]) S.Add(u);

u = NextVe r t e x ( w ) ;



D e a c t i v a t e P o s ( ) ;

delete [] InDegree;

return (i == n);

数据结构学习笔记——图的应用2（拓扑排序关键路径）

目录

• 一、拓扑排序
• • （一）DAG图和AOV网
  • （二）拓扑排序的概念
  • （三）拓扑排序的步骤
  • （四）拓扑排序的时间复杂度
• 二、逆拓扑排序和DFS算法的应用
• • （一）逆拓扑排序
  • （二）DFS算法的应用
• 三、关键路径
• • （一）AOE网
  • （二）源点和汇点
  • （三）关键路径的概念
  • （四）关键路径的算法步骤

一、拓扑排序

（一）DAG图和AOV网

• 对于一个有向图，若图中不存在回路（环），则称该图是一个DAG图；若以DAG图中的顶点表示活动，以边表示活动的先后次序，则称其是一个AOV网。

例如，这就是一个DAG图：

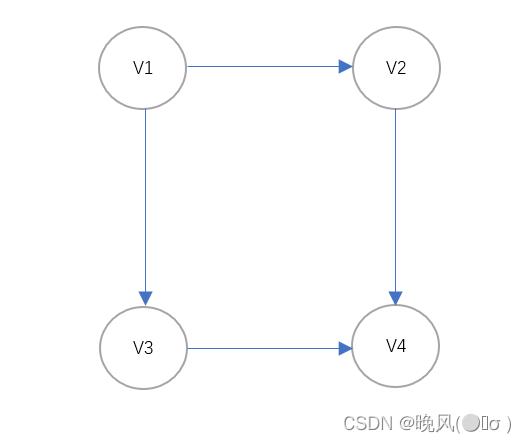
（二）拓扑排序的概念

• 对于一个DAG图，其所有顶点组成一个线性序列，且每个顶点只出现一次，对于图G=（V，E）中的任意一对顶点A和B，顶点A在线性序列中排在顶点B的前面，即<A，B>∈E(G)，图中存在由A到B的路径，则这种序列称为拓扑序列，称为拓扑排序。

若一个有向无回路图的拓扑序列是唯一的，对其而言并不能唯一确定该图。

（三）拓扑排序的步骤

对于一个AOV网进行拓扑排序：
1、从网中找选择一个没有前驱，即入度ID(v)=0的顶点；
2、删除该顶点且删除由该顶点的所有起始边（出度的边），并将该顶点输出；
3、重复(1)和(2)步骤，直至AOV网为空或不存在没有前驱的结点为止；
4、最后得到一个序列，即拓扑排序。

• AOV网的拓扑排序的序列不止一个，也可以能有多个，是由于当网中有多个入度为0的顶点时，进行拓扑排序，得到的序列不止一种。

例如，对于下面这个图，对其进行拓扑排序：

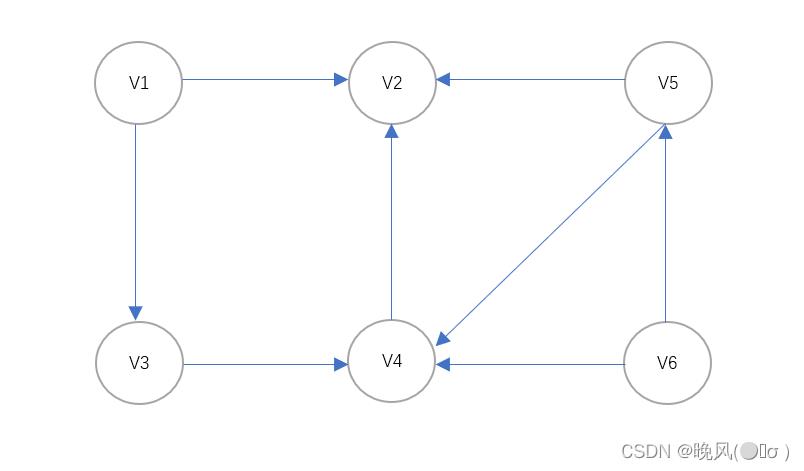
1、由该图可知，ID(V1)=0、ID(V6)=0，即入度为0的顶点有V1、V6。
2、以V1开始（若以V6序列开始也可以，只是得到的拓扑序列不同），删除顶点V1以及其出度并输出该顶点，得到如下：

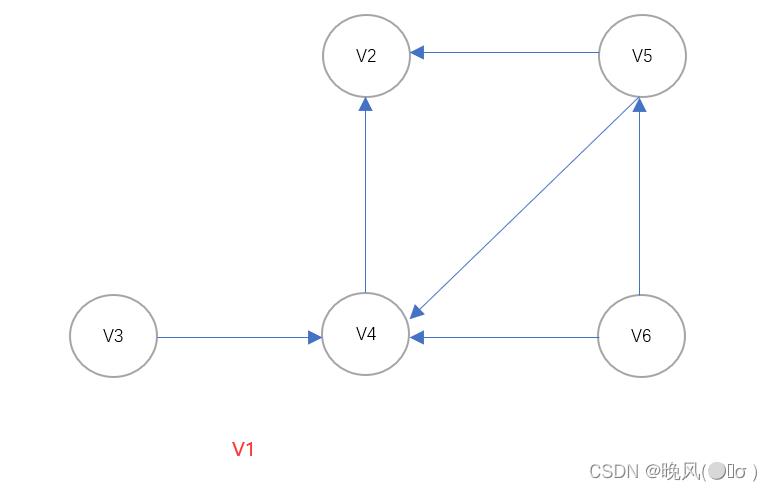
3、由得到的图可知，ID(V3)=0、ID(V6)=0，即入度为0的顶点为V3和V6，以V3继续（若以V6序列也可以，只是得到的拓扑序列不同），删除顶点V3以及其出度并输出该顶点，得到如下：

4、由得到的图可知，ID(V6)=0，即入度为0的顶点为V6，删除顶点V6以及其出度并输出该顶点，得到如下：

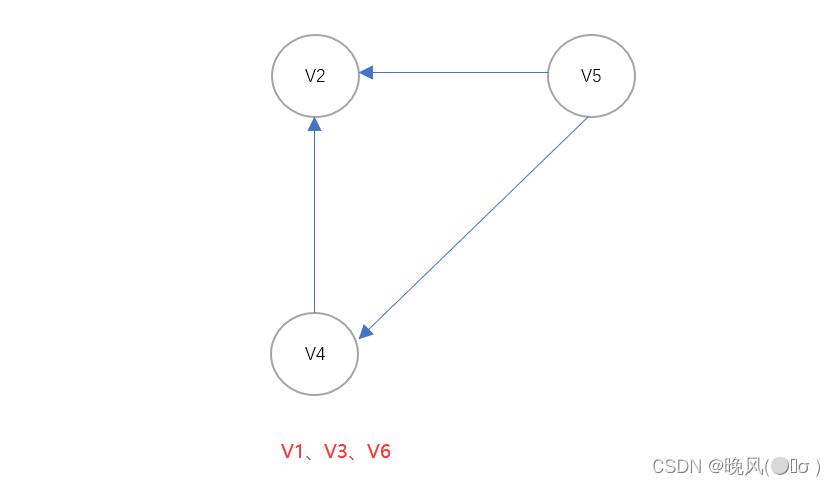
5、由得到的图可知，ID(V5)=0，即入度为0的顶点为V5，删除顶点V5以及其出度并输出该顶点，得到如下：

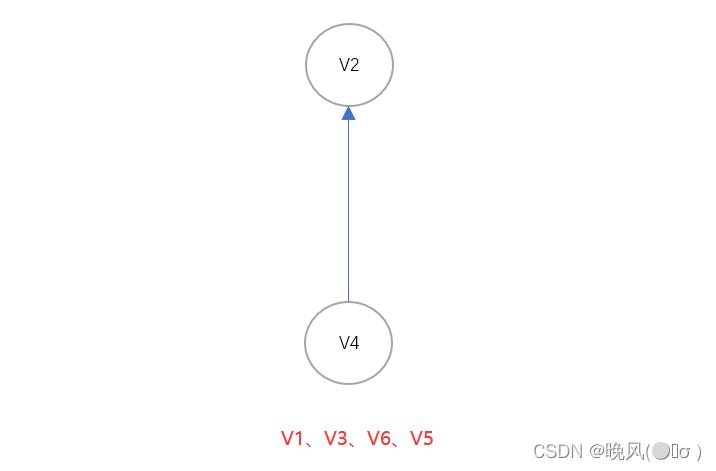
6、由得到的图可知，ID(V4)=0，即入度为0的顶点为V4，删除顶点V4以及其出度并输出该顶点，得到如下：

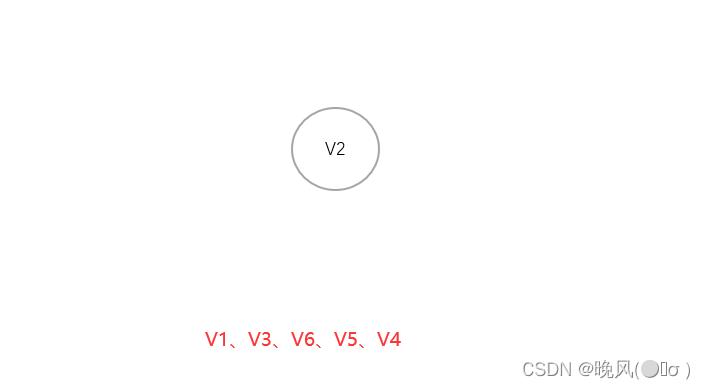
7、加上最后的顶点V2，输出该顶点，此时图中所有顶点都输出，即得到该图的一个拓扑序列为V1、V3、V6、V5、V4、V2。

（四）拓扑排序的时间复杂度

• 若一个有向图的所有顶点不能排成一个拓扑序列（有向图存在回路，则一定不存在拓扑排序），由于该图中一定存在回路，即该图中存在含有顶点数目大于1的强连通分量。
• 对于图G=（V，E），当采用邻接矩阵存储图时拓扑排序的时间复杂度为O(|V|²)；而采用邻接表存储图时，由于在输出顶点时还要删除其所有起始边（出度），所以拓扑排序的时间复杂度为O(|V|+|E|)。

二、逆拓扑排序和DFS算法的应用

（一）逆拓扑排序

若将拓扑排序的步骤中的一开始的针对入度进行排序改为针对出度，则以下是逆拓扑排序的步骤，对于一个AOV网进行逆拓扑排序：
1、从网中找选择一个没有后继，即出度OD(v)=0的顶点；
2、删除该顶点且删除由该顶点的所有终止边（入度的边），并将该顶点输出；
3、重复(1)和(2)步骤，直至AOV网为空或不存在没有后继的结点为止；
4、最后得到一个序列，即逆拓扑排序。

• 与拓扑排序一样，AOV网的逆拓扑排序的序列不止一个，也可以能有多个，是由于当网中有多个出度为0的顶点时，进行逆拓扑排序，得到的序列不止一种。

例如，对于下面这个图，对其进行拓扑排序：

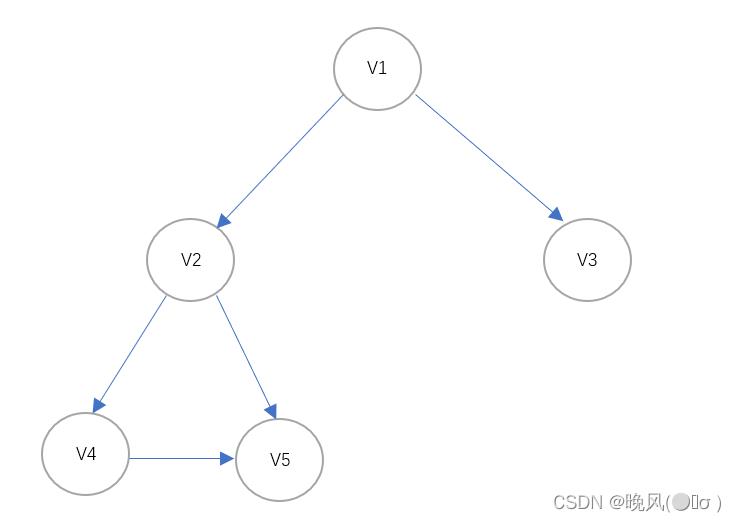
1、由该图可知，OD(V3)=0、OD(V5)=0，即出度为0的顶点有V3、V5。
2、以V3开始（若以V5序列开始也可以，只是得到的逆拓扑序列不同），删除顶点V3以及其入度并输出该顶点，得到如下：

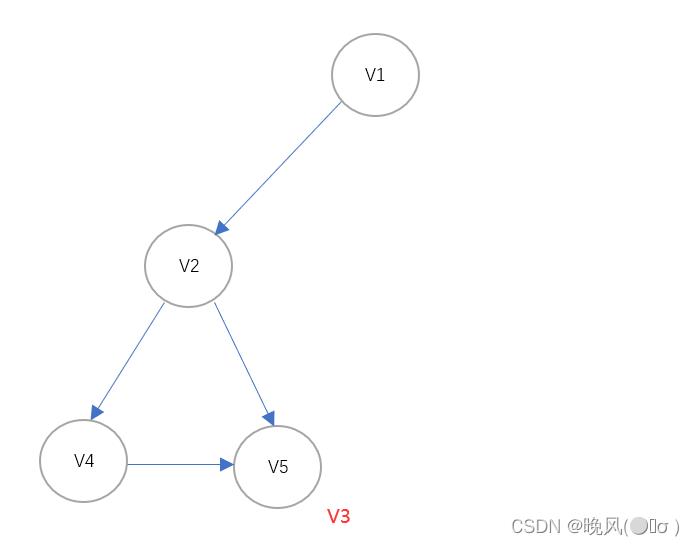
3、由得到的图可知，OD(V5)=0，即出度为0的顶点为V5，以V5继续，删除顶点V5以及其入度并输出该顶点，得到如下：

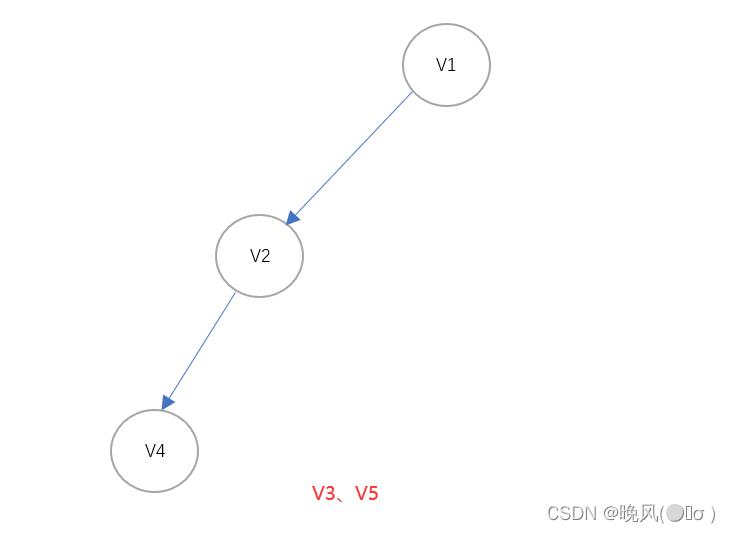
4、由得到的图可知，OD(V4)=0，即出度为0的顶点为V4，以V4继续，删除顶点V4以及其入度并输出该顶点，得到如下：

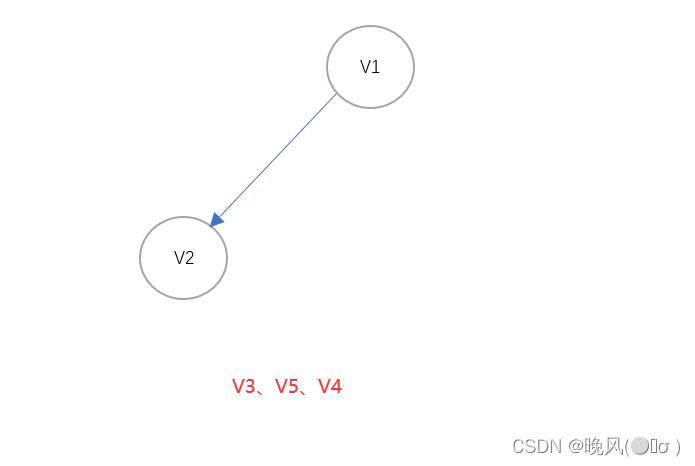
5、由得到的图可知，OD(V2)=0，即出度为0的顶点为V2，以V2继续，删除顶点V2以及其入度并输出该顶点，得到如下：

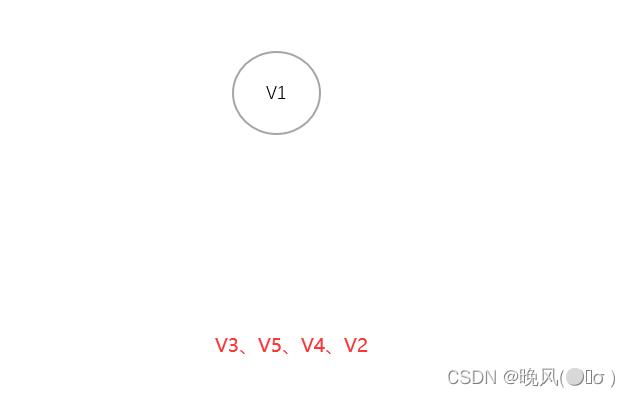
6、加上最后的顶点V1，输出该顶点，此时图中所有顶点都输出，即得到该图的一个逆拓扑序列为V3、V5、V4、V2、V1。

（二）DFS算法的应用

对于一个AOV网也可以采用DFS算法，由于当从有向无环图中某一顶点开始深度优先搜索时，最先得到的顶点即为出度等于0的顶点，所以通过DFS算法得到的顶点序列刚好为逆向的拓扑序列。（DFS算法的知识点可以看之前的文章：图的遍历算法（深度优先搜索和广度优先搜索））

三、关键路径

（一）AOE网

对于AOV网，它是以顶点来表示活动、边上无权值，只表示活动的先后次序；而对于AOE网，是以边来表示活动，且边上有权值，表示完成该活动的开销（时间），其对比如下表：

（二）源点和汇点

• 在一个表示工程的AOE网中，只存在一个入度等于0，即ID(v)=0的顶点，称为源点，代表整个工程的开始；同样，也只存在一个出度等于0，即OD(v)=0的顶点，称为汇点，代表整个工程的结束。

（三）关键路径的概念

• 在AOE网中，由源点到汇点的有向路径可能有多条，从而完成活动的路径长度也不同，将所有路径中具有最大路径长度的路径称为关键路径，且这条路径上的所有活动称为关键活动，是决定整个工程的关键因素，关键路径是整个工程所完成的最短时间。

一个AOE网的关键路径不唯一，若延长关键路径上的关键活动的时间，则整个工程的时间也会随着延长；另外，只有缩短所有的关键路径上共有的任意一个关键活动的持续时间，才会缩短关键路径长度。

（四）关键路径的算法步骤

1、根据所给的图，求得该图的拓扑有序序列和逆拓扑有序序列；
2、通过得到的序列，求得每个事件的最早发生时间和最迟发生时间：
3、根据(2)得到的结果，求得每个活动的最早发生时间和最迟发生时间。
4、根据(3)得到的结果，找到最早发生时间和最迟发生时间相同的活动，就得到了关键活动，由关键活动连成的路径即为关键路径。

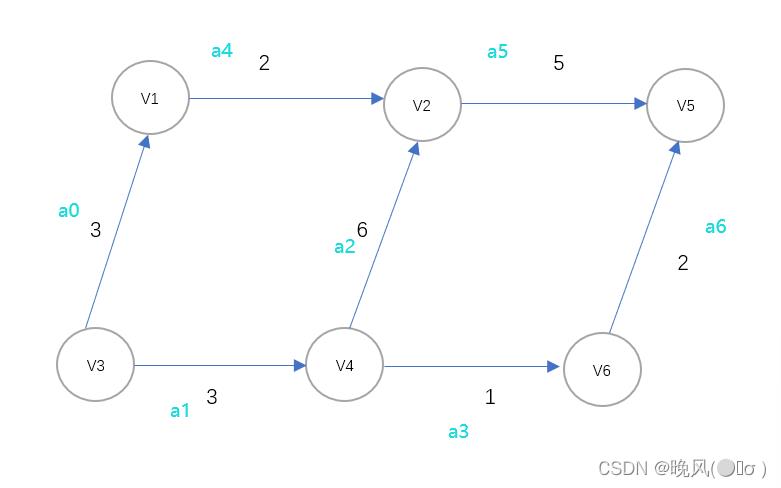
例如，下面是一个AOE网，求其关键路径。

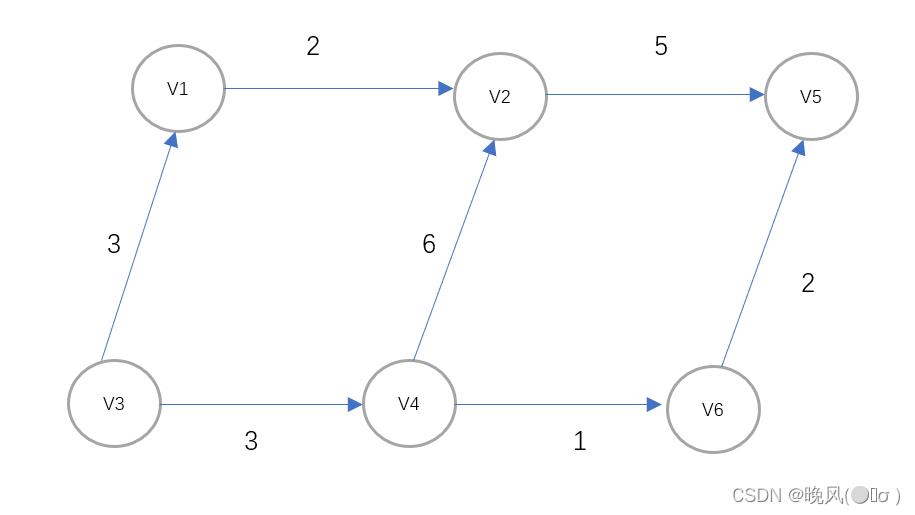
1、首先求其拓扑序列和逆拓扑序列：
拓扑序列和逆拓扑序列分别为V3、V1、V4、V2、V6、V5和V5、V6、V2、V4、V1、V3。
2、设ve(V)为顶点V代表的事件的最早发生时间，依照拓扑序列的先后顺序求各顶点所对应事件的最早发生时间：
设事件0的开始时间为0，即ve(V3)=0，可得：
ve(V1)=ve(V3)+3=0+3=3；
ve(V4)=ve(V3)+3=0+3=3；
由于到V2的路径有两条，分别是V1→V2和V4→V2，要取其中权值最大者，也就是最早发生时间，ve(V2)=maxve(V1)+2，ve(V4)+6=max3+2，3+6=9；
ve(V6)=ve(V4)+1=3+1=4；
由于到V5的路径有两条，分别是V2→V5和V6→V5，要取其中权值最大者，也就是最早发生时间，ve(V5)=maxve(V2)+5，ve(V6)+2=max9+5，4+2=14。
3、设vl(V)为顶点V代表的事件的最迟发生时间，最迟发生时间是在不推迟整个工程完成的前提下，该事件最迟必须发生的时间，依照逆拓扑序列的先后顺序求各顶点所对应事件的最迟发生时间，且由事件的最早发生时间，可得：
vl(V5)=ve(V5)=14；
vl(V6)=vl(V5)-2=14-2=12；
vl(V2)=vl(V5)-5=14-5=9；
由于回V4的路径有两条，分别是V3→V1和V3→V4，要取其中权值最小者，也就是最迟发生时间，vl(V4)=minvl(V2)-6，vl(V6)-1=min9-6，12-1=3；
vl(V1)=vl(V2)-2=9-2=7；
由于回V3的路径有两条，分别是V4→V2和V4→V6，要取其中权值最小者，也就是最迟发生时间，vl(V3)=minvl(V1)-3，vl(V4)-3=min7-3，3-3=0。
4、求每个活动的最早发生时间和最迟发生时间，设e(ak)和l(ak)为当前活动ak的最早发生时间和最迟发生时间，由于事件代表一个新活动的开始或旧活动的结束，所以事件的最早发生时间就是由这个事件所发出的活动的最早发生时间，即ve(V)；而活动的最迟发生时间是事件的最迟发生时间减去以它为结束点的活动的持续时间：

（1）活动的最早发生时间：
e(a0)=e(a1)=ve(V3)=0；
e(a2)=e(a3)=ve(V4)=3；
e(a4)=ve(V1)=3；
e(a5)=ve(V2)=9；
e(a6)=ve(V6)=4。
（2）活动的最迟发生时间：
l(a0)=vl(V1)-3=7-3=4；
l(a1)=vl(v4)-3=3-3=0；
l(a2)=vl(V2)-6=9-6=3；
l(a3)=vl(V6)-1=12-1=11；
l(a4)=vl(V2)-2=9-2=7；
l(a5)=vl(V5)-5=14-5=9；
l(a6)=vl(V5)-2=14-2=12；
由以上得到的活动的最早/最迟发生时间，整理得关键活动，即最早最早发生时间和最迟发生时间相同的活动，如下：

活动	最早发生时间	最迟发生时间	关键活动
a0	0	4
a1	0	0	√
a2	3	3	√
a3	3	11
a4	3	7
a5	9	9	√
a6	4	12

5、由关键活动所连成的路径即为所求的关键路径，可知关键路径为：
V3→V4→V2→V5，
关键路径所持续的时间为整个工程所持续的时间（整个图中所有活动完成的时间）：
a1+a2+a5=0+3+9=12。

例、下图所示的AOE网表示一项包含8个活动的工程，求活动d的最早开始时间和最迟开始时间。

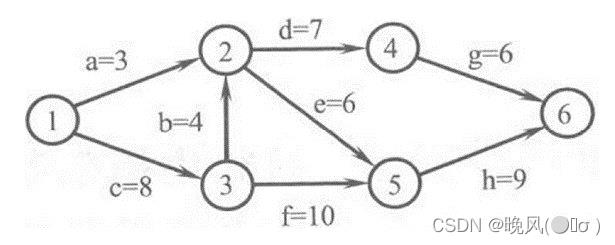
解：活动d的最早开始时间为事件2的最早发生时间，即maxa，b+c=max3，12=12；求出图的关键路径长度，先求得拓扑排序为1、3、2、4、5、6：
设ve(1)=0，
ve(2)=ve(1)+3=3；
ve(3)=ve(1)+8=8；
ve(4)=ve(2)+7=10；
ve(5)=maxve(2)+6，ve(3)+10=max9，18=18；
ve(6)=maxve(4)+6，ve(5)+9=max16，27=27；
所以关键路径长度为27。
由于活动d的最迟开始时间为该活动弧的终点所表示的事件的最迟发生时间与该活动所需时间之差，即min27-g=min21，
所以活动的最迟开始时间为21-d=21-7=14。