2023美国大学生数学建模竞赛（美赛）思路&代码

Posted 凌青羽

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2023美国大学生数学建模竞赛（美赛）思路&代码相关的知识，希望对你有一定的参考价值。

2023美国大学生数学建模竞赛（美赛）思路&代码

报名

官方网址:http://www.comapmath.com/MCMICM/index.html

时间节点

1.官方报名截止时间：2023 年2 月17 日上午0点
2.比赛开始时间：2023 年2 月17 日上午6点
3.比赛结束时间：2023 年2 月21 日上午9点

比赛说明

问题A（数据分析题）：收干旱影响的植物群落（MCM）

  • 赛题目的：分析干旱程度与植物群落中物种数量的关系
  • 赛题解读&解题思路链接：
    （1）这道题的难点是寻找数据，如果能找到干旱程度的适应性代表的指标以及对应植物群落物种的数量，那这道题基本上是迎刃而解，只需要简单去搭建一个预测模型即可仿真
    （2）目标是对马萨马拉这个大型野生动物保护区进行推荐不同区域的管理策略

第一问

1.问题定义

  • 目标函数Y：植物群落的总占地面积+群落内各类植物的数量（需要归一化量纲，不同植物体积不同，总数量不同）
  • 影响因素：天气因素（是否干旱，此处量化为降水量R与太阳光功率S）、物种的种类数量 物种之间的相互作用（比如相关性，共生性）
    • 物种之间的相互作用：为同类植物，则相关性较强，不同类植物相关性较弱，相关性的量化可以参照植物种类大纲，定义相关性指标系数 ，相互作用因子 ，通过拟合得到
    • 定义此指标的目的就在于为了使模型更具有普遍性和适用性不同地区物种不同，A地可能大多是仙人掌之类但是B地是树木灌丛类。同一模型可以针对多种自然环境，增加模型的适用性。物种之间的正面影响因素，物种之间的负面影响因素。
    • 太阳光功率可以用（一天之内温度的总和*Aera）

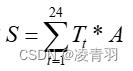
      一般来讲R与S成负相关 （自己加个小模型验证就可以）
  • 太阳光功率在一天内的变化：

优化模型：计算一天的太阳光功率需要考虑太阳辐射的强度和时间的变化。太阳辐射的强度与太阳高度角、大气透过率、地球表面倾角等因素有关，因此需要进行一定的模拟和计算。

以下是一个示例代码，展示如何使用Python计算一天的太阳光功率：

import numpy as np

# 太阳直射辐射强度，单位：瓦/平方米
solar_constant = 1367

# 太阳高度角和方位角的范围，单位：弧度
altitude_range = np.arange(-np.pi/2, np.pi/2+0.01, 0.01)
azimuth_range = np.arange(-np.pi, np.pi+0.01, 0.01)

# 地球自转周期，单位：小时
day_length = 24

# 日内时刻，从早上6点到晚上6点，每隔10分钟记录一次
time_range = np.arange(6, 18.1, 0.01)

# 计算每个时刻的太阳光功率
solar_power = []
for t in time_range:
    # 计算太阳高度角和方位角
    hour_angle = (t-12)/12 * np.pi
    declination = 23.45 * np.sin(2*np.pi*(284+t)/365)
    altitude = np.arcsin(np.sin(declination)*np.sin(23.45*np.pi/180) + np.cos(declination)*np.cos(hour_angle)*np.cos(23.45*np.pi/180))
    azimuth = np.arccos((np.sin(declination)*np.cos(altitude)-np.sin(altitude)*np.cos(23.45*np.pi/180))/(np.cos(altitude)*np.sin(23.45*np.pi/180)))
    if hour_angle > 0:
        azimuth = -azimuth

    # 计算太阳直射辐射强度
    cos_theta = np.sin(altitude)*np.sin(30*np.pi/180) + np.cos(altitude)*np.cos(30*np.pi/180)*np.cos(azimuth-(-np.pi/2))
    tau = 0.7**((altitude*180/np.pi)/10)
    s = solar_constant * cos_theta * tau
    if np.isnan(s):
        continue
    solar_power.append(s)

# 将每个时刻的太阳光功率相加，得到一天的太阳光功率
daily_solar_power = np.sum(solar_power) * day_length * 60 * 60

print('一天的太阳光功率为：%.2f千瓦时' % (daily_solar_power/1000))

结果：

一天的太阳光功率为：18506091.09千瓦时

2.建立预测函数
根据查询的文献：建立预测函数（此函数自己定义，也可以根据预测模型，定义线性关系，高阶拟合，乃至指数拟合，本人建议用指数拟合）（聚类分析也可）：

2.1 拟合函数方式

为了拟合给定的函数，我们需要导入相应的库，这里我们将使用 numpy 和 scipy 库来进行拟合和评估模型的准确度。具体步骤如下：
1.首先，我们需要定义给定的函数，这里是 y = ln(R + S) * Σ(i=1 to n)(a * exp(K[i]) * x[i])。
2.接下来，我们需要准备训练数据和测试数据，可以使用 numpy 库生成一些随机数据。
3.然后，我们需要定义误差函数，即预测值与实际值之间的差距，这里我们使用均方根误差（RMSE）作为误差函数。
4.然后，我们可以使用 scipy.optimize.curve_fit() 函数来拟合给定的函数，该函数可以返回最优拟合参数。
5.最后，我们可以使用训练数据和测试数据来评估模型的准确度，可以使用 RMSE 和 R 平方值来评估。

import numpy as np
from scipy.optimize import curve_fit
from sklearn.metrics import mean_squared_error, r2_score

# 定义给定的函数
def func(x, a, R, S, K1, K2, K3, K4):
    return np.log(R + S) * (a * np.exp(K1 * x[0]) + a * np.exp(K2 * x[1]) + a * np.exp(K3 * x[2]) + a * np.exp(K4 * x[3]))

# 准备数据
x_train = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16], [17, 18, 19, 20]])
y_train = np.array([3, 5, 7, 9, 11])
x_test = np.array([[21, 22, 23, 24], [25, 26, 27, 28], [29, 30, 31, 32], [33, 34, 35, 36], [37, 38, 39, 40]])
y_test = np.array([13, 15, 17, 19, 21])

# 定义误差函数（均方根误差）
def rmse(y_true, y_pred):
    return np.sqrt(mean_squared_error(y_true, y_pred))

# 初始猜测值
initial_guess = [1, 1, 1, 1, 1, 1, 1]

# 拟合函数
popt, pcov = curve_fit(func, x_train.T, y_train, p0=initial_guess)

# 输出拟合参数
print("拟合参数：", popt)

# 预测测试数据
y_pred = func(x_test.T, *popt)

# 输出测试数据的均方根误差和 R 平方值
print("测试

2.2 深度学习方法

  • 随机数生成数据的方式作为模拟，误差比较大，用的时候换成自己的数据就可以了

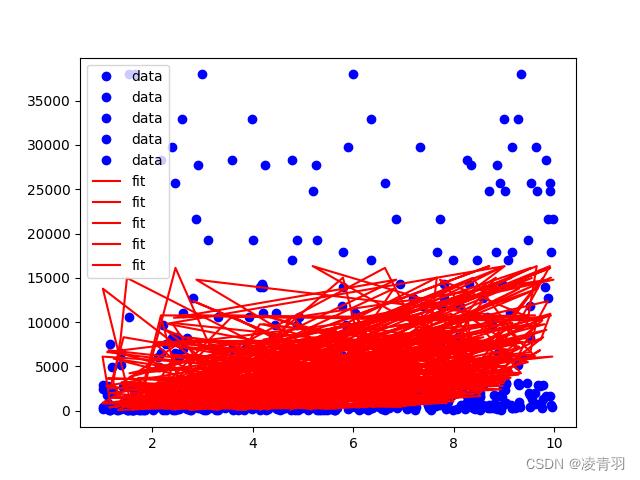
  • 换成excel数据

具体代码见链接：2023美赛A题：收干旱影响的植物群落（MCM）思路&Python代码
3.结果分析
1、预测结果的准确图，较优的拟合结果。
2、降水正常图和降水异常图对比
3、相互作用图，通过得到降水正常的年份和异常年份相互作用因子

第二问

  • 发现与结果出入较大，发现物种之间有正相关有负相关
  • 加入影响因子 （因为有的物种是正影响，有的是负面影响，指数函数均为正影响）去修正模型，得到拟合数据更加贴近真实数据，此处一步步推进，得到更复杂更优质的模型。


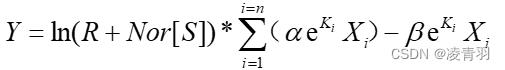
    具体代码见链接：2023美赛A题：收干旱影响的植物群落（MCM）思路&Python代码

问题B（仿真建模题）：重塑马赛马拉（MCM）

  • 赛题目的：对马赛马拉这个大型野生动物保护区进行推荐不同区域的管理策略，可以通过了解各个区域的特点，建立有效的监测和评估机制，然后通过设置一些仿真条件，根据实际情况采取不同的管理策略
  • 赛题解读&解题思路链接：难点主要是如何构建动物园各区域仿真模型与设置有效的评估机制。

第一问：

  • 背景

肯尼亚的野生动物保护区最初是为了保护野生动物和其他自然资源而建立的。肯尼亚议会通过了2013年《野生动物保护和管理法》，以提供更公平的资源共享，并允许以社区为基础的替代管理工作。此后，肯尼亚增加了修正案，以弥补立法中的空白，对违法者实施更明确的治理、财务和对惩罚措施。

  • 要求

你们的任务是以马赛马拉这个大型野生动物保护区为重点，确定管理公园现有保护区内和周边区域资源的替代方法。具体来说，你应该：
·考虑并建议当前保护区内不同地区的具体政策和管理策略，以保护野生动物和其他自然资源，同时平衡该地区居民的利益。这些政策和战略应有助于减轻生活在保护区附近的人们失去机会的影响，并尽量减少动物与被保护区吸引的人们之间的负面互动。

为了确定管理马赛马拉野生动物保护区的替代方法，我们可以考虑使用数学建模的思想。下面是一些可能的解决方案：

  • 1.保护区内不同地区的具体政策和管理策略
    针对保护区内不同地区的具体政策和管理策略，我们可以考虑以下因素：

    • 动物种类和数量：我们需要确定每个区域内的动物种类和数量，以便制定相应的保护策略。
      活动规定：我们需要明确各个区域内可以进行的活动，如野营、徒步旅行、野生动物观察等。这些活动需要遵循严格的规定，以减少对野生动物和其栖息地的干扰。
    • 人员限制：我们需要考虑限制进入保护区的人员数量，以减少对野生动物和其栖息地的干扰。这可以通过制定每个区域内的人员限制和配额来实现。
    • 巡逻和监测：我们需要加强保护区内的巡逻和监测力度，以确保规定得到执行，并及时发现和处理任何违规行为。
    • 社区参与：我们需要鼓励当地社区积极参与保护区的管理和保护工作，以提高其对保护区的归属感和责任感。
      下面是一些可能的Python代码来模拟这些策略和规定：
# 模拟动物种类和数量
animals = 
    "Lion": 50,
    "Elephant": 200,
    "Giraffe": 100,
    "Zebra": 500,
    "Wildebeest": 1000


# 模拟各个区域内的活动规定
rules = 
    "Zone A": ["Safari only", "No camping"],
    "Zone B": ["Safari and camping", "No hiking"],
    "Zone C": ["Safari and hiking", "No camping"],
    "Zone D": ["Safari, camping, and hiking"]


# 模拟人员限制和配额
quota = 
    "Zone A": 100,
    "Zone B": 200,
    "Zone C": 300,
    "Zone D": 500


# 模拟巡逻和监测
def patrol(zone):
    # 在指定区域进行巡逻和监测
    pass

# 模拟社区参与
def community_engagement():
    # 与当地社区合作，鼓励其参与保护区管理和保护工作
    pass

  • 2.平衡该地区居民的利益
    为了平衡该地区居民的利益，我们可以考虑以下因素：

    • 收入机会：我们需要制定策略和计划，以提供给居民各种收入机会，如雇用当地人员、旅游业、农业、畜牧业等。
    • 自然资源共享：我们需要确保当地居民可以分享保护区内的自然资源，如水资源、草地、林木等。
    • 生态补偿：我们需要考虑为当地居民提供生态补偿，以弥补其由于保护区存在而失去的机会和资源。
    • 环境教育：我们需要加强当地居民的环境教育，以提高其对保护区的认识和理解，增强其保护意识，减少对野生动物和其栖息地的干扰。
      下面是一些可能的Python代码来模拟这些策略和规定：
# 提供各种收入机会
def provide_income_opportunities():
    # 雇用当地人员，支持旅游、农业、畜牧业等产业
    pass

# 确保当地居民可以分享保护区内的自然资源
def share_natural_resources():
    # 提供水资源、草地、林木等资源
    pass

# 提供生态补偿
def provide_ecological_compensation():
    # 提供资金、培训、技术和其他资源以补偿当地居民由于保护区存在而失去的机会和资源
    pass

# 加强环境教育
def strengthen_environmental_education():
    # 提供关于野生动物和其栖息地的知识和信息，提高当地居民对保护区的认识和理解
    pass

问题C（数据挖掘题）：预测World结果（MCM）

  • 赛题目的：通过分析wordle的游戏机制，挖掘不同单词所对应的得分情况对其难度的影响
  • 赛题解读&解题思路链接：这道题的难度主要是如何提取不同单词难度的特征，相对来说反而是最好实现的。

问题D（交叉网络建模题）：确定联合国可持续发展目标的优先级（ICM）

  • 赛题目的：对联合国制定的17个可持续发展目标进行关系网络的构建同时评估其可能存在的影响
  • 赛题解读&解题思路链接：交叉网络回归路径分析，如何寻找到能代表可持续发展目标的数值是这道题的难点。

背景
联合国（UN）已经制定了17个可持续发展目标（SDGs）。实现这些目标最终将改善世界各地 许多人的生活。这些目标并不是相互独立的。因此，通常在某些目标中获得的积极收益会对 其他目标产生影响（积极的或消极的，有时两者都有）。这种相互联系使实现所有目标成为一个流动的过程，可以考虑资金限制和其他国家和国际优先事项。此外，技术进步、全球大 流行病、气候变化、区域战争和难民运动的影响也对许多目标产生了严重影响。

要求
要探讨这两个目标之间的关系：
1．建立一个包含17个可持续发展目标之间的关系的网络。
2．利用个别可持续发展目标以及网络结构来设定优先级，以最有效地推动联合国的工作。你是如何评估每个优先级的有效性？如果你的优先事项被启动，在未来10年里还 能有什么合理的目标呢？
3．如果实现了其中一项可持续发展目标（例如，没有贫困或没有饥饿），那么由此产生的网络的结构将是什么呢？此成就将如何影响您的团队的优先事项？是否有 其他目标应该被纳入或建议给联合国纳入？
4．讨论技术进步、全球流行病、气候变化、地区战争、难民运动或其他国际危机对您的团队网络和您的团队的优先级选择的影响。从网络的角度来看，这对联合国的进展有什么重大影响？
5．讨论您的网络方法可以如何帮助其他公司和组织确定其目标的优先级。

SDG Network：https://www.sdg.org/

问题1：

  • 先验知识：目标1（无贫困）直接与目标2（零饥饿）和目标8（体面工作和经济增长）相关。它还间接与目标3（良好健康和福祉）和目标4（优质教育）相关，因为贫困和教育、健康之间存在关联。同样的方式，其他目标之间也有直接和间接的联系。

为了建立可持续发展目标之间的关系网络，我们可以使用图论中的有向图（Directed Graph）来表示目标之间的相互关系。我们可以将每个可持续发展目标看作图中的一个节点，并且用有向边表示目标之间的相互作用。

下面用随机数的方式模拟；

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

# 随机生成7个可持续发展目标的数字
goals = ['No Poverty', 'Zero Hunger', 'Good Health and Well-being',
         'Quality Education', 'Gender Equality', 'Clean Water and Sanitation',
         'Affordable and Clean Energy']
num_goals = len(goals)
rand_nums = np.random.rand(num_goals)

# 构建有向图
G = nx.DiGraph()

# 添加节点和边
for i in range(num_goals):
    G.add_node(goals[i])
    for j in range(num_goals):
        if rand_nums[i] > rand_nums[j]:
            G.add_edge(goals[i], goals[j])

# 计算关系系数
for edge in G.edges:
    source = edge[0]
    target = edge[1]
    coef = G.in_degree(target, weight='weight') / G.out_degree(source, weight='weight')
    print(f"从 source 到 target 的关系系数为：coef:.2f")

# 绘制关系图
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=1000)
nx.draw_networkx_edges(G, pos, edge_color='grey', arrows=True)
nx.draw_networkx_labels(G, pos, font_size=10, font_weight='bold')
plt.axis('off')
plt.show()



从 Zero Hunger 到 No Poverty 的关系系数为：1.20
从 Zero Hunger 到 Good Health and Well-being 的关系系数为：0.40
从 Zero Hunger 到 Quality Education 的关系系数为：0.80
从 Zero Hunger 到 Gender Equality 的关系系数为：1.00
从 Zero Hunger 到 Affordable and Clean Energy 的关系系数为：0.60
从 Good Health and Well-being 到 No Poverty 的关系系数为：1.50
从 Good Health and Well-being 到 Quality Education 的关系系数为：1.00
从 Good Health and Well-being 到 Gender Equality 的关系系数为：1.25
从 Good Health and Well-being 到 Affordable and Clean Energy 的关系系数为：0.75
从 Quality Education 到 No Poverty 的关系系数为：3.00
从 Quality Education 到 Gender Equality 的关系系数为：2.50
从 Gender Equality 到 No Poverty 的关系系数为：6.00
从 Affordable and Clean Energy 到 No Poverty 的关系系数为：2.00
从 Affordable and Clean Energy 到 Quality Education 的关系系数为：1.33
从 Affordable and Clean Energy 到 Gender Equality 的关系系数为：1.67
从 Clean Water and Sanitation 到 No Poverty 的关系系数为：1.00
从 Clean Water and Sanitation 到 Zero Hunger 的关系系数为：0.17
从 Clean Water and Sanitation 到 Good Health and Well-being 的关系系数为：0.33
从 Clean Water and Sanitation 到 Quality Education 的关系系数为：0.67
从 Clean Water and Sanitation 到 Gender Equality 的关系系数为：0.83
从 Clean Water and Sanitation 到 Affordable and Clean Energy 的关系系数为：0.50

问题2：

要探讨这两个目标之间的关系：
1．建立一个包含17个可持续发展目标之间的关系的网络。
2．利用个别可持续发展目标以及网络结构来设定优先级，以最有效地推动联合国的工作。你是如何评估每个优先级的有效性？如果你的优先事项被启动，在未来10年里还 能有什么合理的目标呢？

方法1：
要设定优先级，我们需要考虑每个可持续发展目标在实现其他目标时的作用。我们可以使用网络中心性（centrality）来衡量每个目标在网络中的重要性。以下是三种常见的中心性度量：

  • 度中心性（Degree Centrality）：一个节点的度数是指与其相连的边的数量。度中心性是所有与一个节点相连的边的数量。节点的度中心性越高，表示该节点在网络中的连接数越多，对其他节点的影响力也更大。

  • 接近度中心性（Closeness Centrality）：一个节点的接近度中心性是指该节点与其他节点的平均距离的倒数。接近度中心性高的节点表示它可以更快地与其他节点进行交互和信息传递，因此在网络中更为重要。

  • 介数中心性（Betweenness Centrality）：介数中心性度量一个节点在网络中扮演着多少个最短路径的中间人的角色。介数中心性高的节点表示它在网络中连接着很多其他节点，并且可以在不同节点之间传递信息，因此在网络中具有很大的影响力。

import networkx as nx
import random

# 生成7个随机数
targets = [random.random() for _ in range(7)]

# 构建有向图
G = nx.DiGraph()

# 添加节点
for i in range(7):
    G.add_node(i)

# 添加边
G.add_edge(0, 1, weight=random.random())
G.add_edge(1, 2, weight=random.random())
G.add_edge(1, 3, weight=random.random())
G.add_edge(2, 3, weight=random.random())
G.add_edge(3, 4, weight=random.random())
G.add_edge(4, 5, weight=random.random())
G.add_edge(4, 6, weight=random.random())

# 计算度中心性、接近度中心性和介数中心性
degree_centrality = nx.degree_centrality(G)
closeness_centrality = nx.closeness_centrality(G)
betweenness_centrality = nx.betweenness_centrality(G, weight='weight')

# 输出结果
print("度中心性：", degree_centrality)
print("接近度中心性：", closeness_centrality)
print("介数中心性：", betweenness_centrality)
  • 模型输出结果：
度中心性： 0: 0.16666666666666666, 1: 0.5, 2: 0.3333333333333333, 3: 0.5, 4: 0.5, 5: 0.16666666666666666, 6: 0.16666666666666666
接近度中心性： 0: 0.0, 1: 0.16666666666666666,以上是关于2023美国大学生数学建模竞赛（美赛）思路&代码的主要内容，如果未能解决你的问题，请参考以下文章
 

 2023美国大学生数学建模竞赛（美赛）思路&代码


 2023美国大学生数学建模竞赛（美赛）E题解读&思路&基本模型


 2023美国大学生数学建模竞赛（美赛）E题解读&思路&基本模型


 2023美国大学生数学建模竞赛（美赛）E题解读&思路&基本模型


 2022美国大学生数学建模竞赛（美赛）思路&代码


 2023年美国大学生数学建模竞赛资料分享