机器学习--线性回归R语言

Posted 2023-01-18 豆芽炒粉丝

回归分析就是利用样本，产生拟合方程，从而进行预测。简而言之，就是你用你手头上的数据进行模型的训练，然后用你得到的模型对于新数据进行预测。

---

一元线性回归：

例子：

y<- c(61,57,58,40,90,35,68)#weight
x<-c(170,168,175,153,185,135,172) #height
plot(x,y)
z<- lm(y~x+1)#假设y=ax+b
lines(x,fitted(z))#添加拟合值对x的散点图并连线

coef(z)#求模型系数
formula(z)#提取模型公式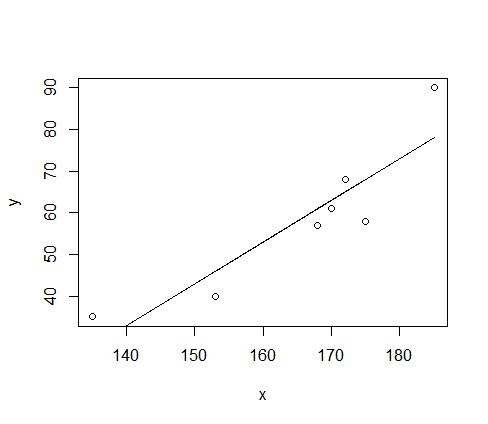

这是模型的概括
Call:
lm(formula = y ~ x + 1)

Residuals:
      1       2       3       4       5       6       7 
 -2.003  -4.002 -10.006  -5.992  11.988   7.019   2.996 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) -107.1018    34.8642  -3.072  0.02772 * 
x              1.0006     0.2099   4.768  0.00502 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 8.462 on 5 degrees of freedom
Multiple R-squared:  0.8197,    Adjusted R-squared:  0.7837 
F-statistic: 22.73 on 1 and 5 DF,  p-value: 0.005024

解读上述：

Residuals:
      1       2       3       4       5       6       7 
 -2.003  -4.002 -10.006  -5.992  11.988   7.019   2.996 

这是表示残差

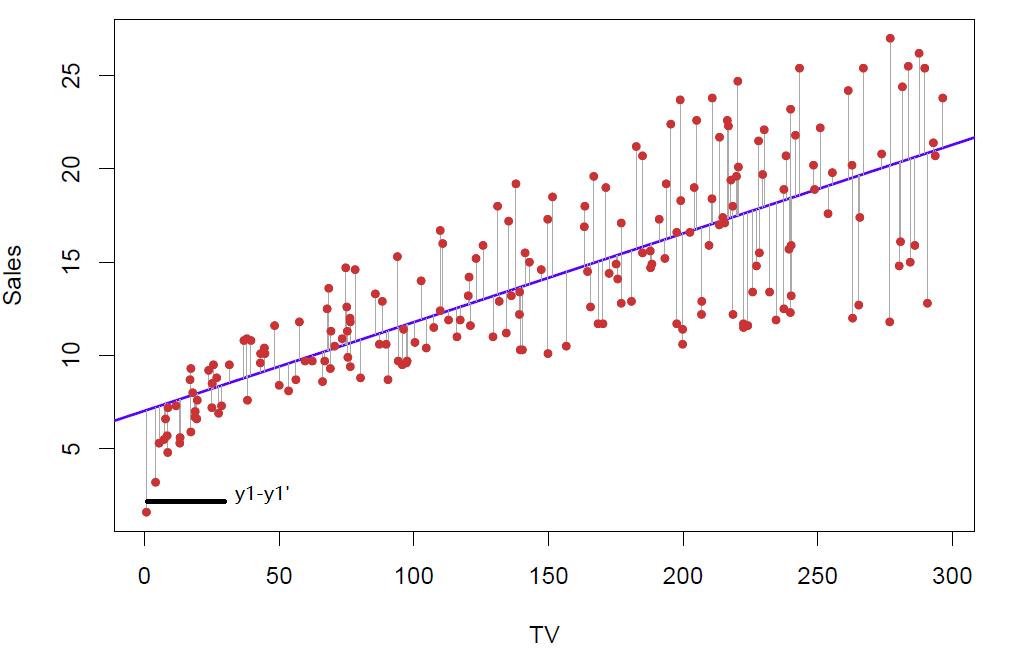
1 和 -2.003表示在第一个样本点的时候，残差为-2.003，也就是y1-y1’为-2.003

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) -107.1018    34.8642  -3.072  0.02772 * 
x              1.0006     0.2099   4.768  0.00502 **

第一列代表-107.1018代表的是截距，1.0006代表斜率
第二列：推算的系数的标准差
第三列：t值
第四列：p值，是一个验证假设是否成立的值。比如上面的身高体重模型，我假设身高height与weight无关系，也就是在原始的模型中呢，体重=常数+0*height，height前面系数为0，由此我们可以通过R算出一个统计量t值，Pr表示t值以外的面积，如果p>0.05我们就可以说拒绝原假设，也就是我们不能说height与weight无关系，为什么这个pr>0.05呢，而不是pr>0.01或者pr>0.0001呢，这个是关于一个t分布的面积问题吧，详细的百度谷歌吧。

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

显著性标记，* * * 极度显著，* * 高度显著，*显著，圆点不太显著，没有记号不显著
简而言之，*越多代表效果越好

(Intercept) -107.1018
x 1.0006 表示x的系数为1.0006，截距是-107.1018，也就是身高体重的一元线性模型方程是 y = 1.0006*x-107.1018

F-statistic: 22.73 on 1 and 5 DF,  p-value: 0.005024

这是对整个模型的一个检验，原理与上面的pr差不多，都属于假设检验。
用最小二乘法求解：

回归问题擅长于内推插值，而不擅长于外推归纳。所以在使用回归模型做预测时需要注意x的取值范围
内推值：即在图中存在的范围之内的点
外推值：即不在图中存在的范围之内的点
比如说刚刚的身高/体重模型，y = 1.0006*x-107.1018 ;我要预测一个170身高的人的体重，可以拟合比较准确，这个170就是内推值。
而身高比如说是20cm，那么体重是负数吗？显然不可能，那么这个20cm就是外推值

---

多元线性回归：

顾名思义，就是自变量多了，影响因素不唯一，比如说商品销售额，它可能跟广告投入、市场因素、节气变化等有关联(我自己臆想的)，所以这个时候，就会用到多元线性回归模型。
例子：
使用R语言内置swiss数据集，

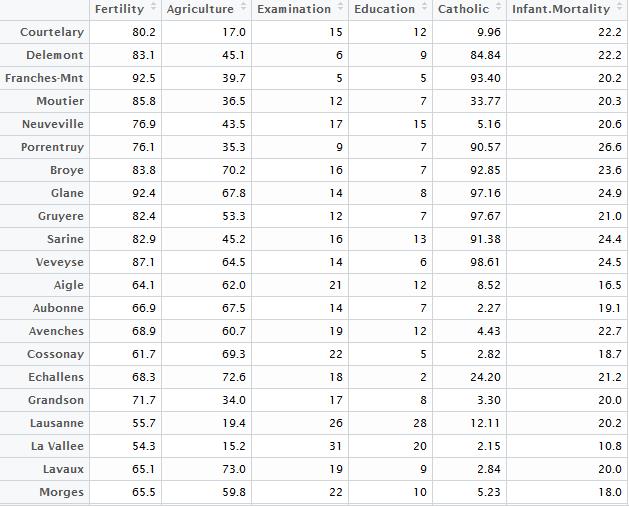
swiss数据集介绍

swiss.lm<- lm(Fertility~.,data=swiss)#Fertility是因变量，.表示因变量之外的所有列
summary(swiss.lm)
Call:
lm(formula = Fertility ~ ., data = swiss)

Residuals:
     Min       1Q   Median       3Q      Max 
-15.2743  -5.2617   0.5032   4.1198  15.3213 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)      66.91518   10.70604   6.250 1.91e-07 ***
Agriculture      -0.17211    0.07030  -2.448  0.01873 *  
Examination      -0.25801    0.25388  -1.016  0.31546    
Education        -0.87094    0.18303  -4.758 2.43e-05 ***
Catholic          0.10412    0.03526   2.953  0.00519 ** 
Infant.Mortality  1.07705    0.38172   2.822  0.00734 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.165 on 41 degrees of freedom
Multiple R-squared:  0.7067,    Adjusted R-squared:  0.671 
F-statistic: 19.76 on 5 and 41 DF,  p-value: 5.594e-10

注意了，我们通过观察，Multiple R-squared: 0.7067 这个数据还行，p-value: 5.594e-10 正确的可能性很高，然后看系数时发现后面的 “ * ” 号发现 Examination后面居然没有 “ * ” ，所以会存在隐忧，应该剔除examination
那么问题来了，变量多了，该怎么选择合适的变量呢？变量与变量之间是否存在共线性？
困难：
1. 选定变量（多元），因为有时候变量太多，有些对于模型是没有帮助甚至是倒忙，所以需要筛选。
2. 多重共线性：有些变量可以由其他变量推出来，若是存在，则会产生较大误差
3. 检验模型是否合理
逐步回归：多元线性回归选择变量的方法

1. 向前引入法：从一元回归开始，逐步增加变量，使指标达到最优
2. 向后剔除法：从全变量回归方程开始，逐步删去某个变量，使指标值达到最优为止
3. 逐步筛选法：综合上述两种方法
   在变量选取之前，有几个判断指标先介绍一下
   
   R语言有step()函数，

step(object, scope, scale = 0,
     direction = c("both", "backward", "forward"),
     trace = 1, keep = NULL, steps = 1000, k = 2, ...)
     具体信息可以help一下这个函数，下面我们使用step来做

direction：both表示综合两种方法，backward表示向后剔除，forward表示向前引入

step(object = swiss.lm,direction = "backward")#object表示模型，按照规范主要为lm（线性）或者glm（广义线性）模型
Start:  AIC=190.69
Fertility ~ Agriculture + Examination + Education + Catholic + 
    Infant.Mortality

                   Df Sum of Sq    RSS    AIC
- Examination       1     53.03 2158.1 189.86
<none>                          2105.0 190.69
- Agriculture       1    307.72 2412.8 195.10
- Infant.Mortality  1    408.75 2513.8 197.03
- Catholic          1    447.71 2552.8 197.75
- Education         1   1162.56 3267.6 209.36

Step:  AIC=189.86
Fertility ~ Agriculture + Education + Catholic + Infant.Mortality

                   Df Sum of Sq    RSS    AIC
<none>                          2158.1 189.86
- Agriculture       1    264.18 2422.2 193.29
- Infant.Mortality  1    409.81 2567.9 196.03
- Catholic          1    956.57 3114.6 205.10
- Education         1   2249.97 4408.0 221.43

Call:
lm(formula = Fertility ~ Agriculture + Education + Catholic + 
    Infant.Mortality, data = swiss)

Coefficients:
     (Intercept)       Agriculture         Education          Catholic  Infant.Mortality  
         62.1013           -0.1546           -0.9803            0.1247            1.0784  

分析：
从上面来看，初始状态下 Start: AIC=190.69,
模型：
Fertility ~ Agriculture + Examination + Education + Catholic + Infant.Mortality，
当剔除- Examination 1 53.03 2158.1 189.86 后，AIC=189.86
然后，step会继续进行剔除，然而，剔除任何变量AIC都不会变小，由此得到最终模型以及相关系数

Step:  AIC=189.86
Fertility ~ Agriculture + Education + Catholic + Infant.Mortality

                   Df Sum of Sq    RSS    AIC
<none>                          2158.1 189.86
- Agriculture       1    264.18 2422.2 193.29
- Infant.Mortality  1    409.81 2567.9 196.03
- Catholic          1    956.57 3114.6 205.10
- Education         1   2249.97 4408.0 221.43

Call:
lm(formula = Fertility ~ Agriculture + Education + Catholic +  Infant.Mortality, data = swiss)
Coefficients:
 (Intercept) Agriculture Education Catholic Infant.Mortality  
 62.1013     -0.1546    -0.9803      0.1247            1.0784  

方程：

Fertility = 62.1013*Agriculture-0.1546*Education-0.9803*Catholic+0.1247*Infant.Mortality

step函数both自己尝试，forward这个由于所有变量都已经在模型当中了，所以没法使用。
除step以外，R语言中还有两个函数可以做逐步回归，分别是drop1，add1
有时候，AIC准则并太适用，这里我们使用书中的内容来说明问题










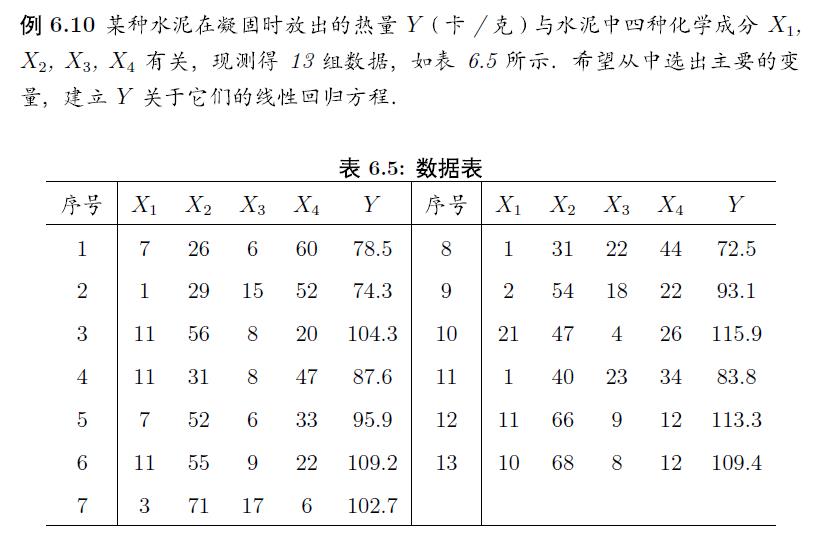
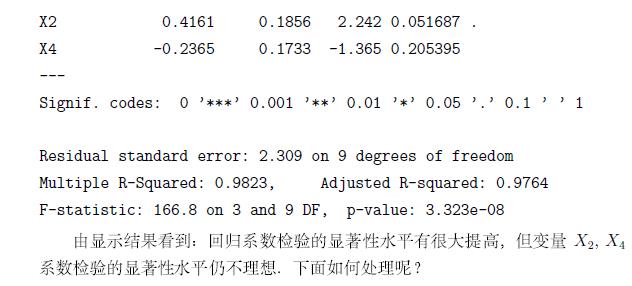
如有错误，请指出，谢谢！