如何理解拜占庭将军问题

Posted 2022-11-30 cuiran

拜占庭问题

拜占庭问题最早由 Leslie Lamport 等学者于 1982 年在论文《The Byzantine Generals Problem》中正式提出，是用来解释异步系统中共识问题的一个虚构模型。拜占庭是古代东罗马帝国的首都，由于地域宽广，守卫边境的多个将军（系统中的多个节点）需要通过信使来传递消息，达成某些一致决定。但由于将军中可能存在叛徒（系统中节点出错），这些叛徒将向不同的将军发送不同的消息，试图干扰共识的达成。这种情况十分类似于分布式系统中多个节点达成共识的问题。
拜占庭问题即讨论在此情况下，如何让忠诚的将军们能达成行动的一致。

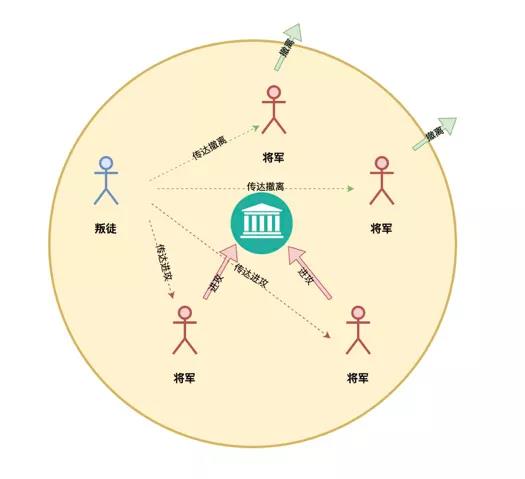
拜占庭问题（Byzantine Problem）又叫拜占庭将军（Byzantine Generals Problem）问题，讨论的是允许存在少数节点作恶（消息可能被伪造）场景下的如何达成共识问题。拜占庭容错（Byzantine Fault Tolerant，BFT）讨论的是容忍拜占庭错误的共识算法。

两将军问题

拜占庭问题之前，学术界就已经存在两将军问题的讨论（《Some constraints and tradeofis in the design of network communications》，1975 年）：两个将军要通过信使来达成进攻还是撤退的约定，但信使可能迷路或被敌军阻拦（消息丢失或伪造），如何达成一致？根据 FLP 不可能原理，这个问题无通用解。
###拜占庭问题的解决
拜占庭问题，假设节点总数是N，叛徒将军数为F，则当 N 》= 3F+1 时，问题才有解，共识才能达成，这就是Byzantine Fault Tolerant（BFT）算法。那如何快速理解呢？可以通过以下两种方式来进一步理解！

快速理解一

假设将军总数3，叛徒将军数1.我们分别从提案人是叛徒和不是叛徒两个角度去做分析。

提案人不是叛徒 ，提案人发送一个提案，叛徒收到后，回复不同的命令，对于第三个将军就收到两个相反的消息，也无法判断出谁是叛徒，系统无法达成一致。如图所示：

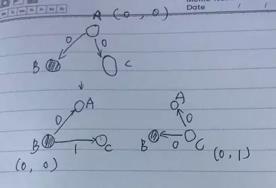
提案人是叛徒，发送两个相反的提案给另外两个，另外两个收到两个相反的消息，无法判断究竟谁是叛徒，系统无法达成一致。如图所示：

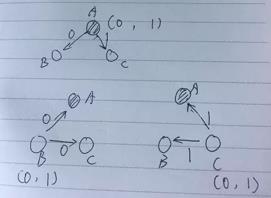
快速理解二

假设将军总数4，叛徒将军数1.我们还是分别从提案人是叛徒和不是叛徒两个角度去做分析。

提案人不是叛徒，提案人发送一个提案，叛徒同样作恶，但收到的消息结果，能很容易就找出哪个节点是叛徒。从而快速达成共识。如图所示：

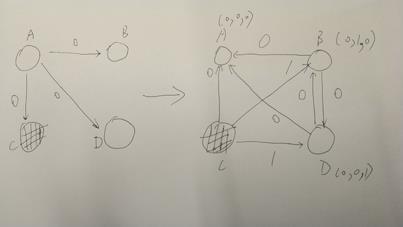
提案人是叛徒，发送不同的提案给不同的节点，但其他三个节点之间进行两两互相通信后，他们自己也能达成一个共识。如图所示:

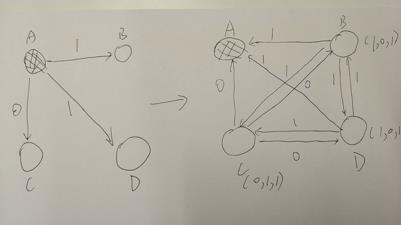
Leslie Lamport证明，当叛徒不超过1/3时，存在有效的算法，不论叛徒如何折腾，忠诚的将军们总能达成共识。当叛徒超过三分之一时，则无法保证一定能达成一致性。

Byzantine Fault Tolerant算法

面向拜占庭将军问题的容错算法，解决的是网络通信可靠，但节点可能故障情况下的一致性达成。

最早由Castro和Liskov在1999年提出的Practical Byzantine Fault Tolerant（PBFT）是第一个得到广泛应用的BFT算法。只要系统有2/3的节点是正常工作的，则可以保证一致性。

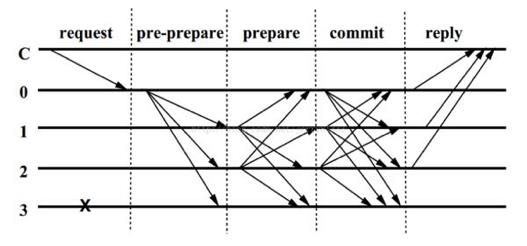
PBFT算法包括三个阶段来达成共识：Pre-Prepare，Prepare和Commit。如下图所示：

• Request：请求端C发送请求到主节点，这里是0节点；

• Pre-Prepare：节点0收到C的请求后进行广播，扩散至123；

• Prepare：123节点收到后记录并再次广播，1->023，2->013，3因为宕机无法广播；（这一步是为了防止主节点给不同从节点发送不同的请求）

• Commit：0123节点在Prepare阶段，若收到超过一定数量（2F，实际使用中，F为可以容忍的拜占庭节点个数）的相同请求，则进入Commit阶段，广播Commit请求；

• Reply：0123节点在Commit阶段，若其中有一个收到超过一定数量（2F+1）的相同请求，则对C进行反馈；

根据上述流程，在 N ≥ 3F + 1 的情況下一致性是可能解決，N为总计算机数，F为有问题的计算机总数。