读书笔记2|深度学习入门——基于python的理论与实现

Posted 2022-10-10 程序媛一枚~

深度学习入门：基于Python的理论与实现》高清中文版.pdf

1. python基础，numpy，matplotlib

Batch Normalization、Dropout、Adam

图像识别，自然语言处理，语音识别。

不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之

一维数组称为向量，二维数组称为矩阵，三维或以上数组称为张量（tensor）/多维数组。

broadcast广播

《Python 语言及其应用》这是一本详细介绍从 Python 编程的基础到应用的实践性的入门书。关于NumPy，《利用 Python 进行数据分析》

X = X.flatten() # 将 X 转换为一维数组
print(X)
[51 55 14 19 0 4]
X[np.array([0, 2, 4])] # 获取索引为 0、2、4 的元素
array([51, 14, 0])

Adam：进行超参数的“偏置校正”也是 Adam 的特征，梯度下降的优化方法——Momentum 参照小球在碗中滚动的物理规则进行移动，AdaGrad 为参数的每个元素适当地调整更新步伐，使得函数的取值高效地向着最小值移动。Adam融合了这俩点。

2. 感知机perception指人工神经元或者朴素感知机

与门 and gate 1 & 1 = 1
与非门 NAND Gate
或门
异或门 XOR Gate（1 & 0 = 1， 0 & 1 = 1）

与门、或门单层感知机；
异或门2层感知机；
多层感知机（multi-layered perception）

偏置，权重

3. 神经网络

输入层，输出层，中间层/隐藏层；
激活函数（activation function）
激活函数是连接感知机和神经网络的桥梁。
朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数 A 的模型。“多层感知机”是指神经网络，即使用 sigmoid函数（后述）等平滑的激活函数的多层网络。
sigmoid函数（sigmoid function）
ReLU（Rectified Linear Unit）函数
矩阵（matrix）行（row）列（col）

np.ndim – 维度
a.flatten() 铺平
a = a > 0 得到boolean的数组
a = a[a > 0] 返回大于0的值的下标对应的数据

np.dot 点积， MN NP — MP
行列，abcd efgh
22
[[ae+bg, af+bh],
[ce+dg],[cf+d*h]]

推理处理，也称为前向传播（forward propagation）

normalize正规化，如把像素由0_{255正规化到0}1.0；还有将数据的整体分布形状均匀化的方法，即数据白化（whitening）；
accuracy 准确度
pre-processing 预处理

PIL（Python Image Library）用于图像显示
Python 有 pickle 这个便利功能。可以将程序运行中的对象保存为文件。如果加载保存过的 pickle 文件，可以立刻复原之前程序运行中的对象。 用于读入 MNIST 数据集的 load_mnist() 函数内
部也使用了 pickle 功能（在第 2 次及以后读入时）。利用 pickle 功能，可以高效地完成 MNIST 数据的准备工作。
batch批

矩阵的第 0 维是列方向，第 1 维是行方向
Numpy多维数组计算
机器学习的问题大体上可以分为回归问题和分类问题。
关于输出层的激活函数，回归问题中一般用恒等函数，分类问题中一般用 softmax 函数。
Softmax 层将输入值正规化（将输出值的和调整为 1）之后再输出。
softmax 函数称为 softmax 层，交叉熵误差称为 Cross Entropy Error 层，两 者 的 组 合 称 为 Softmax-with-Loss 层。

4. 神经网络的学习

如何识别数字5：从数据中学习，从图像中提取特征量，再用机器学习技术学习这些特征量的模式。这里所说的 “特征量”是指可以从输入数据（输入图像）中准确地提取本质数据（重要的数据）的转换器。图像的特征量通常表示为向量的形式。 在计算机视觉领域，常用的特征量包括SIFT、SURF 和 HOG 等。使用这些特征量将图像数据转换为向量，然后对转换后的向量使用机器学习中的 SVM、KNN 等分类器进行学习。

深度学习有时也称为端到端机器学习（end-to-end machine learning）。这里所说的端到端是指从一端到另一端的意思，也就是从原始数据（输入）中获得目标结果（输出）的意思。

将数据分为训练数据和测试数据，以评估模型的泛化能力。测试数据也可称之为监督数据；
训练模型的终极目标是泛化能力。只对某个数据集过度拟合的状态称为过拟合（over fitting）。避免过拟合也是机器学习的一个重要课题。

神经网络的学习通过某个指标表示现在的状态。然后，以这个指标为基准，寻找最优权重参数。该指标称为损失函数（loss function）。这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。最有名的是均方误差（mean squared error）。

将正确解标签表示为 1，其他标签表示为 0 的表示方法称为 one-hot 表示。

除了均方误差之外，交叉熵误差（cross entropy error）也经常被用作损失函数。交叉熵误差如下：

神经网络的学习是从训练数据中选出一批数据（称为 mini-batch, 小批量），然后对每个 mini-batch 进行学习。比如，从 60000 个训练数据中随机选择 100 笔，再用这 100 笔数据进行学习。这种学习方式称为 mini-batch 学习。即用随机选择的小批量数据（mini-batch）作为全体训练数据的近似值。

• np.random.choice() 可以从指定的数字中随机选择想要的数字。比如np.random.choice(60000, 10) 会从 0 到 59999 之间随机选择 10 个数字。
• np.zeros_like(x) 会生成一个形状和 x 相同、所有元素都为 0 的数组。

数值微分 A 的英文 numerical differentiation
舍入误差（rounding error）

利用微小的差分求导数的过程称为数值微分（numerical differentiation）。而基于数学式的推导求导数的过程，则用“解析性”（analytic）一词，称为“解析性求解”或者“解析性求导”。

梯度（gradient）

函数的极小值、最小值以及被称为鞍点（saddle point）的地方，梯度为 0。极小值是局部最小值，也就是限定在某个范围内的最小值。鞍点是从某个方向上看是极大值，从另一个方向上看则是极小值的点。虽然梯度法是要寻找梯度为 0 的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点）。此外，当函数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区，陷入被称为“学习高原”的无法前进的停滞期。
通过不断地沿梯度方向前进，逐渐减小函数值的过程就是梯度法（gradient method）。梯度法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。

寻找最小值的梯度法称为梯度下降法（gradient descent method），
寻找最大值的梯度法称为梯度上升法（gradient ascent method）。

学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。 一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。

数据是随机选择的 mini batch 数据，所以又称为随机梯度下降法（stochastic gradient descent）。“随机”指的是“随机选择的”的意思，因此，随机梯度下降法是“对随机选择的数据进行的梯度下降法”。 深度学习的很多框架中，随机梯度下降法一般由一个名为 SGD 的函数来实现。SGD 来源于随机梯度下降法的英文名称的首字母。

epoch 是一个单位。一个 epoch 表示学习中所有训练数据均被使用过一次时的更新次数。一个纪元，如总共10000数据，mini-batch=100，则100个batch后所有的数据就都被训练一次，即一个纪元。每经过一个 epoch 就记录一次训练数据的识别精度。

• 机器学习中使用的数据集分为训练数据和测试数据。
• 神经网络用训练数据进行学习，并用测试数据评价学习到的模型的 泛化能力。
• 神经网络的学习以损失函数为指标，更新权重参数，以使损失函数 的值减小。
• 利用某个给定的微小值的差分求导数的过程，称为数值微分。
• 利用数值微分，可以计算权重参数的梯度。
• 数值微分虽然费时间，但是实现起来很简单。下一章中要实现的稍微复杂一些的误差反向传播法可以高速地计算梯度。

5. 误差反向传播法

计算图（computational graph），计算图将计算过程用图形表示出来。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。

正向传播 forward propagation
反向传播 back propagation

计算图的优点是，可以通过正向传播和反向传播高效地计算各个变量的导数值。
链式法则（chain rule）

激活函数 ReLU（Rectified Linear Unit） >0, 输出1 <=0输出0
ReLU 层的作用就像电路中的开关一样。正向传播时，有电流通过的话，就将开关设为 ON；没有电流通过的话，就将开关设为 OFF。反向传播时，开关为 ON 的话，电流会直接通过；开关为 OFF 的话，则不会有电流通过。

sigmoid 函数：
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”A。因此，这里将进行仿射变换的处理实现为“Affine 层”，用np.dot实现；

神经网络中进行的处理有推理（inference）和学习两个阶段。神经网络的推理通常不使用 Softmax 层。 比如图 5-28 的网络进行推理时，会将最后一个 Affine 层的输出作为识别结果。神经网络中未被正规化的输出结果（图 5-28 中 Softmax 层前面的 Affine 层的输出）有时被称为“得分”。 也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要 Softmax 层。不过，神经网络的学习阶段则需要 Softmax 层。

• 计算图的节点是由局部计算构成的。局部计算构成全局计算。
• 计算图的正向传播进行一般的计算。通过计算图的反向传播，可以计算各个节点的导数。
• 通过将神经网络的组成元素实现为层，可以高效地计算梯度（反向传 播法）。
• 通过比较数值微分和误差反向传播法的结果，可以确认误差反向传 播法的实现是否正确（梯度确认）。

6. 与学习相关的方法

神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization）

为了找到最优参数，将参数的梯度（导数）作为了线索。使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法（stochastic gradient descent），简称 SGD。
SGD 是朝着梯度方向只前进一定距离的简单方法。

如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。需要比单纯朝梯度方向前进的 SGD 更聪明的方法。SGD 低效的根本原因是，梯度的方向并没有指向最小值的方向。

在神经网络的学习中，学习率（数学式中记为 η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。

梯度下降法的几种方法：
问题不同，超参数设置不同，很难说那种方法最优。一般而言，与 SGD 相比，其他 3 种方法可以学习得更快，有时最终的识别精度也更高。

抑制过拟合、提高泛化能力的技巧——权值衰减（weight decay）。简单地说，权值衰减就是一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。

偏向 0 和 1 的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。

各层的激活值的分布都要求有适当的广度。为什么呢？因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习。反过来，如果传递的是有所偏向的数据，就会出现梯度消失或者“表现力受限”的问题，导致学习可能无法顺利进行。

Batch Norm 的思路是调整各层的激活值分布使其拥有适当的广度。为此，要向神经网络中插入对数据分布进行正规化的层，即 Batch Normalization 层（下文简称 Batch Norm 层），有以下惊人的优点：
• 可以使学习快速进行（可以增大学习率）。
• 不那么依赖初始值（对于初始值不用那么神经质）。
• 抑制过拟合（降低 Dropout 等的必要性）。

过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机
器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据，也希望模型可以进行正确的识别。

发生过拟合的原因，主要有以下两个:
• 模型拥有大量参数、表现力强。
• 训练数据少。

权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

L2 范数相当于各个元素的平方和。 用数学式表示的话，假设有权重W = (w1, w2, . . . , wn)，则 L2 范数可用 计算出来。除了 L2 范数，还有 L1 范数、L ∞范数等。L1 范数是各个元素的绝对值之和，相当于 |w1| + |w2| + . . . + |w n|。L∞范数也称为Max 范数，相当于各个元素的绝对值中最大的那一个。 L2 范数、L1范数、L∞范数都可以用作正则化项，它们各有各的特点。

如上图有抑制作用，并且准确度没达到100%，虽然测试/训练集依然有差距，但差别没那么大了。

神经网络的学习目的是减小损失函数的值。例如为损失函数加上权重的平方范数（L2 范数）。但如果网络的模型变得很复杂，只用权值衰减就难以应对了。在这种情况下，经常会使用 Dropout方法。

Dropout 是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递。然后，测试时虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

神经网络中，除了权重和偏置等参数，超参数（hyper-parameter）也经常出现。这里所说的超参数是指，比如各层的神经元数量、batch 大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值，模型的性能就会很差。

调整超参数时，必须使用超参数专用的确认数据。用于调整超参数的数据，一般称为验证数据（validation data）。使用这个验证数据来评估超参数的好坏。

训练数据用于参数（权重和偏置）的学习，验证数据用于超参数的性能评估。为了确认泛化能力，要在最后使用（比较理想的是只用一次）测试数据。

对数尺度（log scale）在超参数的最优化中，减少学习的 epoch，缩短一次评估所需的时间是一个不错的办法。在超参数的最优化中，如果需要更精炼的方法，可以使用贝叶斯最优化（Bayesian optimization）。贝叶斯最优化运用以贝叶斯定理为中心的数学理论，能够更加严密、高效地进行最优化。

• 权重初始值的赋值方法对进行正确的学习非常重要。
• 作为权重初始值，Xavier 初始值、He 初始值等比较有效。
• 通过使用Batch Normalization，可以加速学习，并且对初始值变得健壮。
• 抑制过拟合的正则化技术有权值衰减、Dropout 等。
• 逐渐缩小“好值”存在的范围是搜索超参数的一个有效方法。

7. 卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）
CNN 中新出现了卷积层（Convolution 层）和池化层（Pooling 层），卷积神经网络也像神经网络一样，可以通过组装层来实现。
神经网络中，相邻层的所有神经元之间都有连接，这称为全连接（fully-connected）。另外用 Affine 层实现了全连接层。全连接的神经网络中，Affine 层后面跟着激活函数 ReLU层（或者 Sigmoid 层）。这里堆叠了 4 层“Affine-ReLU”组合，然后第 5 层是
Affine 层，最后由 Softmax 层输出最终结果（概率）。

神经网络 & 卷积神经网络对比：

CNN 中，有 时 将 卷 积 层 的 输 入 输 出 数 据 称 为 特 征 图（feature map）。其中卷积层的输入数据称为输入特征图（input feature map），输出数据称为输出特征图（output feature map）

填充（padding）卷积运算的填充处理：向输入数据的周围填入 0（图中用虚线表示填充，并省略了填充的内容“0”。使用填充主要是为了调整输出的大小。 因为如果每次进行卷积运算都会缩小空间，那么在某个时刻输出大小就有可能变为 1，导致无法再应用卷积运算。为了避免出现这样的情况，就要使用填充。在刚才的例子中，将填充的幅度设为 1，那么相对于输入大小 (4, 4)，输出大小也保持为原来的 (4, 4)。因此，卷积运算就可以在保持空间大小不变的情况下将数据传给下一层。

应用滤波器的位置间隔称为步幅（stride）。增大步幅后，输出大小会变小。而增大填充后，输出大小会变大。

池化层：Max 池化是从目标区域中取出最大值，Average 池化则是计算目标区域的平均值。在图像识别领域，主要使用 Max 池化。

池化层特征：

• 没有要学习的参数
  池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。
• 通道数不发生变化
  经过池化运算，输入数据和输出数据的通道数不会发生变化。
• 对微小的位置变化具有鲁棒性（健壮）
  输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对
  输入数据的微小偏差具有鲁棒性。

im2col 是一个函数，将输入数据展开以适合滤波器（权重）。对 3 维的输入数据应用 im2col 后，数据转换为 2 维矩阵（正确地讲，是把包含批数量的 4 维数据转换成了 2 维数据）。
im2col 这个名称是“image to column”的缩写，翻译过来就是“从图 像 到 矩 阵”的 意 思。Caffe、Chainer 等 深 度 学 习 框 架 中 有 名 为im2col 的函数，并且在卷积层的实现中，都使用了 im2col。

卷积层的初始化方法将滤波器（权重）、偏置、步幅、填充作为参数接收。滤 波 器 是 (FN, C, FH, FW) 的 4 维 形 状。另 外，FN、C、FH、FW 分 别 是 Filter Number（滤波器数量）、Channel、Filter Height、Filter Width 的缩写。

reshape()，通过在 reshape 时指定为 -1，reshape 函数会自动计算 -1 维度上的元素个数，以使多维数组的元素个数前后一致。比如，(10, 3, 5, 5) 形状的数组的元素个数共有 750 个，指定 reshape(10,-1) 后，就会转换成 (10, 75) 形状的数组。

transpose() 会更改多维数组的轴的顺序。

最 大 值 的 计 算 可 以 使 用 NumPy 的 np.max 方 法。np.max 可 以 指 定axis 参数，并在这个参数指定的各个轴方向上求最大值。比如，如果写成 np.max(x, axis=1)，就可以在输入 x 的第 1 维的各个轴方向上求最大值。

卷积层和池化层是图像识别中必备的模块。CNN 可以有效读取图像中的某种特性，在手写数字识别中，还可以实现高精度的识别。

AlexNet 网络结构堆叠了多层卷积层和池化层，最后经过全连接层输出结果。

随着层次加深，神经元从简单的形状向“高级”信息变化。换句话说，就像我们理解东西的“含义”一样，响应的对象在逐渐变化。

CNN很多，最经典的俩个CNN——其中特别重要的两个网络，一个是在 1998 年首次被提出的 CNN 元祖 LeNet，另一个是在深度学习受到关注的 2012 年被提出的 AlexNet。

• LeNet
  LeNet 在 1998 年被提出，是进行手写数字识别的网络。它有连续的卷积层和池化层（正确地讲，是只“抽选元素”的子采样层），最后经全连接层输出结果。
  LeNet 中使用 sigmoid 函数，而现在的 CNN 中主要使用 ReLU 函数。此外，原始的 LeNet 中使用子采样（subsampling）缩小中间数据的大小，而现在的 CNN 中 Max 池化是主流。

• AlexNet
  AlexNet 是引发深度学习热潮的导火线，不过它的网络结构和 LeNet 基本上没有什么不同。AlexNet 叠有多个卷积层和池化层，最后经由全连接层输出结果。AlexNet的激活函数使用 ReLU；使用进行局部正规化的 LRN（Local Response Normalization）层；使用 Dropout层。

大数据和 GPU 已成为深度学习发展的巨大的原动力。

• CNN 在此前的全连接层的网络中新增了卷积层和池化层。
• 使用 im2col 函数可以简单、高效地实现卷积层和池化层。
• 通过 CNN 的可视化，可知随着层次变深，提取的信息愈加高级。
• LeNet 和 AlexNet 是 CNN 的代表性网络。
• 在深度学习的发展中，大数据和 GPU 做出了很大的贡献。

8. 深度学习

深度学习是加深了层的深度神经网络。集成学习、学习率衰减、Data Augmentation（数据扩充）、加深层等都有助于提高识别精度。 尤其是Data Augmentation，虽然方法很简单，但在提高识别精度上效果显著。

Data Augmentation 基于算法“人为地”扩充输入图像（训练图像）。具体地说，对于输入图像，通过施加旋转、垂直或水平方向上的移动，裁剪图像的“crop 处理”、将图像左右翻转的“flip处理”等微小变化。对于一般的图像，施加亮度等外观上的变化、放大缩小等尺度上的变化也是有效的。这样能增加训练集图像的数量。这在数据集的图像数量有限时尤其有效。

叠加小型滤波器来加深网络的好处是可以减少参数的数量，扩大感受野（receptive field，给神经元施加变化的某个局部空间区域）。 并且，通过叠加层，将 ReLU 等激活函数夹在卷积层的中间，进一步提高了网络的表现力。这是因为向网络添加了基于激活函数的“非线性”表现力，通过非线性函数的叠加，可以表现更加复杂的东西。

层越深，识别性能也越高。

• 加深层的其中一个好处就是可以减少网络的参数数量。与没有加深层的网络相比，加深了层的网络可以用更少的参数达到同等水平（或者更强）的表现力。
• 加深层的另一个好处就是使学习更加高效。与没有加深层的网络相比，通过加深层，可以减少学习数据，从而高效地进行学习。 通过加深层，可以将各层要学习的问题分解成容易解决的简单问题，从而可以进行高效的学习。

CNN 的卷积层会分层次地提取信息。具体地说，在前面的卷积层中，神经元会对边缘等简单的形状有响应，随着层的加深，开始对纹理、物体部件等更加复杂的东西有响应。

深度学习的小历史：
一般认为，现在深度学习之所以受到大量关注，其契机是 2012 年举办的大规模图像识别大赛 ILSVRC（ImageNet Large Scale Visual Recognition Challenge）。 在那年的比赛中，基于深度学习的方法（通称 AlexNet）以压倒
性的优势胜出，彻底颠覆了以往的图像识别方法。

ImageNet
ImageNet是拥有超过 100 万张图像的数据集。它包含了各种各样的图像，并且每张图像都被关联了标签（类别名）。每年都会举办使用这个巨大数据集的 ILSVRC 图像识别大赛。其中之一是“类别分类”（classification），在该项目中会进行 1000 个类别的分类，比试识别精度。
2012 年的 AlexNet 大幅降低了错误识别率。 并且此后基于深度学习的方法不断在提升识别精度。特别是 2015 年的 ResNet（一个超过 150 层的深度网络）将错误识别率降低到了 3.5%。据说这个结果甚至超过了普通人的识别能力。 这些年深度学习取得了不斐的成绩，其中 VGG、GoogLeNet、ResNet已广为人知。

• VGG
  VGG 是由卷积层和池化层构成的基础的 CNN。它的特点在于将有权重的层（卷积层或者全连接层）叠加至 16 层（或者 19 层），具备了深度（根据层的深度，有时也称为“VGG16”或“VGG19”）。
  VGG 中需要注意的地方是，基于 3×3 的小型滤波器的卷积层的运算是连续进行的。重复进行“卷积层重叠 2 次到 4 次，再通过池化层将大小减半”的处理，最后经由全连接层输出结果。
  

VGG 在 2014 年的比赛中最终获得了第 2 名的成绩（下一节介绍的GoogleNet 是 2014 年的第 1 名）。虽然在性能上不及 GoogleNet，但因为 VGG 结构简单，应用性强，所以很多技术人员都喜欢使用基于VGG 的网络。

• GoogLeNet
  GoogLeNet 的特征是，网络不仅在纵向上有深度，在横向上也有深度（广度）。
  GoogLeNet 在横向上有“宽度”，这称为“Inception 结构”，Inception 结构使用了多个大小不同的滤波器（和池化），最后再合并它们的结果。 GoogLeNet 的特征就是将这个 Inception 结构用作一个构件（构成元素）。此外，在 GoogLeNet 中，很多地方都使用了大小为1 × 1 的滤波器的卷积层。这个 1 × 1 的卷积运算通过在通道方向上减小大小，有助于减少参数和实现高速化处理。

• ResNet
  ResNet是微软团队开发的网络。它的特征在于具有比以前的网络更深的结构。
  我们已经知道加深层对于提升性能很重要。但是，在深度学习中，过度加深层的话，很多情况下学习将不能顺利进行，导致最终性能不佳。ResNet 中，为了解决这类问题，导入了“快捷结构”（也称为“捷径”或“小路”）。导入这个快捷结构后，就可以随着层的加深而不断提高性能了（当然，层的加深也是有限度的）。
  快捷结构横跨（跳过）了输入数据的卷积层，将输入 x 合计到输出。导致加深层能提升性能。
  通过快捷结构，反向传播时信号可以无衰减地传递。
  ResNet 以前面介绍过的 VGG 网络为基础，引入快捷结构以加深层。

实践中经常会灵活应用使用 ImageNet 这个巨大的数据集学习到的权重数据，这称为迁移学习，将学习完的权重（的一部分）复制到其他神经网络，进行再学习（fine tuning）。比如，准备一个和 VGG 相同结构的网络，把学习完的权重作为初始值，以新数据集为对象，进行再学习。迁移学习在手头数据集较少时非常有效。

• 深度学习的高速化
  从CPU到GPU。大多数深度学习的框架都支持GPU（Graphics Processing Unit），可以高速地处理大量的运算。 另外，最近的框架也开始支持多个 GPU 或多台机器上的分布式学习。

如何高速、高效地进行卷积层中的运算是深度学习的一大课题。
深度学习的高速化的主要课题就变成了如何高速、高效地进行大量的乘积累加运算。

• 基于 GPU 的高速化
  GPU 原本是作为图像专用的显卡使用的，但最近不仅用于图像处理，也用于通用的数值计算。由于 GPU 可以高速地进行并行数值计算，因此GPU 计算的目标就是将这种压倒性的计算能力用于各种用途。所谓 GPU 计算，是指基于 GPU 进行通用的数值计算的操作。
  深度学习中需要进行大量的乘积累加运算（或者大型矩阵的乘积运算）。这种大量的并行运算正是 GPU 所擅长的（反过来说，CPU 比较擅长连续的、复杂的计算）。 因此，与使用单个 CPU 相比，使用 GPU 进行深度学习的运算
  可以达到惊人的高速化。
  使用CPU43天，GPU7天，优化后的cuDNN可以进一步缩短时间。

GPU 主要由 NVIDIA 和 AMD 两家公司提供。 虽然两家的 GPU 都可以用于通用的数值计算，但与深度学习比较“亲近”的是 NVIDIA 的 GPU。 实际上，大多数深度学习框架只受益于 NVIDIA 的 GPU。这是因为深度学习的框架中使用了 NVIDIA 提供的 CUDA 这个面向 GPU 计算的综合开发环境。

通过 im2col 可以将卷积层进行的运算转换为大型矩阵的乘积。这个im2col 方式的实现对 GPU 来说是非常方便的实现方式。这是因为，相比按小规模的单位进行计算，GPU 更擅长计算大规模的汇总好的数据。也就是说，通过基于 im2col 以大型矩阵的乘积的方式汇总计算，更容易发挥出 GPU 的能力。

• 分布式学习
  考虑在多个 GPU 或者多台机器上进行分布式计算。 现在的深度学习框架中，出现了好几个支持多 GPU 或者多机器的分布式学习的框架。其中，Google 的TensorFlow、微软的 CNTK（Computational Network Toolki）在开发过程中高度重视分布式学习。以大型数据中心的低延迟·高吞吐网络作为支撑，基于这些框架的分布式学习呈现出惊人的效果。
  随着 GPU 个数的增加，学习速度也在提高。与使用 1 个 GPU 时相比，使用100 个 GPU（设置在多台机器上，共 100 个）似乎可以实现 56 倍的高速化！这意味着之前花费 7 天的学习只要 3 个小时就能完成，充分说明了分布式学习惊人的效果。
  关于分布式学习，“如何进行分布式计算”是一个非常难的课题。它包含了机器间的通信、数据的同步等多个无法轻易解决的问题。可以交给分布式框架如TensorFlow等框架去解决。

深度学习的应用案例：物体检测，物体识别，图像分割，图像标题的生成。

• 物体检测
  物体检测是从图像中确定物体的位置，并进行分类的问题。
  物体检测是比物体识别更难的问题。物体识别是以整个图像为对象的，但是物体检测需要从图像中确定类别的位置，而且还有可能存在多个物体。
  在使用 CNN 进行物体检测的方法中，有一个叫作 R-CNN的有名的方法。下图 显示了 R-CNN 的处理流。
  
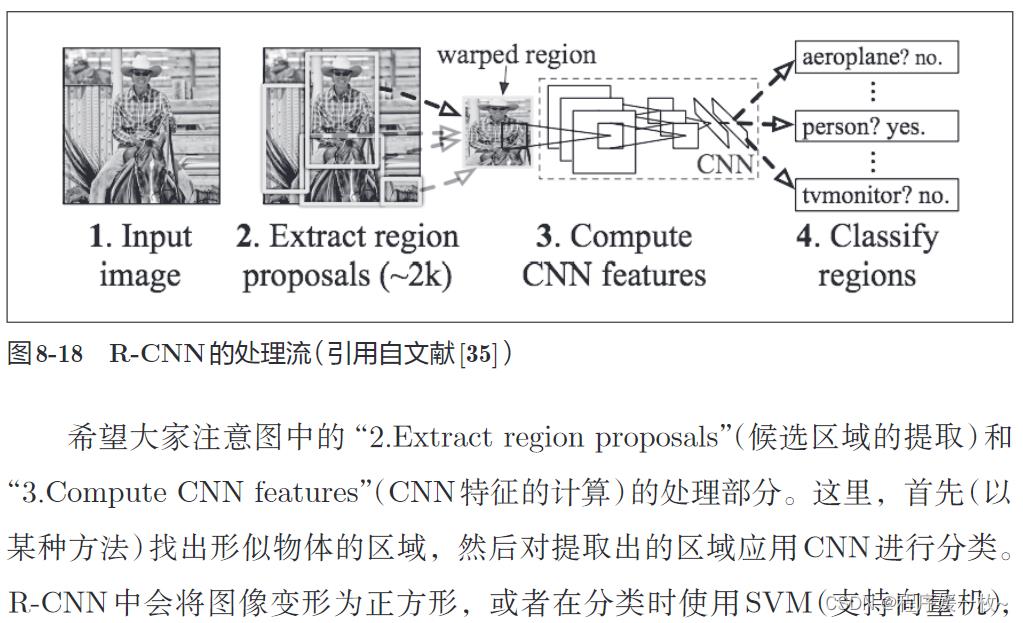
  2. Extract region proposals”（候选区域的提取）和“3. Compute CNN features”（CNN 特征的计算）。 首先（以某种方法）找出形似物体的区域，然后对提取出的区域应用 CNN 进行分类。
  2-候选区域的提取，可以用一种被称为 Selective Search 的方法，最近还提出了一种基于 CNN来进行候选区域提取的 Faster R-CNN 方法。Faster R-CNN 用一个 CNN来完成所有处理，使得高速处理成为可能。 Faster-RCNN

• 图像分割
  图像分割是指在像素水平上对图像进行分类。使用以像素为单位对各个对象分别着色的监督数据进行学习。然后，在推理时，对输入图像的所有像素进行分类。

• 图像标题的生成
  一个基于深度学习生成图像标题的代表性方法是被称为 NIC（Neural Image Caption）的模型。NIC 由深层的 CNN 和处理自然语言的 RNN（Recurrent Neural Network）构成。RNN 是呈递归式连接的网络，经常被用于自然语言、时间序列数据等连续性的数据上。
  NIC 基于 CNN 从图像中提取特征，并将这个特征传给 RNN。RNN 以CNN 提取出的特征为初始值，递归地生成文本。
  NIC 是组合了两个神经网络（CNN 和 RNN）的简单结构。基于 NIC，可以生成惊人的高精度的图像标题。我们将组合图像和自然语言等多种信息进行的处理称为多模态处理。多模态处理是近年来备受关注的一个领域。
  > RNN 的 R 表示 Recurrent（递归的）。这个递归指的是神经网络的递归的网络结构。根据这个递归结构，神经网络会受到之前生成的信息的影响（换句话说，会记忆过去的信息），这是 RNN 的特征。比如，生成“我”这个词之后，下一个要生成的词受到“我”这个词的影响，生成了“要”；然后，再受到前面生成的“我要”的影响，生成了“睡觉”这个词。对于自然语言、时间序列数据等连续性的数据，RNN 以记忆过去的信息的方式运行。

• 深度学习的未来
  图像风格变换与图像生成
  图像风格变换（Artistic Style）是使用深度学习来“绘制”带有艺术气息的画。如图输入两个图像后，会生成一个新的图像。两个输入图像中，一个称为“内容图像”，另一个称为“风格图像”
  
  图像生成是生成新的图像时不需要任何图像（虽然需要事先使用大量的图像进行学习，但在“画”新图像时不需要任何图像）。比如，基于深度学习，可以实现从零生成“卧室”的图像。下图是基 于 DCGAN（Deep Convolutional Generative Adversarial Network）方法生成的卧室图像的例子。
  生成的图像是现实中不存在的图像，DCGAN 中使用了深度学习，其技术要点是使用了 Generator（生成者）和 Discriminator（识别者）这两个神经网络。Generator 生成近似真品的图像，Discriminator 判别它是不是真图像（是Generator 生成的图像还是实际拍摄的图像）。 像这样，通过让两者以竞争的方式学习，Generator 会学习到更加精妙的图像作假技术，Discriminator 则会成长为能以更高精度辨别真假的鉴定师。两者互相切磋、共同成长，这是GAN（Generative Adversarial Network）这个技术的有趣之处。在这样的切磋中成长起来的 Generator 最终会掌握画出足以以假乱真的图像的能力（或者说有这样的可能）。
  监 督 学 习（supervised learning）& 无监督学习（unsupervised learning）

• 自动驾驶-图像分割
  
  强化学习（reinforcement learning） Deep Q-Network（通称 DQN）的方法。该方法基于被称为 Q 学习的强化学习算法。

人工智能 AlphaGo击败围棋冠军的新闻受到了广泛关注。这个AlphaGo 技术的内部也用了深度学习和强化学习。 AlphaGo 学习了3000 万个专业棋手的棋谱，并且不停地重复自己和自己的对战，积累了大量的学习经验。AlphaGo 和 DQN 都是 Google 的 Deep Mind公司进行的研究，该公司今后的研究值得密切关注。

• 对于大多数的问题，都可以期待通过加深网络来提高性能。
• 在最近的图像识别大赛 ILSVRC 中，基于深度学习的方法独占鳌头，
使用的网络也在深化。
• VGG、GoogLeNet、ResNet 等是几个著名的网络。
• 基于 GPU、分布式学习、位数精度的缩减，可以实现深度学习的高速化。
• 深度学习（神经网络）不仅可以用于物体识别，还可以用于物体检测、
图像分割。
• 深度学习的应用包括图像标题的生成、图像的生成、强化学习等。最近，
深度学习在自动驾驶上的应用也备受期待。

参考

• http://www.ituring.com.cn/book/1921