超越所有人的成就，牛顿的光芒也无法掩盖的天才数学巨人

Posted 2022-09-06 turingbooks

德国哲学家数学家 戈特弗里德·威廉·莱布尼茨（1646-1716）

艾萨克 • 牛顿堪称所有时代最伟大的数学家之一。他的成就无数，而其中超越所有人的成就是开创了微积分。

他与同时代人莱布尼茨一起分享这一荣誉。事实上, 是莱布尼茨给出了这门学科的明确记法甚至是名字。

然而，因牛顿率先开创了微积分而把他置于数学巨匠名单之首的学者们却常常忽视莱布尼茨，尽管他也开创了微积分。在某种程度上，莱布尼茨似乎被遗忘了。这不仅不公平也很不幸，因为在很多方面，莱布尼茨的故事和牛顿的一样, 也非常引人注目。

01

十年学法

1646年戈特弗里德 • 威廉 • 莱布尼茨（Gottfried Wilhelm Leibniz）出生于莱比锡。还是个孩子的时候，他就显示出广泛的阅读兴趣，而且他似乎拥有以惊人的速度学习任何东西的能力。莱布尼茨也许是一位令人难忘的学者，他在十五岁那年进入大学。三年后他得到了学士和硕士学位, 不久之后得到了阿尔特多夫大学的法学博士学位，大有“一览众山小”的气势。

与此同时在剑桥大学，牛顿正在夜以继日地研究他那非凡的流数。而莱布尼茨尽管完成了很多学科的学习，但是此时他对数学还是知之甚少。

几十年后他回忆说：“1672年, 当我到达巴黎时，我自学了几何，我的确对此学科知道的很少，对这门学科，我没有耐性去看那一长串的证明。”甚至欧几里得对他来说都是个很神秘的人物，当时他碰巧看到了笛卡儿的《几何》，他发现它太难了。没有人能够想到仅在几年内，莱布尼茨的诸多发现会使他跻身数学巨人之列。

法律占据了莱布尼茨接下来十年的大好时光。他受雇为美因茨选帝侯的顾问，并以这一身份承担外交使命，于1672年3月前往巴黎。

事实证明, 这一工作是他人生中重要的经历。这位年轻的外交官醉心于他在那里感觉到的美术、文学和科学的活力。他爱上了巴黎以及这一时期巴黎所展示出的一切，爱上了“太阳王”的都城。

02

惠更斯的数学评估

与伟大数学巨人的觉醒

在法国首都居住的众多知识分子当中，对莱布尼茨影响最大的是荷兰科学家克里斯蒂安 • 惠更斯（Christiaan Huygens, 1629—1695）。在这一重要时期，惠更斯充当着良师益友的角色，他想要评估一下这位年轻朋友的数学敏感性，于是向莱布尼茨发出挑战，要求他求解下面的无穷级数的和

（第n个分数的分母是前n个正整数之和。）

　　

莱布尼茨仅凭着自身的聪明而不是过去已有的训练在实验几次后把这个级数重写成

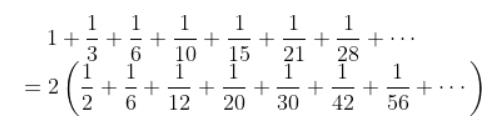
然后，把括号中的每一个分数表示成两个分数，他把上式右边变成

方括号中第一项之后的所有项都消掉了。用这样的方法，他正确地计算得到

　　

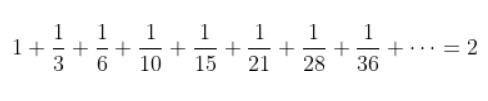
这位数学新手已通过了惠更斯的测试。关于这个问题在莱布尼茨的生涯中所起的作用，历史学家约瑟夫 • 霍夫曼发表了评论，他说：“那个例子如果再稍微难一点（莱布尼茨解不出来），那毫无疑问将浇灭他对数学的热情。”若是如此，成功就不会光顾他。

　　

莱布尼茨不仅解决了一个问题。因被无穷级数所吸引，他思考了很多其他例子。后来他说，对这样一些和的研究，显然是他发现微积分的关键。这已成为莱布尼茨数学的标志，他就是要寻求一个基本原则，该原则能够把诸多类似问题组成的一大类问题统一起来。

在很大程度上，他的天才赋予了他这样的能力，能够发现连接似乎不相关的特殊例子的一般法则。实现这样的分析需要敏锐的智慧，而莱布尼茨当然拥有这样的智慧。

　　

他的工作的第二个特点是重视好的数学记法。他推行一套收集了很多符号和法则的“人类思维字母”，如果能够照其行事，它也许会确保人们在数学乃至日常生活中做出正确的推理。

尽管这一宏伟计划从来没有变成现实，但被视为现代符号逻辑的前身。尽管莱布尼茨没有成功地符号化人类的思维，但是他引入的微积分记法却一直沿用至今。

　　

在巴黎，他的智力旅行不断加速。他惯于博览群书，而且他的外交工作也对此带来影响，但是他还是很快进入数学的前沿阵地。

到了1673年春天，他正式开始自己的研究。莱布尼茨回忆说：“此时我已经为自己独立前进做好了准备，因为我读（数学）几乎如同他人读浪漫故事一样。”

戈特弗里德 • 威廉 • 莱布尼茨
（拉法耶特学院图书馆惠允）

现在，有些发现被认为是出于好奇心。例如，他解决了一个富有挑战性的问题，找到了和为完全平方且其平方和为完全平方的平方的三个数（这类神秘问题在他那个时代很流行）。莱布尼茨发现的数是64、152和409，它们的和是

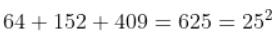
这是一个完全平方，而它们的平方和是

这是一个平方的平方。他是如何发现这些数的并不重要，我们要强调的是：他不是通过猜测得到的。[6]莱布尼茨还发现了下面这个古怪的公式

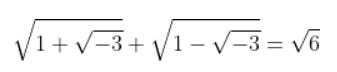
这个公式不仅令世界上某些大数学家感到困惑（某种意义上也包括莱布尼茨自己），而且还帮助普及了虚数。

03

我们的微积分是莱布尼茨的微积分

这一切只是莱布尼茨数学生涯伟大篇章的序曲。随着在他巴黎寓所的工作的进展，他不断深入研究，到了1675年的秋天, 他已经拥有这个“新方法”，也就是我们现在所说的微积分。这段时光对他来说是愉快的，而对数学来说是非常重要的。

当现代观光客在巴黎的街道上散步时，他们总是会想到诞生于这座伟大城市的美术、音乐和文学作品，维克托 • 雨果或图卢兹-洛特雷克这样的人物好像重生了。但是，很少有人会意识到在三个多世纪前，同样的林荫道也见证了微积分的诞生。如果巴黎造就了伟大的艺术，它同样也造就伟大大的数学。很少有人意识到这一点，这也表明了莱布尼茨被严重遗忘了。

他的外交使命从1672年开始持续到1676年秋天，这年秋天他回到他的祖国德国。正是在德国，他于1684年发表了微分学的第一篇论文。两年后，第二篇论文介绍了这门学科的另一个分支——积分学。

事实上，当时的微积分思想还有很多逻辑不足。因此，它只能反映早期不成熟的积分思想。当后来的数学家充分掌握了这一思想后，他们遇到了令人难以理解的理论障碍，而这些障碍直到19世纪的近代才得以解决。

但是，戈特弗里德 • 威廉 • 莱布尼茨有资格分享属于他的荣耀。造化弄人，莱布尼茨生活在牛顿的时代，如果说牛顿这颗明亮的星星使莱布尼茨在公众记忆中的形象黯然失色, 那么也可以说，牛顿这颗明星将使所有星星都失色。

但是，数学界还是给莱布尼茨以充分的肯定。与牛顿一样，他发现了微分和积分的伟大思想，并且认识到微积分基本定理是二者之间的桥梁；与牛顿不同的是，他与世界分享了这些成果。因此，莱布尼茨启发了其他人，特别是伯努利兄弟，通过他们个人的研究和相互交流，他们构思了今天我们所知道的这门学科。就某些现实意义来说，我们的微积分是莱布尼茨的微积分。

该说的都说了，该做的都做了，在数学历史上这样一个重要时刻，重要的事实是这两位伟大的天才——牛顿和他的同辈莱布尼茨——同时发挥着作用，而不是一个人独领风骚。

深受读者喜爱的十年经典，千呼万唤的好书再版重出

看完顿感舒爽，让数学课堂上的知识变得更好懂、更通透

无需动用纸笔，纵览数学世界不可不谈的伟大定理、难题和争论

好奇心大满足，纵览数学的核心知识和历史八卦