非参数bootstrap方法, 小数据集统计的大能手

Posted 2021-04-29 计量经济圈

凡是搞计量经济的，都关注这个号了

邮箱：[e-mail]

所有计量经济圈方法论丛的code程序, 宏微观数据库和各种软件都放在社群里.欢迎到计量经济圈社群交流访问.感谢@aha 群友分享.

下面这两篇文章都有引荐“bootstrap”方法：

在统计学中，自助法（Bootstrap Method，Bootstrapping或自助抽样法）是一种从给定训练集中有放回的均匀抽样，也就是说，每当选中一个样本，它等可能地被再次选中并被再次添加到训练集中。自助法由Bradley Efron于1979年在《Annals of Statistics》上发表。当样本来自总体，能以正态分布来描述，其抽样分布(Sampling Distribution)为正态分布(The Normal Distribution)；但当样本来自的总体无法以正态分布来描述，则以渐进分析法、自助法等来分析。采用随机可置换抽样(random sampling with replacement)。对于小数据集，自助法效果很好。

最常用的一种Bootstrap自助法，假设给定的数据集包含d个样本。该数据集有放回地抽样m次，产生m个样本的训练集。这样原数据样本中的某些样本很可能在该样本集中出现多次。没有进入该训练集的样本最终形成检验集（测试集）。 显然每个样本被选中的概率是1/m，因此未被选中的概率就是(1-1/m)，这样一个样本在训练集中没出现的概率就是m次都未被选中的概率，即(1-1/m)^m。当m趋于无穷大时，这一概率就将趋近于e^-1=0.368，所以留在训练集中的样本大概就占原来数据集的63.2%。

例如：人工样本为1，2，3；只有三个样本，则可以从随机变量X，分布为P(X=k)=1/3, k=1,2,3; 这样的经验分布中用计算机根据上述分布自动产生样本，如产生5个样本：1 2 3 2 1；也可以是：3 3 2 1 1。

自助法在数据集较小、难以有效划分训练集和测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。因此，在初始数据量足够时，留出法和交叉验证法更常用一些。

下面，咱们通过一列slides来看看bootstrap方法。如果不懂这些具体运算，对这种方法有大致的印象也对今后的研究工作有很大的帮助。

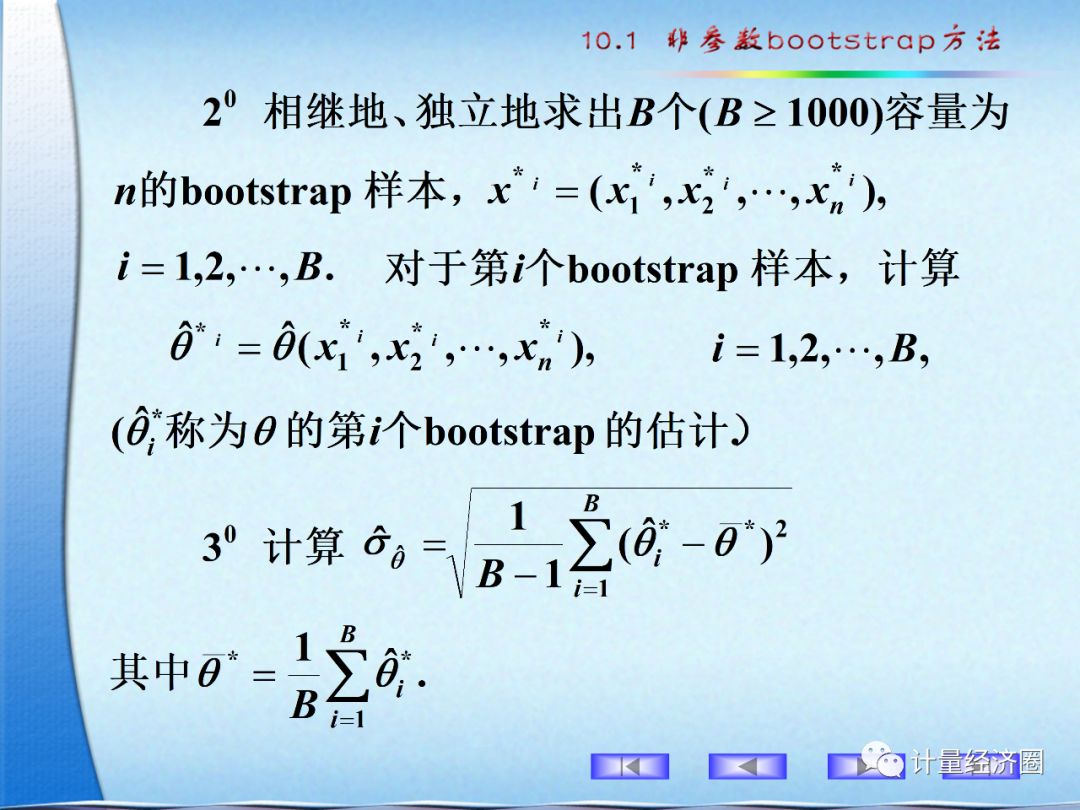
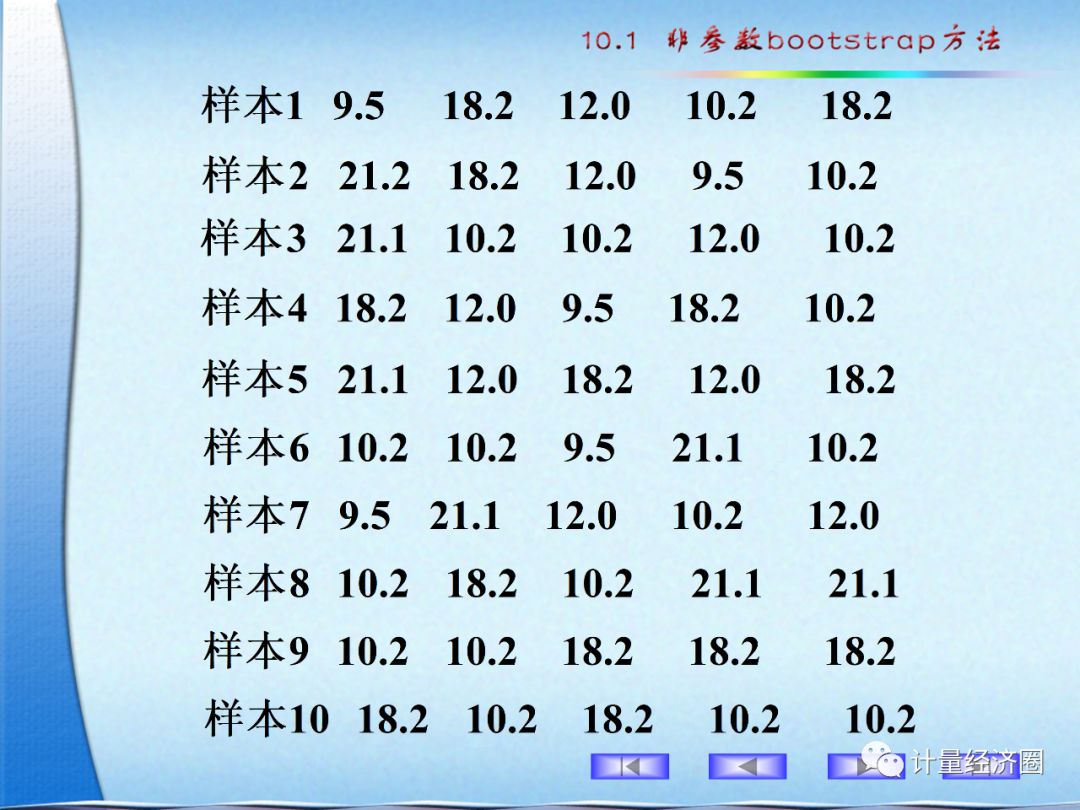
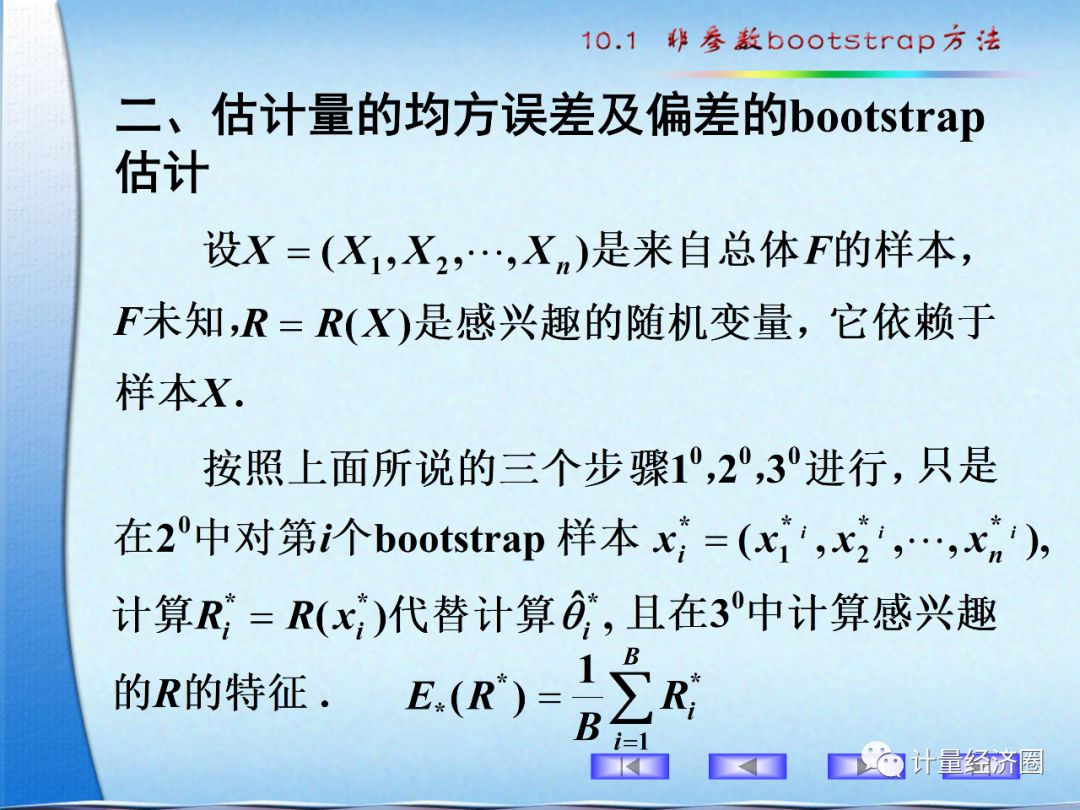
可以到计量经济圈社群交流访问。

推荐阅读：

1.工企

2.

3.

4.

5.

所有计量经济圈方法论丛的code程序, 社科数据库和各种软件都放在社群里.欢迎到计量经济圈社群交流访问.

可以到计量经济圈社群进一步访问交流各种学术问题，这年头，我们不能强调一个人的英雄主义，需要多多汲取他人的经验教训来让自己少走弯路。

计量经济圈当前有几个阵地，他们分别是如下4个matrix：

①小鹅社群：数据软件书籍等所有资料(最多且更新频繁)，

②微信群：服务于计量经济圈社群群友(最活跃)，

③研究小组：因果推断, 空间计量, 面板数据(最专业)，

④QQ群：2000人大群服务于社群群友(最大)。

只有进去之后才能够看见这个群公告