虾说区块链-83-blockchain笔记二

Posted 2021-04-29 磨链mochain社区

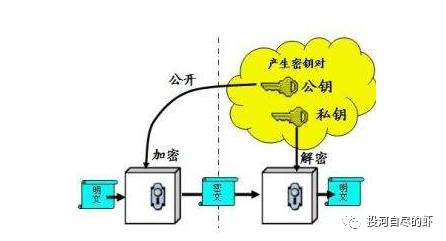
1976年后，密码学有一个颠覆性的改进，非对称加密的概念被提出来，简单来说：A和B之间信息交互，A生成两把密钥：公钥和私钥，然后公钥公开给B，B通过A提供的公钥加密，把加密后数据给A，A通过私钥解密或许数据。

 

针对这种加解密概念，RSA公钥加密算法被提出，RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。1987年7月首次在美国公布，当时他们三人都在麻省理工学院工作实习。RSA就是他们三人姓氏开头字母拼在一起组成的。RSA是目前最有影响力和最常用的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。（百度百科）

   

RSA算法基于一个十分简单的数论事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

下面对RSA算法简单介绍下：

数学中的质数定义为：一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数。100以内的质数：2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97。RSA算法中提出两个正整数，除了1之外没有其他公因子，那么定义为互质关系。自然而然质数和质数之间肯定是互质关系。

比如：11-13、13-17、17-23.。。。

推导互质关系可以得出下列结论：

1.A是质数，B不是A的倍数，那么A\B互质关系。（如：29-60）

2.任意两个正整数，较大的一个是质数，那么就是互质关系。（如：97-60）

3.A是质数，A和A-1是互质关系。（如：29-28）

4.A是质数，A和A-2是互质关系。（如：29-27）

5.1和所有正整数都是互质关系。

针对互质问题，那么在小于等于n的正整数中，有多少个和n构成互质关系，这里引出欧拉定理，欧拉定理是RSA算法的核心六楼，这里只是简单说下欧拉定义关于证明请详见（https://baike.baidu.com/item/%E6%AC%A7%E6%8B%89%E5%AE%9A%E7%90%86/891345?fr=aladdin）欧拉定理表明，若n,a为正整数，且n,a互质则：

 

a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

再加一个模反元素的概念，如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。这个b叫a的模反元素。举例：3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {...,-18,-7,4,15,26,...}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。直接看一些数学类解释比较累，数学不好的同学应该会被绕的不行，笔者参考：http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html

 

欧拉定理可以用来证明模反元素必然存在。

接下来说说RSA算法，RSA算法是一种非对称密码算法，所谓非对称，就是指该算法需要一对密钥，使用其中一个加密，则需要用另一个才能解密。RSA的算法涉及三个参数，n、e1、e2。其中，n是两个大质数p、q的积，n的二进制表示时所占用的位数，就是所谓的密钥长度。e1和e2是一对相关的值，e1可以任意取，但要求e1与(p-1)*(q-1)互质；再选择e2，要求(e2*e1)mod((p-1)*(q-1))=1。（n，e1),(n，e2)就是密钥对。其中(n，e1)为公钥，(n，e2)为私钥。RSA加解密的算法完全相同，设A为明文，B为密文，则：A=B^e2 mod n；B=A^e1 mod n；（公钥加密体制中，一般用公钥加密，私钥解密）e1和e2可以互换使用，即：

A=B^e1 mod n；B=A^e2 mod n;

看算法解释还是很绕，通过一个交易过程来说明：

A和B两个进行交易，A首先选择一对质数，因为是举例所以选择数比较小，实际中根据质数位数，安全性有相应的提升，一般小位的RSA算法已可通过暴力破解来解密，所以实际应用中位数选择也是很重要的，根据位数来设置安全权限等级高低。

1.A选择一对质数，x、y，然后将x*y=z，把z写成二进制表达（二进制位数决定安全性高低）。

2.根据欧拉函数计算，p=（x-1）*（y-1）

3.随机选择一个整数q。1<q<p，p和q互质

4.结合模反元素计算d的值，ed ≡ 1 (mod φ(n))--ed - 1 = kφ(n)--ex + φ(n)y = 1（推导计算），实际就理解q*x+p*y=1。这里具体计算就不写了有兴趣去查下扩展欧几里得算法（绕的我不信）

5.接下来稍微脱离下数学知识，刚刚计算的那些值：z、p、q、d，封装下（z、q）公钥，（z、d）私钥。

上面就是整个公钥和私钥的生成。任何算法都要考虑他的逆推时候会可行。

私钥中的d是关键的数字，那么已知（z、q）推导d，由于q是随机选择的，z又和私钥相关，可知z能否逆推变得很重要。分析下z：

z因数分解（把一个整数分解成两个或更多的除1外的整数相乘的过程），我们假设一个16,2-8、2-2-4、4-4等，那么你选择一个4位数或者8位数，测试下能计算出多少种可能，再结合现实场景一个16位以上乘以16位以上，你再计算他的因数分解。这个难度值还是不否认还是比较高的吧。

结合加解密过程再说明：

1.首先是加密，选择一个数字加密，数字为m 那么加密：m的q次方=加密后值（mod z）。

2.解密，加密后的值的d次方=m（mod z），解密后m和之前m一致。

最后总结说下，这个过程数学证明和推导很复杂但是概念很清楚：私钥加密后数据公钥可以解密，公钥加密后数据私钥可以解密，基础就是两个大质数的乘积难以逆向求解，所有我们就认为公钥私钥是对等但不一致。也就是说为的非对称密钥。

 

看下安全级别和密钥长度的关系表：

 

本文由币乎(bihu.com)优质内容计划支持。

笔者微信：