数学大师 | 最短路径问题——穿越虫洞

Posted 2021-04-28 数学大师

两点之间，直线最短 似乎是我们的共识，

然而在多维的宇宙中，虫洞却是一种未被印证的可能。

1930年爱因斯坦及罗森提出假设，

透过虫洞可以做瞬时的空间转移或者做时间旅行。

唐朝诗人李颀在《古从军行》中说“白日登山望烽火，黄昏饮马傍交河。”诗中隐含一个有趣的数学问题。

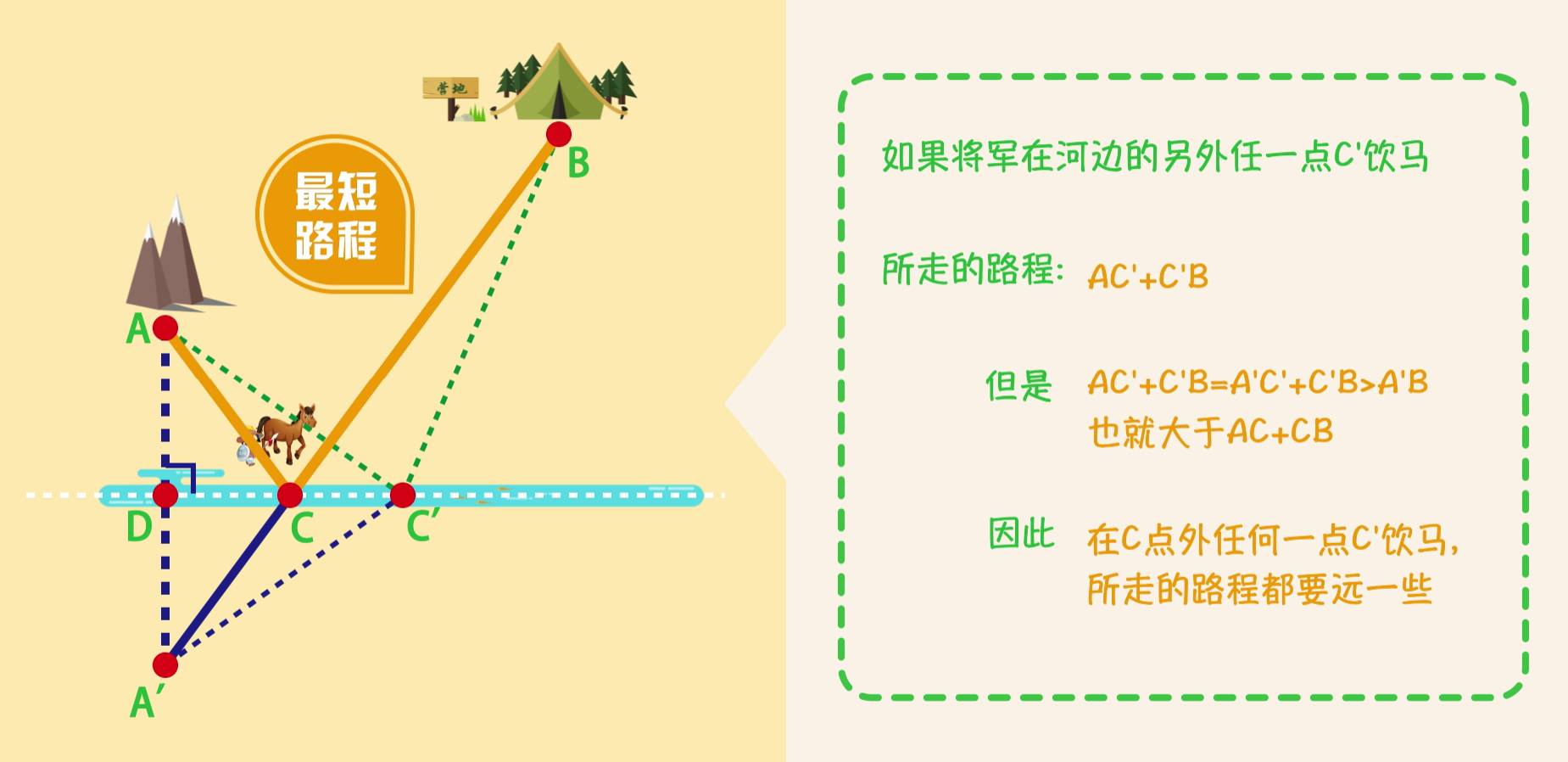
【例1】诗中军人在观望烽火之后从山脚下的A点出发，走到河边饮马后再到B点宿营，请问怎样走才能使总的路程最短？

解决办法就是：

从A出发向河岸引垂线，垂足为D，

在AD的延长线上，取A关于河岸的对称点A'，

连结A'B，与河岸线相交于C，

则C点就是饮马的地方，

将军只要从A出发，沿直线走到C，

饮马之后，再由C沿直线走到B，

所走的路程就是最短的。

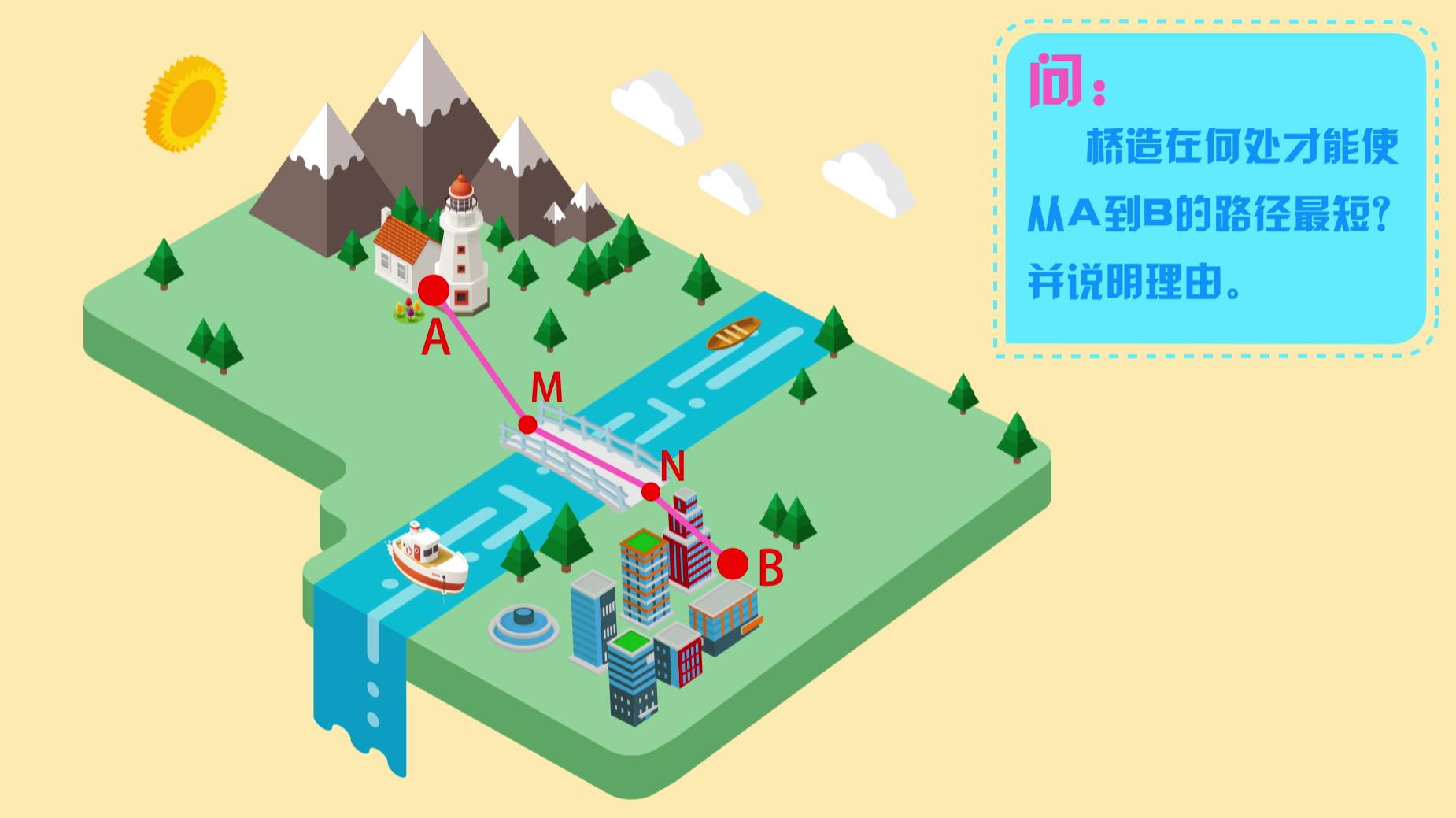
关于最短路径，还有一个有名的造桥选址问题：

【例2】A、B两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处才能使从A到B的路径最短？并说明理由（假定河的两岸是平行的直线，桥要与河垂直。）

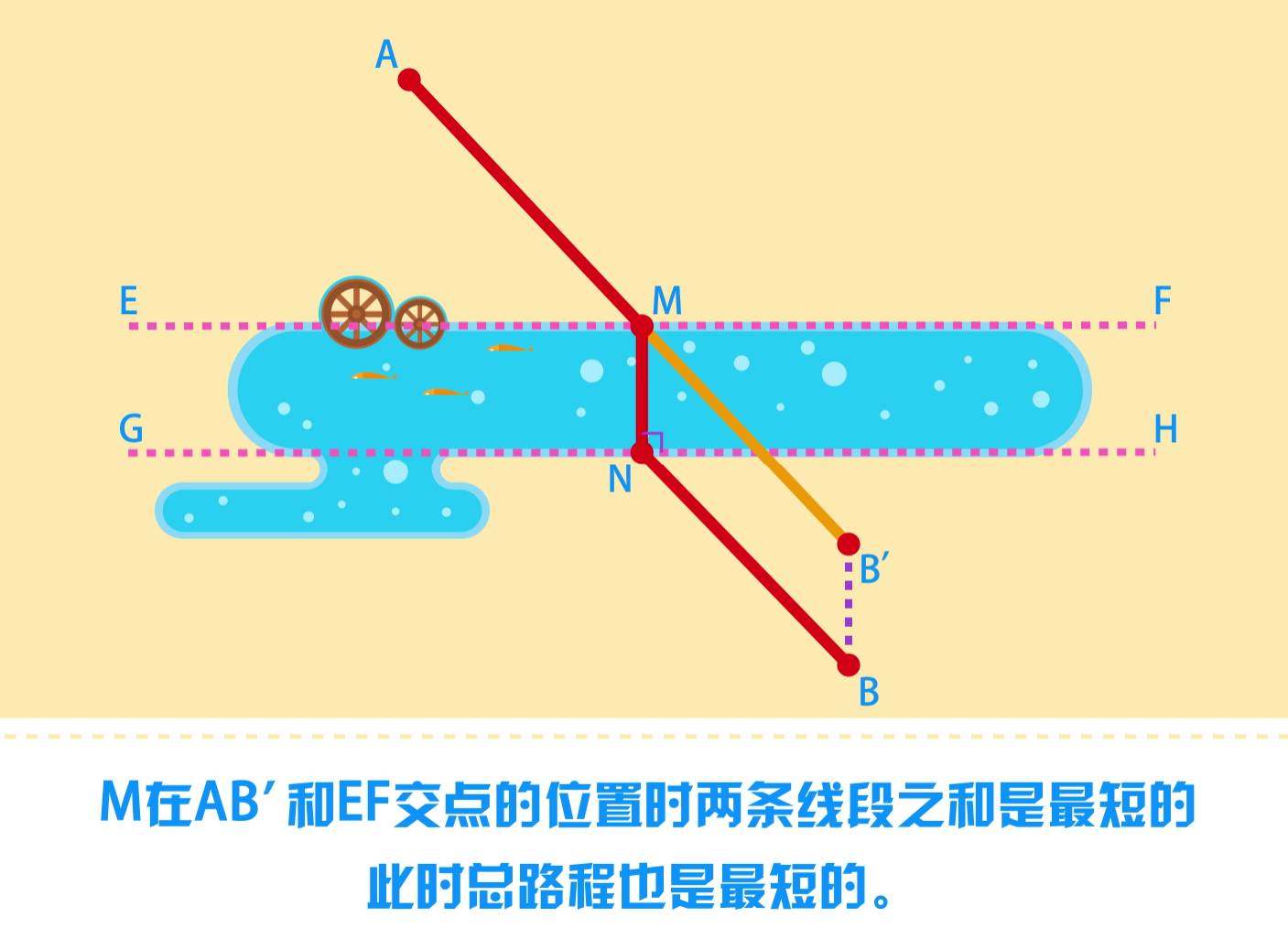
将BN平移到B′M，此时BN M B′是平行四边形。

并且我们注意到，

因为河宽不变，无论mn在何处，

B′的位置是不变的，

于是问题就变为了AM 与B′M何时取到最小值。

由于两点之间线段最短，

所以显然M在AB和EF交点的位置时两条线段之和是最短的，

此时总路程也是最短的。

高中数学即将上线，敬请期待！

后台回复“0”免费观看所有知识点视频

↓↓↓点击“阅读原文”，获得所有数学精品课程！