安全数据分析:数据点—地图—线性回归
Posted 计算机与网络安全
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了安全数据分析:数据点—地图—线性回归相关的知识,希望对你有一定的参考价值。
一次性进群,长期免费索取教程,没有付费教程。
ID:Computer-network
知道了这些地理数据代表ZeroAccess的宿主位置,我们就可以通过将一些看起来并不重要的数据跟基本数据放在一起研究,并通过这种方式发掘其中的利益(以及陷阱)。通过关联、合并相关的数据,往往能够获得比原始数据更多的信息。因此,当回到实际工作中时,应当记住不要仅仅关注收集到的基本数据,而是要试着发掘这些数据与从周围环境中收集到的其他数据之间的关系。例如,可以通过以下问题将多个数据源关联起来:
网站的受害者和他们的人力资源数据(教育背景、收入等)之间是否有关?
(NetFlow)网络数据的模式和在主机上运行的软件、服务之间是否有关?
员工的上网习惯和他们的生产率或绩效评估得分之间是否有关?
下面将从一个单独的数据点(感染过ZeroAccess的系统的位置数据)入手,一步步探索数据的内部关系。将把位置数据和其他地理上的观察结果关联到一起,并通过名为线性回归(linear regression)的统计学手段测试各个数据点之间的关系,找到其中的关键关系(甚至是伪关系)。本文示例使用R语言。
一、简化地图
很容易认为可视化空间数据(地图)是特殊、复杂并且要花费很多精力的。但是只要使用适合的工具(目前已有很多可用工具),处理空间数据实际上是一件比较简单并且有趣的工作。为了挖掘地图的奥秘,我们首先要做的是载入从赛门铁克得到的经纬度数据点,并以它们作为x和y坐标来画出一幅散点图(见图1)。

图1
图2很像一幅没有画出国界标出具体功能的世界地图。这样的地图使用数据也可以画得出来,因为超过了800000组坐标,画出的每一个点都覆盖了超过一座大型城市的大小。通过将alpha值(即颜色的透明度)设置为1/40可以让这些点看起来不会过于突兀。如果设置为1/40,那就需要重叠40个点才能形成一个完全不透明的点。而如果重叠20个点,那么它的透明度就是50%。
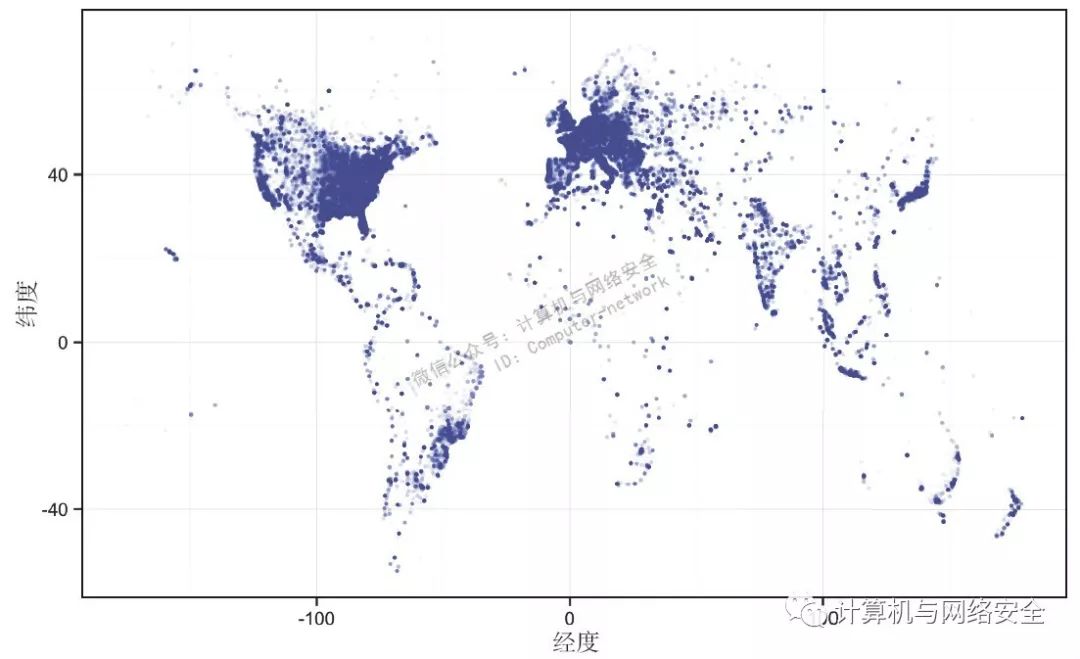
图2 使用经纬度绘制的散点图
从这个散点图中,可以看到西海岸和整个东部以及大部分的欧洲都被覆盖了,巴西的局部以及印度的大致轮廓也同样被覆盖了。然而有趣的是,中国几乎完全没受到影响,而日本却清晰可见。
这张图与众不同之处在于需要将三维的球体世界投影到二维的画布之上。在这一过程中,地图的一些特征将被扭曲,形状会被扭曲、陆地部分会被缩小或者放大、距离也会变得偏斜。但是在领域内,只是试图展示地理区域上的某些特性或者区别。因此在选择地图投影法的时候可以充分考虑美感以及您的个人偏好,而不需要特意表现出某一种地理信息。图3展示了一些不同的地图投影法。
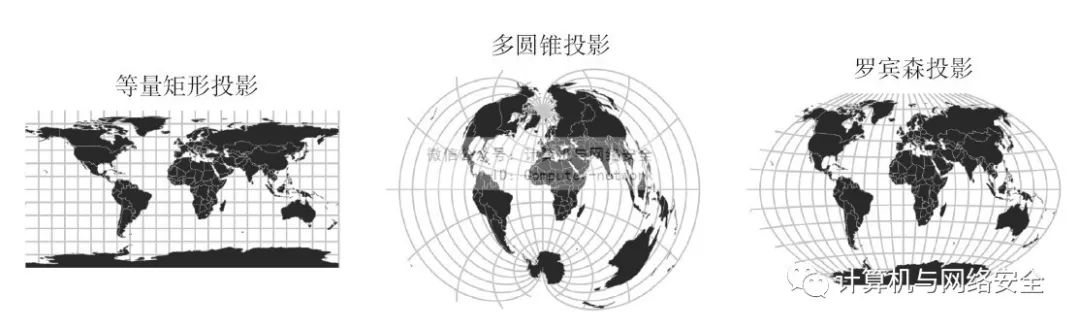
图3 地图投影法
现在再回顾一下图2,除非高中地理课上你没有打过瞌睡,否则您很难知道那些点都指的是哪些地方。现在您来重新创建这幅图,首先根据陆地板块画出地图,之后再在上面添加数据点。幸运的是,只要安装了R语言的一些程序包,您就拥有了大部分的基础地图数据。ggplot2程序包中定义了一个map_data()函数,它封装了map数据包,返回一个兼容ggplot2程序包的数据帧。
使用字符串“world”来调用map_data()函数时,程序会将2.5万行的地图数据加载进一个数据帧。这意味着可以使用str()、head()和summary()命令在数据中任意探索。另外,还可以通过数据集中的经纬度构成的路径,来画出国家的边界。其中路径存放在标记为group的列中(在该数据中,组指代国家),而数据帧则必须按顺序排列(这是一个重要的细节,会在之后看到)。为了创建最终的地图(参见图4),需要调用coord_map()来创建地图投影(在这个例子中使用墨卡托投影法),并使用theme_bw()来设置简单的黑、白主题颜色。当画出国界后,再像之前创建散点图时所做的那样,从ZeroAccess数据中向地图添加点(参见图5)。

图4
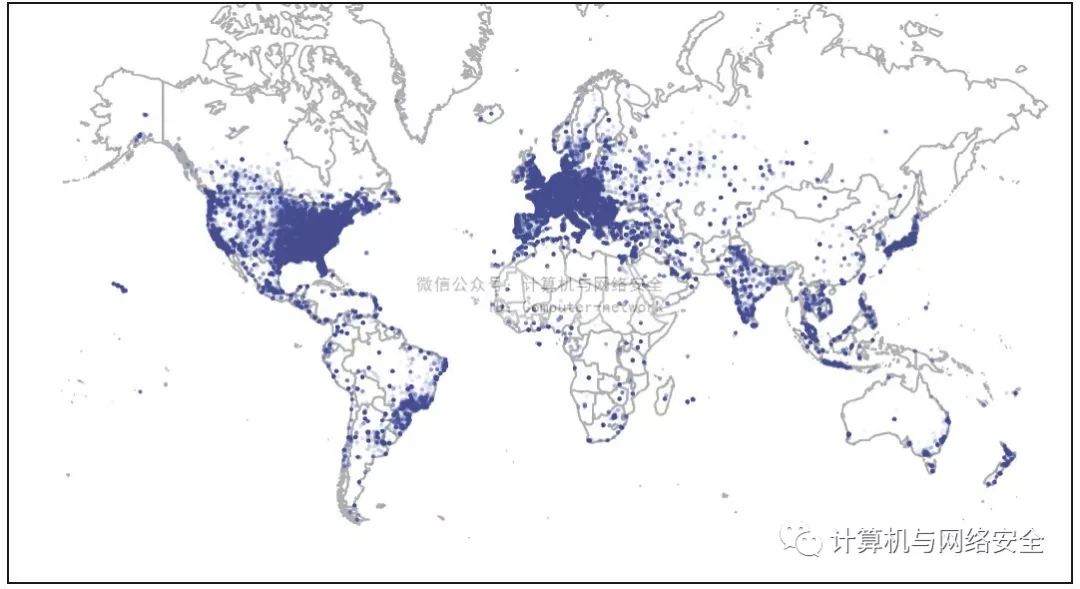
图5 世界范围内的ZeroAccess木马感染情况
现在得到了一幅真正的地图,但是能从中得到什么信息?其实并不是很多。这幅地图仅仅告诉了您ZeroAccess在世界范围内都有感染案例,但是您已经知道这一点。因此您要更进一步,研究如何才能使用地图来更好地可视化这些数据。
1、每个国家的ZeroAccess木马感染量是多少
仅凭图5很难判断哪个国家的感染量最高。没人能够从这样的地图中看出各个国家的感染比例,能看到的只是和欧洲已经被覆盖了。现在尝试一种不同类型的地图。您先要获知每个国家的感染量是多少,然后将结果使用一张分级统计图(choropleth)进行可视化。在分级统计图中,国家将会被填充颜色,并通过这种方式与数据关联起来。对于第一幅分级统计图,需要知道经纬度坐标是在哪个国家之内,然后再使用连续的颜色刻度来代表相应的数量(参见图6)。使用Ryan Weald的函数并调用latlong2map()函数将经纬度坐标转换成国家。这个函数接受一个经纬度的数据帧以及一个地图名称作为参数。

图6
该函数返回一个名称向量(该例中是国家名),并且可以使用table()命令获知一个国家在该向量中出现的次数。在图7中,将使用merge()把国家出现次数与地图数据合并到一起,并将其重新排序。通过这种直接合并,可以将颜色与数据中的一个特征(特别是一个国家的感染量)关联起来。将使用ggplot2中的scale_fill_gradient2()函数来得到与感染量相关联的色阶。结果参见图8。
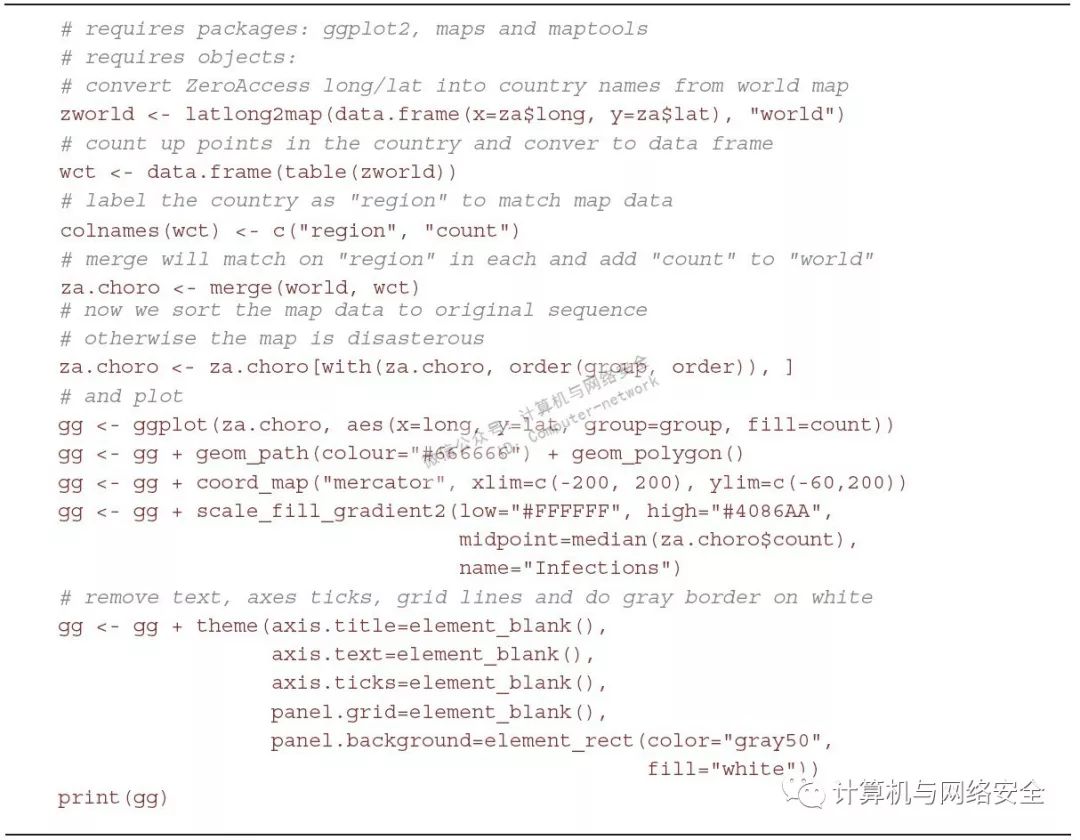
图7
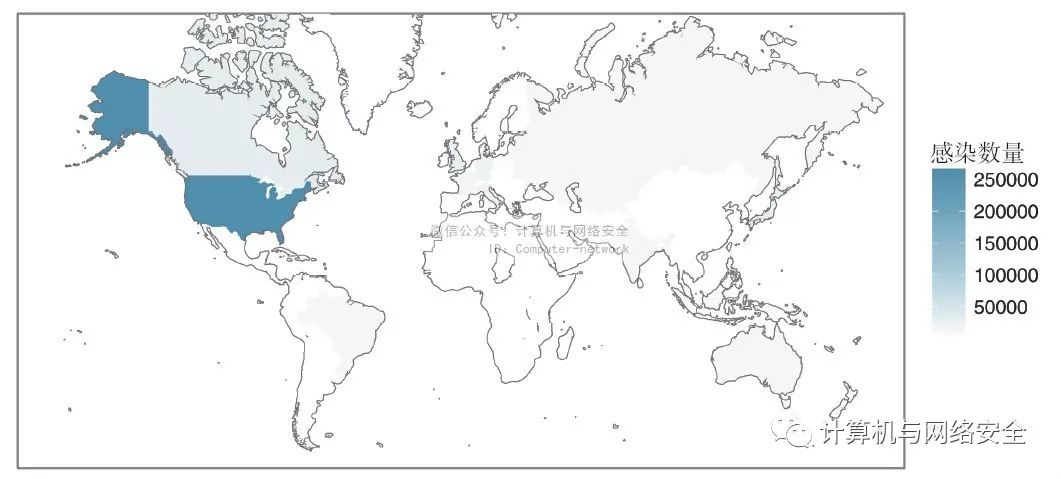
图8 感染ZeroAccess木马的分级统计图
得到了一幅很好看的(有些人可能会说“很醒目”)的地图。看起来已经将ZeroAccess的感染范围控制在自己国境内了,这个信息是从图5中得不到的。然而,要通过颜色密度来获知具体的感染数字仍然是个难题,从这幅地图中仅能够得知比别的国家有更高的感染量。而要想知道高多少,则需要查看wct变量,然后计算的感染比例(参见图9)。
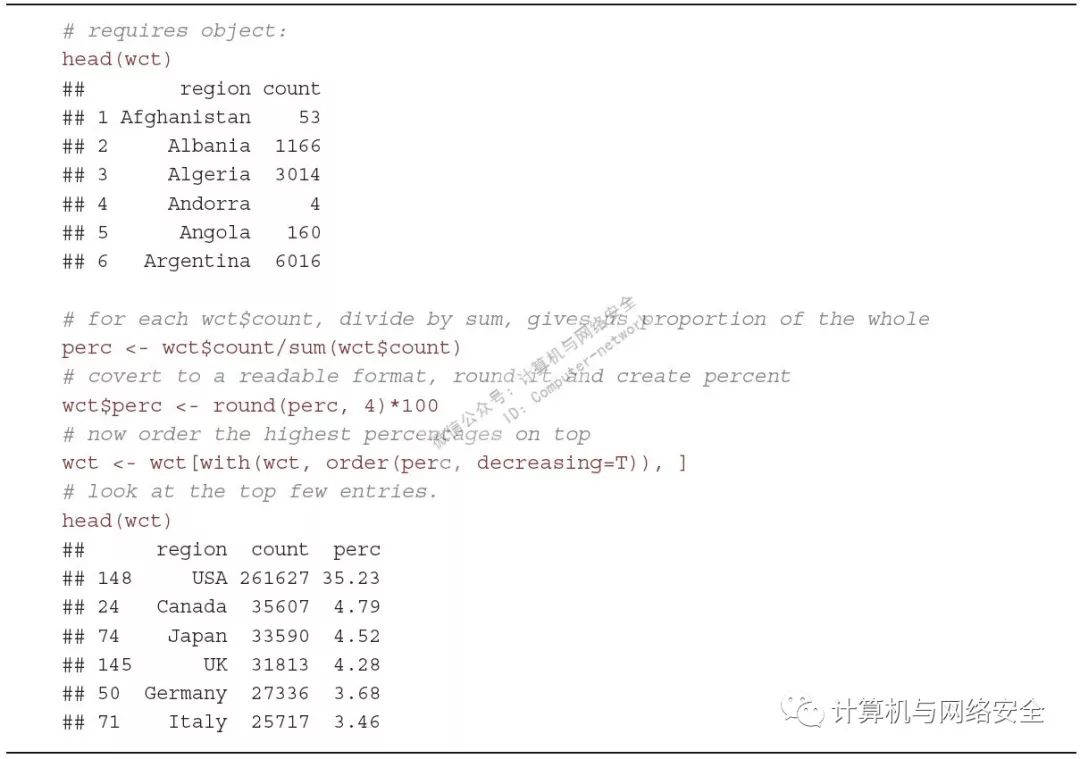
图9
可以通过这个表格回答“ZeroAccess在地域上是如何分布的?”这个问题。这幅地图实际上突出了与世界其他地区在感染量上的差距,但要记住这些只是总数,而没有考虑人口等其他因素。因此目前来看,35%只代表了ZeroAccess数据中的一个比例,而在没有进一步分析之前不应该做更多推测。
2、改变数据范围
不要忘记目标是要找到一种能够让ZeroAccess的感染情况与其他数据相关的方法。为了达到这个目的,可以将数据集简化至只剩一个国家。这么做不仅是因为在某些系统中处理800000个数据点会很慢,还因为您更了解的地理,并且更容易获取相关的数据,因此专注于将会使你的目标更加容易实现。
然而,当您像这样改变数据范围的时候,需要考虑清楚,这么做可能会改变您需要回答的问题。您不能再像以前那样将结论推广至一般,因为您不能轻易地把从的感染情况中得到的结论直接套用到别的国家或者别的文化当中。换一种说法,您不知道影响感染量的一些因素是不是同样也是影响其他地方感染量的因素。这已经超出了您所处理的数据的范围,因此在分析和展示结果的时候一定要避免做出过多的假设。
如果试图绘制出地图并将点全部投影到上面,那么ggplot中的自动比例缩放特性将会让结果看起来很滑稽。它将会显示数据集中的所有点,但只画出的地图。因此您需要减小数据量,将不在范围内的数据移除。这里可以再次使用latlong2map()函数,而这次在将点映射到地图上时要将“state”作为第二个参数传入。从R语言的角度来看,这意味着任何不能映射到的一个州的数据都将返回NA,并且从数据集中过滤掉。
当这些处理完成后,可以画出一幅很不错的地图来表现的ZeroAccess感染情况(参见图10)。注意在这幅以及上几幅图中,您一直在删除地图上多余的图表垃圾(chartjunk,Edward Tufte创造的一个术语)。为此您可以在最后使用theme()函数,并通过将图形特征赋给element_blank()来删除它们,参见图11。
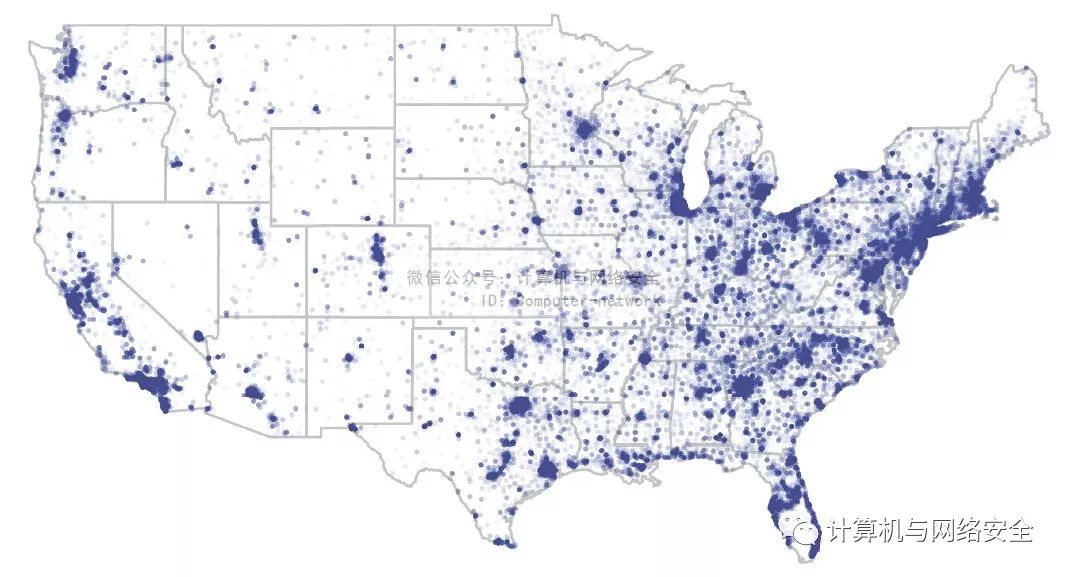
图10 美国的ZeroAccess木马感染情况
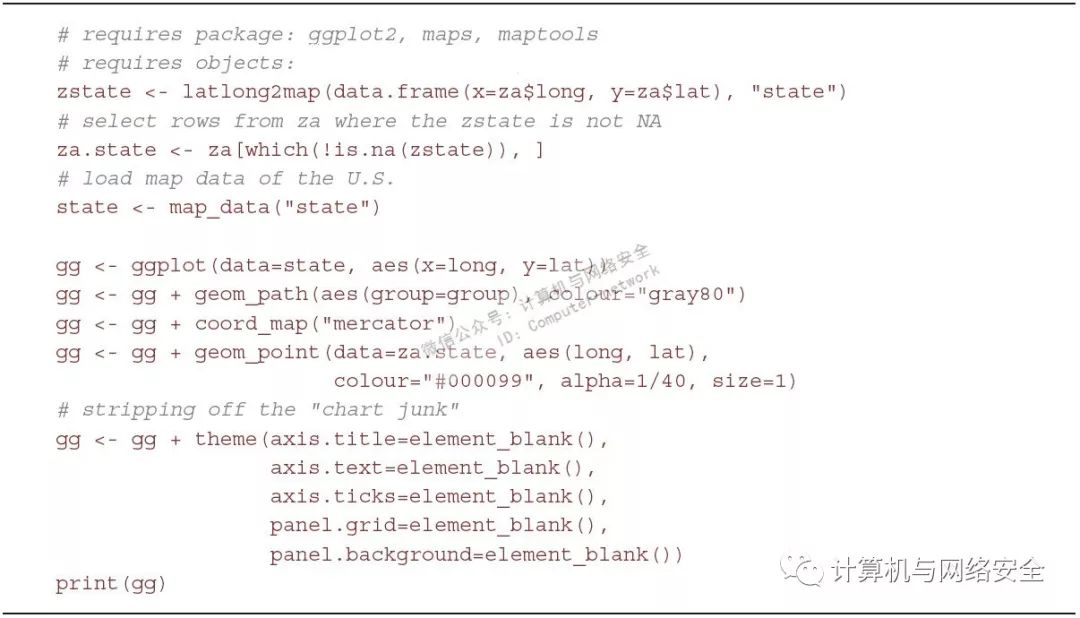
图11
来看看图10,它是不是有点……奇怪?这就是您要小心的地方,因为在操作空间数据之后我们可以告诉您“它看起来像是在反映人口密度”而“不是感染量”。因此,在回顾图10之后,您可能会问一个有点不一样的问题:“ZeroAccess感染是不是仅仅反映了当地人口数量的多少?”这里您可以停下来应用一种叫做回归分析的统计学方法,而现在您要坚持一下并再创建一幅分级统计图。这一次您要将数据打散,根据的州来计数。
3、Potwin效应
当深入挖掘而不仅限于国家时,必须考虑到以堪萨斯的一个只有449人的小镇命名的“Potwin效应”。这个人口数很重要,因为如果检查数据,将发现在Potwin镇有12643个ZeroAccess感染报告。我们首次偶然发现这种“反常”是在另一份(也是更微妙的)分析中,我们花费了数日尝试去理解为什么Potwin镇如此奇怪。而当我们有了一些关于Potwin的疯狂想法并设法证明该数据的合理性后,我们意识到这些并不是有效的数据条目。最终我们想起有若干数据点被奇怪地四舍五入成整数并且它们都是38,–97。
在这张地图上,您要再次使用颜色来表示数量。而这次不仅要使用单一的色度(一个关于颜色的花俏词汇),还会使用“分歧配色方案”(diverging color scheme两种反色),并把这个范围的中点赋值给每个州的平均数(参见图12)。这将允许您用一个色度展示高于感染数均值的州,用另一个色度展示低于均值的州。另外要提示一下,还要也把投影从墨卡托投影改为多圆锥投影。这个投影从世界层面上来看有点怪(从图3中可见),但在地图上可见一条优美的坡度和曲线。多用些不同的投影方式是很有意思的。

图12
图13显示了另一个帅气但比较没用的地图。很容易看出加利福尼亚、得克萨斯、佛罗里达和纽约都在均值以上,而且还能知道四个人口最多的州按顺序依次是加利福尼亚、得克萨斯、纽约和佛罗里达。
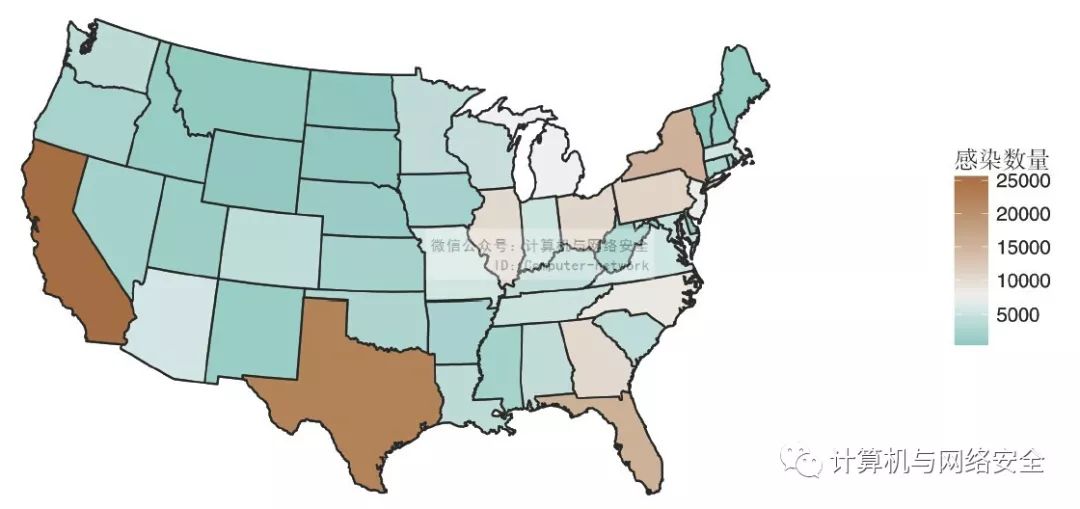
图13 美国各州的ZeroAccess木马的分级统计图
换句话说,您能看出这幅地图反映出的是人口情况,因此您要将该数据进行归一化(normalize),使之成为人口数。有很多种方法能够进行归一化。最简单的方式包括回答下面其中一个问题:
一次感染多少人?
受感染的人所占的比例是多少?
每1000人中有多少次感染?
这些问题间存在很微妙的差异,在这种情况下您会回答第一个问题,因为您可以得到整数,并且对阅读者来说更容易概念化一些。为了确定一次感染的人数,要用一个州的总人数除以这个州的感染总量。
记得加利福尼亚、得克萨斯、佛罗里达和纽约的感染量是最高的吗?使用图14中生成的za.norm数据,可以看到确切的数量。当您对人口进行归一化时,加利福尼亚和纽约低于均值,平均每1440和1287中感染一次(参见图15)。怀俄明州因每724人中就有一个受到ZeroAccess感染而成为受感染最多的州。
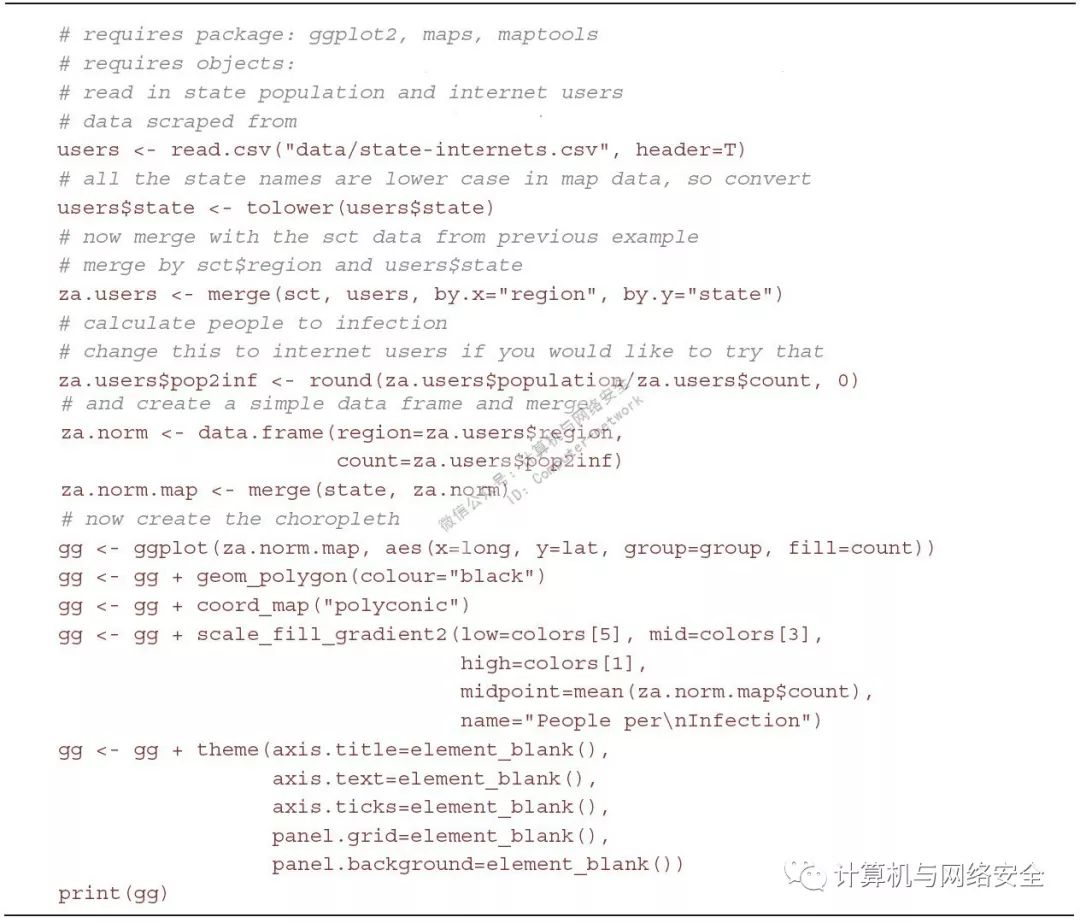
图14
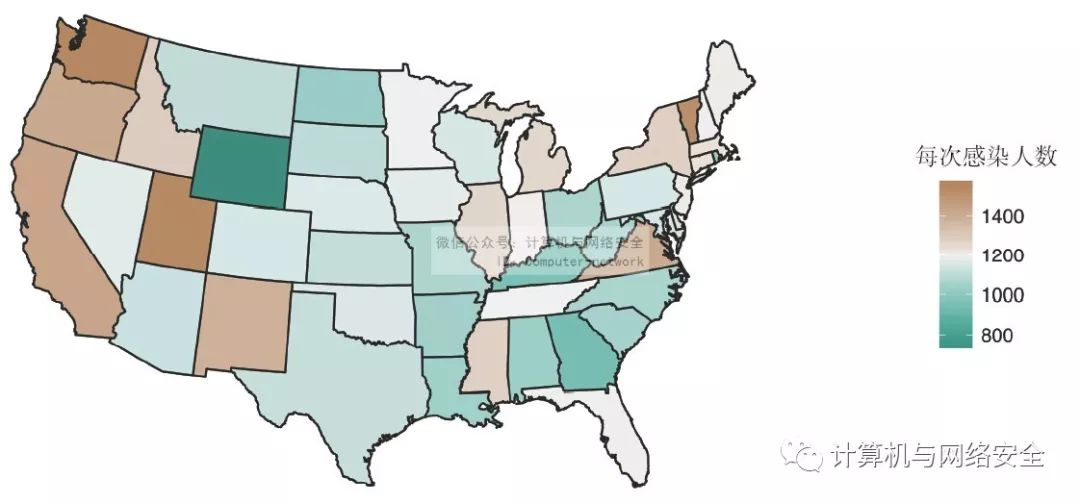
图15 归一化后的ZeroAccess木马感染情况:每个州的每次感染人数
在state-internets.csv文件中还包含了互联网用户的数据,可以试着创建一幅分级统计图来表现每个州的估计互联网用户的归一化(这幅图将更加好看)。
4、结果奇怪吗?
让我们停下来看看目前的结果。得到了一系列归一化后的值:从怀俄明州的724人中感染1人到华盛顿特区的1550人中感染1人。这难道意味着怀俄明州的人们比华盛顿特区的人们更草率、更不小心?也许更多的华盛顿人用的是?或者,一个更重要的概念是观察范围是从测量准确度的自然变化以及自然世界中得来的?是因为总得有最后一名,而在这份数据中刚好就是怀俄明州,所以怀俄明州就成为了感染最严重的州?要能够区别极限值是否为离群值,或者极限值是否符合预期。有两种方法能够对离群值(outlier)进行检测:
使用箱线图(“IQR”方法)。
计算z分数。
(1)使用箱线图找出离群值
由John Tukey发明的箱线图是被设计用来直观地展示数据的分布。具体做法是从该分布的第25百分位到第75百分位之间绘制盒子。该距离被称作四分位数间距(inter-quartile range,IQR)。之后从盒子上、下沿做长度为IQR一倍半的延长线。任何超过在这些线的值即为可能的离群值,可以用点来表示这些值,越远的点就越有可能是离群值。为了创建箱线图,可以使用R图形库里默认的boxplot()函数。之后将返回的结果储存在一个叫popbox(见图16)的变量中,并在图17中进一步探索。虽然有很多种方法能够创建箱线图,但该默认函数只需要一个该分布的值的向量,之后的事情就可以交给函数去做了(见图18)。

图16

图17
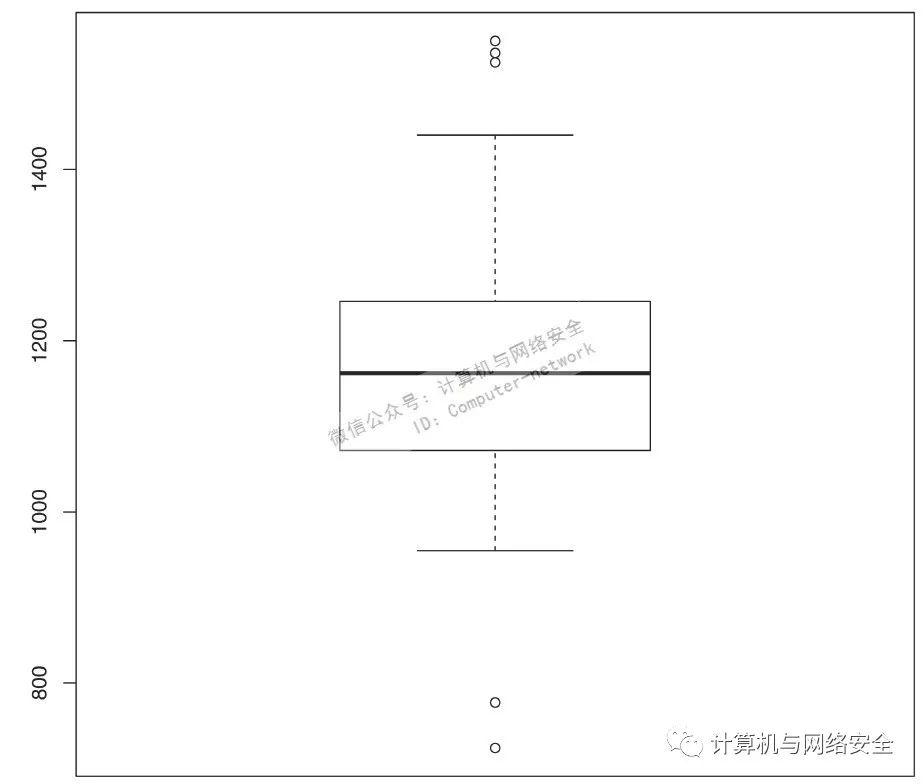
图18 全国感染的正态分布
看起来找到了几个以独立的点表示的离群值。它们中的三个在箱线图上方,两个在箱线图下方。虽然可以在za.norm中将数据排序并找到这五个离群值,但由于已经将包含着该箱线图各种数据点的boxplot()输出保存在了popbox变量中,因此也可以在原始数据中的popbox$out(离群值)向量中查找这些值(图17)。
根据Tukey在箱线图中使用的方法,可以将这五个州看做异常(即离群值)。
(2)通过计算z分数找到离群值
另外还有一种找到离群值的方式,可以计算一个叫做z分数(z-score)的值,它能通过展示一个点距离均值有多大的标准差(standard deviation)来帮您认识该点在多大程度上是一个离群值。z分数通常用于在完全不同的尺度中比较多个分布,这个方法也被叫做数据“标准化”。为了做这个计算,需要知道该分布的标准差和均值。对于分布中的每一个值,要计算其观察值相对其均值的标准差有多大。即每个值减去均值,再用标准差去除。(见图19)
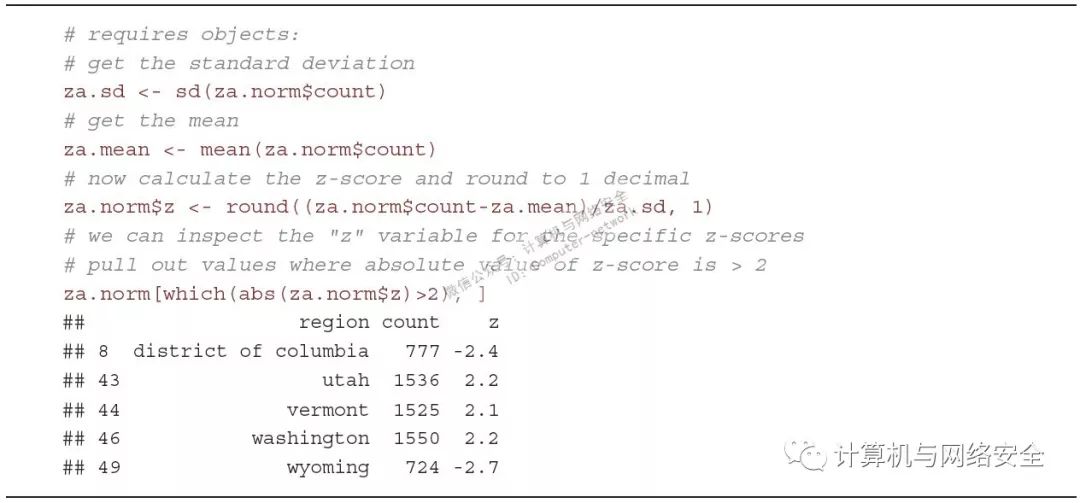
图19
如果看不懂z分数的描述,不要着急,每次计算一个数值,我们都要查阅是怎么算的。我们会将从分布中所看到的与称之为标准正态分布的“经验准则”相比较。在正态分布(常见的钟型曲线,也称作高斯分布,Gaussian distribution)中,大约分布的68%落在均值的一个标准差(上下)内,95%的数据落在两个标准差内,99.7%在三个标准差之内。
有一点要注意,如果数据偏斜,这种方法表现就不好了,因此可能要检查一下初步的直方图(把za.norm$count传递到hist()函数里)来确认偏斜不太明显。
若使用这种方法,在三个标准差以外的任何数据都被标记为典型离群值,甚至可以考虑把大于两个标准差的值作为可能的离群值。
从结果中发现5条记录都落在三个标准差以内。这个知识用于人口的归一化过程会有些疑义(也许用“互联网用户”来度量更好)。
与其聚焦于解决州一级的事情,不如把数据用于州下面的郡一级。这样做会补充更多数据点,并对总人口做一个更好的分割,来展示更多的可能性。
总的来说,考虑这些值在三个标准差的期望值内是没问题的,但是如果有时间,更细致地观察并确定衡量标准是否有效会是很好的做法。剩下的就是必须回答的问题,“这不奇怪吗?”回答是模糊的“可能不吧”或不置可否的“不那么确定”。
什么是P值?
试图识别异常(weird)和正常(normal)是统计学的核心概念,取决于具体条件,通常有多种识别方法。“统计显著性”的核心是知道某件事是异常的或者是正常变化的结果。p值是一种十分常见和普遍的方法。不要误以为它被普遍使用就是普遍理解或者甚至完全通用了。p值有它非常具体(且难于记忆)的含义。为了定义和计算p值,从声明(术语叫“零假设”,null hypothesis)开始,然后在零假设的条件下,计算数生成的概率,这就是p值。p值的细微之处经常被人忽略,人们会习惯于跳到一个容易(但错误)的假定,就好像p值是零假设为真的概率但其实不是。
如果让这个概念再复杂一些,不知什么原因,大家一般接受的是p值小于等于0.05(1/20)是“统计显著”的,本质上是任意截取的点(如果0.05不够显著,还可以规定0.02或0.01)。p值是度量显著性的方法,在这个例子中,是度量“异常性”的。
5、郡计数
概括郡(county)级比较难,因为这是非常广泛的群体。单单从标签后面看人的多样性是看不清楚的。计算一些像收入或更重要的郡级ZeroAccess感染的外星访问时会陷入困境。能够通过再一次重复latlong2map()来获取更细的粒度,仅仅在郡级。
更细致地检查IP地理故障要考虑几个补充项。大多数主流IP地理服务发布了比郡更细的准确度估计值。例如,用于此数据的服务声称对于25英里范围,只有大于4/5的记录是准确的;约1/7的记录在错误的城市。这意味着应该对这个数据警觉吗?为了回答这个问题,需要弄懂一个统计学概念:自然变化的抵消比累积更频繁,特别是当拿到更多数据时(超过3000个的郡称得上更多数据)。
变化是累积还是抵消?
在统计学里,自然的变化通常相互抵消,但这在工程领域(像计算机科学)通常违反直觉。在工程领域,人们的认识是增加有轻微变化的元素,会取得叠加效果并期望效果波及更大范围。区别是什么?哪种观点正确?
这是种复杂的概念,来举一个例子。假如您正在制造一个物体,想让它长度为100毫米(mm)。材料质量的自然变化和制作过程导致零件范围在98至102毫米之间。工程师知道,如果累计100个这样的零件,这些零件的范围会在98至102毫米之间等概率出现。意思是有可能100个零件都是98毫米,或者都是102毫米,他们预料到输出会是比较大的范围。累计得越多,输出的范围越广。
在统计学里,如果能假定每个零件在某范围内变成任意长度的可能性相同(并且想要在实际中验证该假设),长度的不同会相互抵消。幸好有对编程的基本认识,可以对这个进行建模,观察多个零件间是如何发生变化的。
下面的例子是生成100个零件,在98至102毫米间均匀地“制作”它们。然后求长度的均值(也可以求和或使用其他度量,不过这里是均值)。工程上猜测均值在98至102之间都可能出现,但是让我们来看一看结果(见图20)。

图20
运行后结果是100.0141。让我们生成由100个零件累积的10000个集合,来看看范围两端有多大(见图21)。当然如果可能,至少应该观察10000个集合中落在范围两端的几个集合。

图21
发生了什么?对100个随机零件做了10000次迭代,没有一次接近98或102附近。可以通过运行hist(parts)在快速直方图画出所有零件,可以看到以100为中心精确的对称分布。尽管零件可能都是98或者102,但是变化会抵消,尤其是集合扩大以后(除了100的集合,在runif函数里试试1000或10000)。当您在范围内加入更多零件,结果可能向均值聚集得更紧密。
在这一问题上有两点要注意的。第一,生成数据来回答“假如会怎样”这样的问题的确很有趣。第二,不该丢弃不完美的数据。如果变化是自然或随机变异产生的,可以假定这些变化更可能抵消而不是叠加。这并不意味着应该忽略这样的变化,而是告诉您变化没有您想象的那样对分析有那么大的冲击。在您的工作里仍要解释清楚变化。
从上面回到分析中,您有所有种类的可能背离计算的空间数据。所有地理检查的准确度在半径25英里内(因此,例如有些点假如落在南缅因州,最远落在新罕布什尔州)。有些数据点的误差甚至还要更大。但是如果误差是随机的,就有可能相互抵消(新罕布什尔州所有样本点的均值很可能落在缅因)。这不是说数据毫无价值。在学习了更多先进技术后,您就会对这种错误持怀疑态度了。换句话说,可以用这个数据估计外星访问有多大效果,但是您不会愿意基于分析来衡量公司的命运,至少在没有更严格的调研数据前不会。
6、郡级
为了将数据向郡级别过渡,您需要对相同的ZeroAccess数据调用相同的latlong2map()函数,但调用这个函数只是为了转换郡的名字(见图22)。需要注意的是,在有3000多个郡,这意味着您需要超过800000多组经纬度,因此,根据系统的不同,运行这段程序需要一些时间。像上次一样,您要忽略那些不属于范围内的数据(它们在数据中被设置成NA)并且要考虑到Potwin效应(只要低于国家级别都应该考虑这个效应)。这里不使用table()来计数并且把结果丢到一个数据帧里,而是必须在返回的名字上做一些转换。当那些郡的名字被latlong2map()函数返回后,是以单一文本字符串呈现在“州,郡”这样的格式中的。也可以用strsplit()函数来分割这些郡的名字,并以列表对象的形式返回。这样就可以使用unlist()函数将这个列表转换成向量,这个向量将会很长,其中州和郡的数据交替出现。不用担心,可以使用ncol=2参数将这个向量转化成一个有两列(分别代表州和郡)的矩阵,并逐行处理(而非逐列处理)。结果会与每个郡的感染量一起放入一个数据帧内。现在看看这种数据再加工的过程是多么有趣。
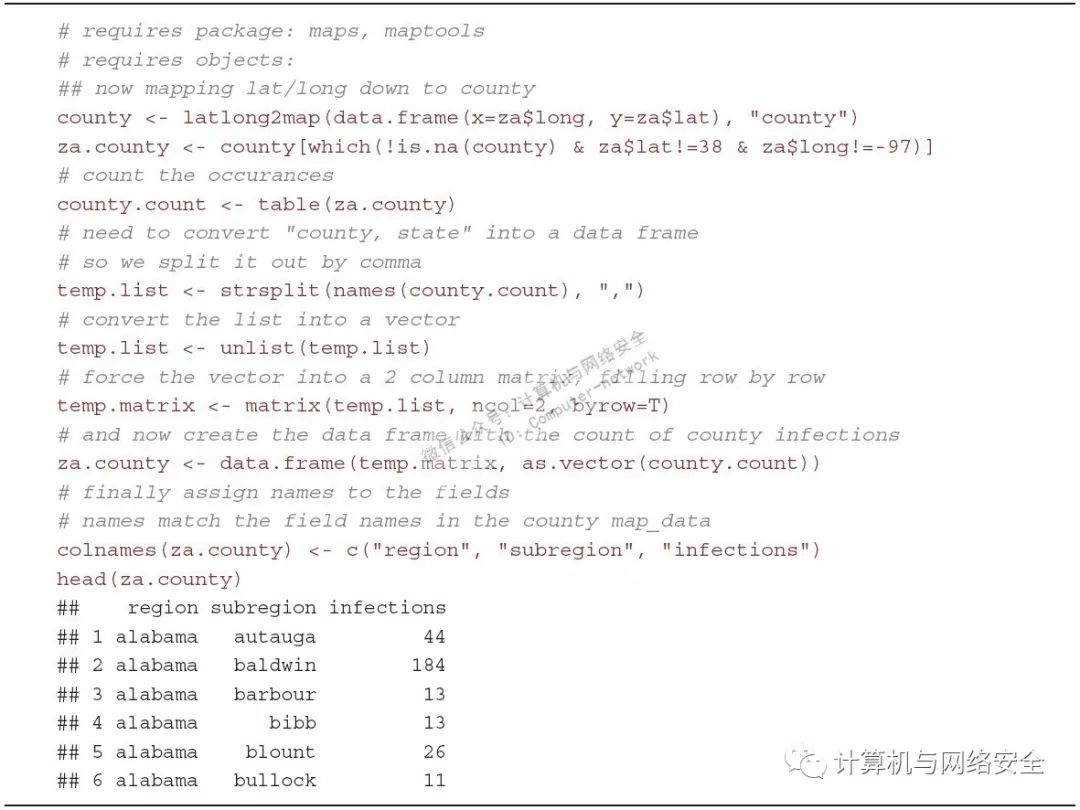
图22
现在得到一个拥有三列的数据帧:州、郡以及感染量,不要忘记给每列数据都加以命名。在进行下一步前要问一个问题:有了这些数据帧又能怎样?除了制作出一个看起来很炫的地图之外,从这些标注在地图上的原始感染量中了解不到更多的内容。或许可以看出那些感染较为严重的地区,或者对比一下各个地区的感染量,但是真的难以从地图上的这些具体数据中获取更进一步的信息。为了解决这个问题,目的不再是单纯地用这些数据制作一幅地图,而是要进行一些真正的分析,来看看是不是可以对感染量做出一个解释。
这里需要引入其他的数据(同样根据郡来划分),就像在州的级别中对人口所做的处理一样。这样也许能够对恶意软件的感染有更多的了解。也许一些外来的数据可以帮助解释恶意软件感染情况中的一些变化,或者支持那些我们想运用的技术。
我们从互联网上收集一系列有趣的数据点,然后对其进行数据再加工得到这里使用的数据。
region和subregion分别代表州和郡。
pop代表郡的估计人口数量。
income代表这个郡的中值收入。
ufo2010代表在2010年间这个郡的UFO目击次数(数据来自UFO国家报告中心:nuforc.org)。
幸运的是,这些数据可以很好地被读取,并与刚刚生成的郡的ZeroAccess数据直接合并。merge()函数有一个需要注意的地方:该函数默认会丢掉那些没有同时出现在两个数据集中的行。这样的话,ZeroAccess数据中就少了160个郡。有很多原因会导致这个结果:也许这些郡中的IP地理服务本身就不够准确,或者是一些人口稀疏的郡根本就没有发生感染。
您可以继续挖掘这些数据,但是有一点是确定的:90%未发生感染的郡的人口数量都小于10000。通过在merge()命令中使用all.x=T可以避免从x数据(第一个被传到merge()函数的参数)或者该命令的county.data(见图23示例)中丢掉任何一行。为了能表达得更清楚,在调用merge()函数的时候我们将其参数标签也包括进来。
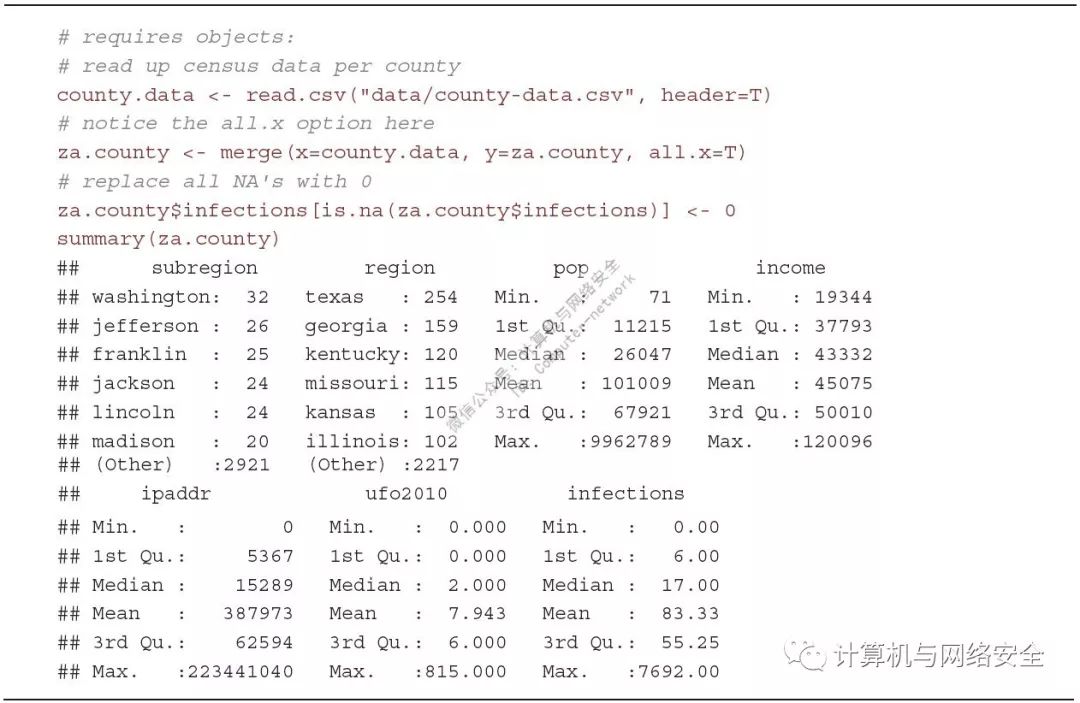
图23
当对这些数据运行summary(za.county)的时候,可以大致感觉到结果会是什么样的(并且会发现那些为郡命名的人跟郡的建立者有着非常紧密的联系)。
现在再来看这些数据,能从中找到感染量与外星访客之间的关系了吗?还没有?那么怎么才能从数据中找到关系?感谢统计学家的不懈努力,使得您可以运用一种叫做线性回归的技术,它这是一项非常强大而又相当危险的技术。
二、线性回归
回归分析是一个广泛使用的基础课题,在很多科学成果背后都有它的身影。当有人说“科学家寻求某事物与另外某种事物之间的联系时”,这基本上就是建立在回归分析的基础之上。研究人员通常会因为两个目的而使用回归分析。
首先,它可以用来估计不同的可观察输入如何导致可观察输出。例如,您想估计外星人到访(可观察输入)如何影响国家的ZeroAccess感染率(可观察输出)。使用回归分析,您不单可以估计每个变量的显著性(或缺乏显著性),还可以估计其影响的强度。如果您现在感到有点混乱,请不用担心,当您真正开始研究数据时我们会更详细介绍。回归分析在用于描述不同观察结果之间的关系时是一个很强大的工具。
第二个回归分析的用途是预测。回归分析的输出是一个公式。给一个特定的输入,您就可以估计或预测输出。一个经典的例子是身高和体重的关系,通常会认为较高的人都会比较重,但如果添加了其他变量,例如性别、年龄等,就可以确定一个期望值,并划出一个人可能的体重范围。这也正是医生告知病人他们是超过了还是低于他们的期望体重、身高等的方法。回归分析在估计和对比观察到的输出时是一个强大的工具。
为了展示这两个用途,要建立虚构(而且非常简单)的数据。从一个单一输入变量开始,然后用正态分布生成随机数据点(任何分布都行,正态分布只是比较好看)。然后使用rnorm()命令并建立200个数据点,其均值和标准差分别是10和1(即默认值),见图24。

图24
在图24的summary中,看到的是范围在7.2与12.9之间的数据。现在需要生成输出数据。想要创建的是输入和输出之间的一种线性关系,因此将均值作为输入变量的两倍传入。而在使用rnorm()时引入了更多的随机变化,从而得不到完美的线性关系,但是通过将随机性(即均值)置于输入变量的中心,就可以创建足够的线性关系用于建模。之后就可以从输入和输出中创建一个数据帧以便于处理和绘图。
有了输入和输出,就可以把所有这一切传给ggplot(如图25所示)并创建一幅散点图来可视化它们之间的关系。现在通过geom_smooth()函数并让它使用线性模型“lm”来添加一些特别的东西。这将在散点图之上叠加一条能够很好地描述输入与输出之间关系的直线。

图25
你可以从图26中看到,数据并不是很整洁(这就是rnorm()引入的随机变化造成的),但是能从其中看到一个确切的趋势。随着输入变量的增加,输出变量也随之增加,数据由左下流至右上。看起来这中间的确存在着某种关系,但却又难以言表……由此进入回归分析。
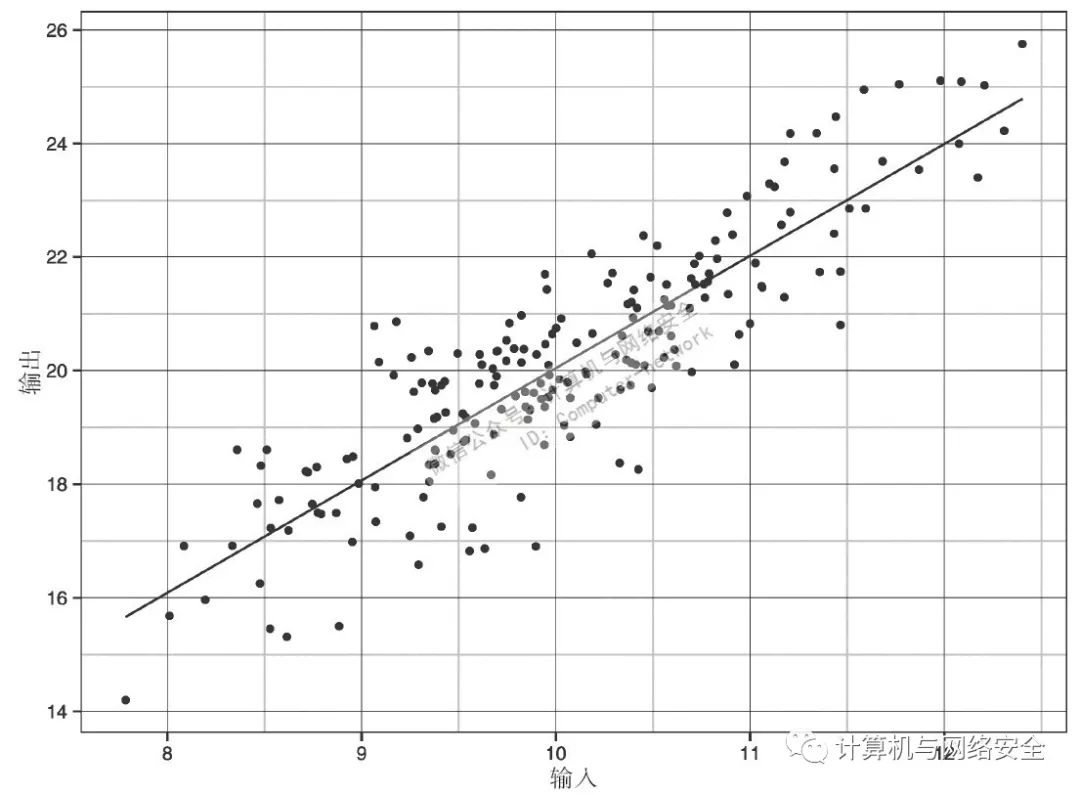
图26 采样数据与回归线
要为数据应用线性回归,只需要一条非常简单的命令(如图27所示):
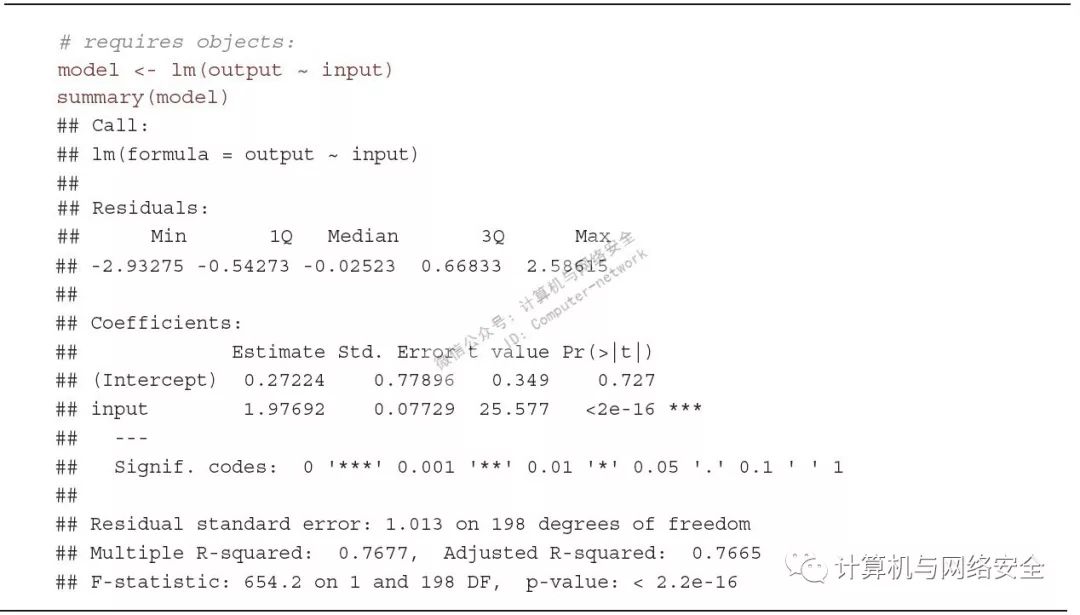
图27
这里有很多很多需要研究的东西。这段程序由您使用(“Call”)的函数和对残差(residual)的总结开始。残差指的是这个模型做出的预测与实际看到的输出之间的差异。这一行被特别计算过因此残差的均值是零(这也使得它成为“最佳匹配”数据)。通常我们跳过残差这部分,因为有很多其他的更好的办法来解释残差。
之后是关于系数的部分。在这个模型中有两个系数,截距(intercept)和输入变量(input variable)。如果有更多的观察输入,都会被列出,每个输入一行。第一列是该系数的估计值。对于大多数线性模型来说,截距几乎没有(甚至完全没有)意义。这里的截距系数表示如果输入为零,则可以估算输出值在0.27左右(比如当讨论的是一个人的身高时,就没什么实际意义了)。这个不是我们创建数据时(设置为0)所设置的,因此0.27还是很接近的。
通过这些系数,可以构建模型:
output=0.27224+1.97692×input
当给定一个可观察输入时,可以使用这个模型估算输出值(或者只使用predict.lm()命令传入模型和新的输入变量,以进行预测)。但是要记住是通过将输入乘以2来生成的数据。而这里的线性模型则认为乘以了1.97692(这很接近)。这个系数让您在做输入变量推断时能够领略到回归分析的强大,而这只是一个开始。可以这样理解:
如果所有其他输入变量都保持不变,输入变量一个单位的变化对应的输出的平均变化为1.97。
因为只有一个输入变量,没有其他变量可以保持不变。而即使您有很多变量,也可以使用回归分析将单个变量的影响效果隔离出来。在后面,将会回到ZeroAccess的感染数据上,并使用这种方法推测外星访问对于感染的影响。
系数中的下一列表示的是标准误差。可以把它与估算系数一起使用来生成一个置信区间。另一种做法是将lm()的输出传入confint()函数(如图28),这样置信区间就会被自动计算出来。

图28
输出告诉您,在有95%置信的情况下,输入系数在1.82和2.13之间(2的值同样也在这个范围内)。
之后的两列是变量对于模型影响程度的度量。最后一列叫做p值。作为一种化简,较小的p值对于模型的总体影响更大,而较大的p值意味着输入和输出变量之间的关系偶然性更大。当有一个较高的p值时,应该寻找其他解释性的变量,并去掉任何有着较高p值的变量。
大多数人都会选则0.05作为判定一个变量是否显著的阈值。这意味着如果p-value小于0.05(此例中的p值小于0.05),这个变量就是应该保留在模型中的重要变量。而当您的p-value大于0.05,就应该考虑将该变量丢到一边去。使用三个不同的显著性阈值(0.1、0.05和0.01)来评估p-value已经成为一种惯例,因为这样可以让模型具有一定的灵活性,并且减少截点选取的截断性这种方法通常在学术刊物中常用。可以从图27中的模型输出中看到p-value是根据哪一级的显著性阈值来进行评估的(在本例中是0.001)。
另外,线性回归的输出中还有两点需要考虑。看一下图27倒数第二行里的Adjusted R-squared值。Adjusted R2(学术上称为校正后决定系数,adjusted coefficient of determination)表示的是模型解释的变化总量。取值范围为0到1,0意味着这个模型不比直接使用输出均值更好,1意味着这个模型能够完美地描述输出。它在这个模型中计算出的值是0.76,这意味着这个线性模型能比较合理地解释输出数据中76%的变化。决定系数R2是相对的,因此不要将它作为一个神奇的数字。如果只想单纯猜测输出(就是说不能解释输出中的任何变化),那么为R2取0.05会更有帮助。但如果已经有了一个0.76的模型,那么取0.05就相当于退后一大步。
当人们想要快速理解一个模型的时候往往会关注R2的值。
最后要考虑的是图27最后一行中的p-value,这是整个模型的p-value。这时您大概已经能够感觉到这到底是不是一个好的模型,但还是要留神这个p-value。在本例中,这个p-value非常小,因此您应该对这个模型有信心。
1、回归分析中的常见陷阱
(1)不能脱离数据去推断
数据代表了您的知识范围。可以验证数据中存在线性关系,但不能认为输入值以外的其他数据上也存在这种关系。例如,您建立了一个简单的模型用来根据记录丢失的数目(输入)来估算数据外泄所造成的损失(输出)。如果仅研究了由丢失1000到10000条记录所造成的数据外泄,那么就不能将这个模型中得到的结论用于由丢失多于10000或少于1000条记录的情况。不能确定在您研究的数据之外这种关系依然成立。(即使真的建立了这样一个可笑的模型,也必须讨论R2值非常小的原因,这样大家基本会摒弃这个模型。)
(2)离群值的影响
在进行回归分析之前,应该先去核实数据的有效性,并且找出由错误导致的离群值。离群值对模型的输出及模型选择都有很大影响。这并不是说您要删除一切非常规观察值(尽管这是通行多年的做法)。如果很多观察值看上去都像是离群值,比较好的做法是在继续下一步之前先确认它的有效性。有些离群值是有效的,此时就必须把它们纳入模型中。而如果离群值是因为输入错误或者使用不同度量单位而错误导致的,那么应该将它们修复或删除。
(3)隐藏关系会很隐蔽
将一堆变量一起丢入线性回归中并发现它们中的很多都是显著变量,这件事并不难。但需要用一些常识去看待这些关系。将变量数目降到最低是最基本的做法(见下个陷阱)。但是数据的内在关系有可能会误导您,而且您要小心多重共线性(multicollinearity)。如果您的输入值存在两个或两个以上相关性很高的变量,那么极有可能错误地给它们赋予了不存在含义。
(4)变量过多
如果您将足够多的变量丢入回归分析中,那么它们之中必然会存在明显的关联。其实这同样适用于很多回归分析之外的概念。之所以会得出这种具有误导性的结论是因为随着加入模型中的变量越来越多,产生这种伪关系的可能性(由巧合产生的统计显著相关性)也越来越大。如果回归分析很复杂或者在没有领域专业知识的情况下进行分析,这种效果就会加剧。在线性回归中的一个很好并且常见的做法是找出最小的输入变量集合。而为了简化而排除那些只能稍微改进模型的变量也是很常见的做法(即使该变量的p-value很小)。这同时也引发了对于过度拟合的讨论。过度拟合指的是模型在原始数据上运行得很好,但在真实数据上表现很糟的情况。
(5)可视化及使用吸气测试
在开始回归分析之前先对数据进行肉眼审查是个不错的注意。在本例中,创建了一个简单的散点图并添加了回归线。当加入多元变量的时候事情会变得有些复杂,但这是个好习惯。即便如此,依然希望能够用合逻辑的合理数量的变量确保有理由将它们考虑进来。这么做有助于减少变量总数,同时能帮助分析师更好地理解数据,如果他们之前没做过的话。
2、ZeroAccess木马感染的回归分析
您应该对回归模型以及在使用它的过程中可能出错的地方有了一个基本的理解。现在可以开始从空间数据中发掘出比使用地图所能得到的更多的含义。
现在让我们用真实数据做一次回归分析,看一看“外星访问”是否能描述ZeroAccess的感染情况。虽然这对于不相信外星生命的人来说是件很傻的事,但我们作为研究人员应该对可能性持开放的态度。我们没能找到关于外星访问的切实数据,但国家UFO报告中心的人们收集了各种外星人目击事件。您将要用这份数据作一个代理,它在事先准备好的ufo2010变量中。为了执行线性回归,您要再次调用内置的lm()函数并指定输出变量(za.county数据帧中的infections),然后是波浪号后面的代表外星人目击数的变量(参见图29)。如果想要添加更多变量的话可以用加号(+)来添加它们。如果使用summary()将整个命令包裹进去,您会立即得到输出,而输出已经被裁减到只剩下相关信息。

图29
通过新掌握的技能,可以看到UFO变量的p值非常小(<2e-16)。这表示连接关系非常显著,并且R2为0.74。这让人印象深刻。UFO目击事件的系数(8.31867)表明每一次目击事件都伴随着8次ZeroAccess感染。这是一个强有力的模型,它让您有了足够的材料递交一篇论文说明您已经科学地证明了ZeroAccess是由UFO引起的!我们上了头条新闻:
研究人员将ZeroAccess感染与外星人联系起来了
不过不要操之过急,也许应该看看其他的变量。虽然我们对添加太多变量很谨慎,仍然需要研究这些关系以及各种模型。现在要用所有的变量再执行一个回归分析,看看会发生什么(参见图30)。

图30
尽管有该模型的所有变量,也应该考查我们前面讨论过的多重共线性变量。即两个或更多输入变量相关且他们的关系掩盖了变量的(非)显著性。这通过观察一个叫做方差膨胀因子(variance inflation)的参数来考查。在R的应用回归指南(Companion to Applied Regression,CAR)包里有个不错的vif()函数(参见图31)。一般情况下,若方差膨胀的平方根大于2(每次必定检查这个),这些变量就是相关的,不要指望它们都对模型有显著贡献。

图31
能看出人口和ufo2010是共线的。哦,不!有没有可能UFO目击量只是人口所产生的影响?为了测试这个,将人口数标准化。这样做,仅用人口去除这两个值,求人均感染率和目击率,返回单回归(参见图32)。
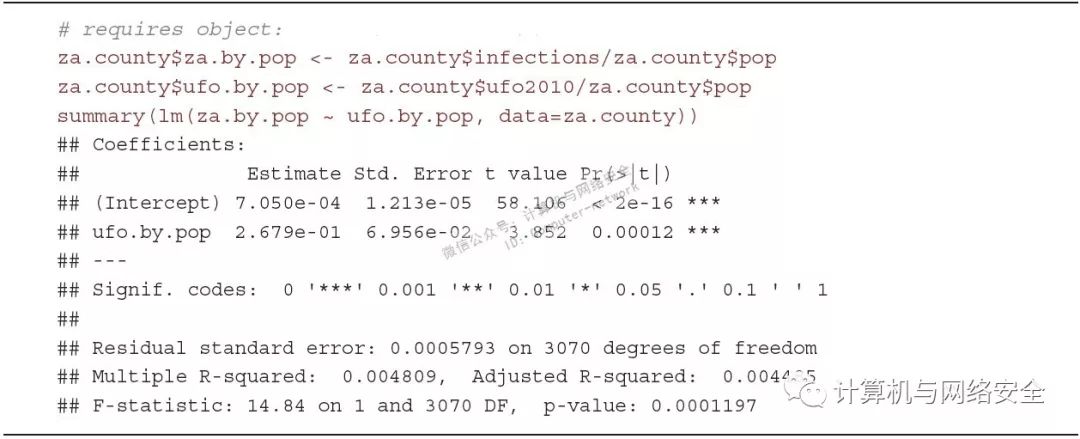
图32
非常好!p值仍然小于0.05!但是……呃……稍等,R2值告诉我们这个模型完全没用,因为它描述了数据的0.4%(R2=0.004)。在这点上,最好是听从逻辑的微小声音,总结出UFO访问和ZeroAccess感染无关。
什么与ZeroAccess感染有关?
您会严重怀疑一个郡的人口数是总体上最好的关于郡内发生感染数的预测器(Predictor,参见图33)。
图33
回到地图上看看是否可以把郡级的情况可视化。可以生成一个郡级的感染数和人口数分级统计图。如果回归分析正确,应该能看到两者之间非常清楚的关系(参见图34)。
图34 ZeroAccess感染数和人口数的关系显示
三、结语
在本文您已经创建了包括点图和分布图在内的不少图形。尽管您能通过可视化表示迅速找出图中的变化,但对于空间数据不要仅仅依赖于可视化。虽然图形显示了变化,但通过线性回归展示了人口数很大程度上解释了变化的原因。这是创建图形时(或就此而言其他的可视化方法)要考虑的。一定要不断回顾并问一个永不过时的问题:“那又怎样?!”如果您不能回答这个问题,那么也许您根本不需要图形,而需考虑一个不同的方向。
ID:Computer-network
以上是关于安全数据分析:数据点—地图—线性回归的主要内容,如果未能解决你的问题,请参考以下文章
使用 scikit-learn 训练线性回归模型后,如何对原始数据集中不存在的新数据点进行预测?