机器学习之旅分享4 | 稀疏连接的张量神经网络

Posted 2021-04-26 平安寿险PAI

· 小PAI导读 ·

本文为平安寿险AI团队SAIL Lab负责人杨海钦博士与电子科大合作在Neural Networks（JCR一区，近5年影响因子6.864）上发表的一篇论文——Block-term Tensor Neural Networks [1] （稀疏连接的张量神经网络）。文章主要通过用稀疏连接张量替代深度神经网络的全连接层，在保留甚至可能提升模型的数据表征能力下，减少模型的训练时间、存储成本和计算成本，从时间、空间和资源上改善深度神经网络模型的训练和推断。

此前杨海钦博士带来的分享包括：

欢迎大家阅读回顾。

文章作者

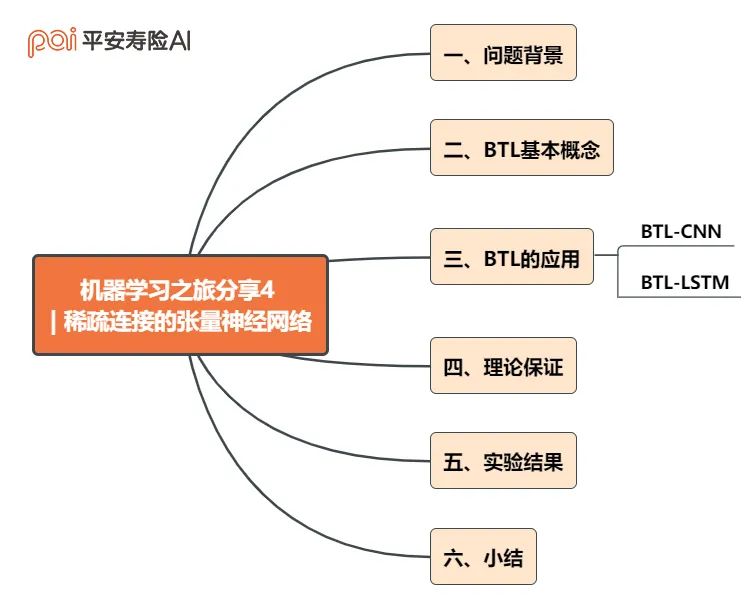
全文框架概览

一、问题背景

稀疏连接的张量神经网络（Block-term Tensor Neural Networks）是指将稀疏连接的张量层Block-term tensor layer （BT-layers）应用于神经网络中，目的在于保留甚至提升模型的数据表征能力下，大大减少深度神经网络 (DNNs)的模型参数。从而在不影响甚至提升模型效果下，减少模型的训练时间、存储成本和计算成本，从时间、空间和资源上改善神经网络模型的训练和推断。

 

背景：2012年ImageNet Challenge获胜的AlexNet模型包含了5个卷积层和3个全连接层，共计约6千万的参数量[2]。这导致该模型在GPU上需运行数天并耗费大量存储空间，其中神经网络还存在冗余的参数，在训练时阻碍了模型找到局部最优解 (local optimal)。因此减少模型参数量相当于减少了模型训练的时间复杂度和空间复杂度。低秩逼近技术是一个有效近似神经网络的方法，它不但不会降低模型效果，还可以减少模型参数量。目前研究人员主要聚焦在两个方向对该技术进行图谱：

 

1. 加快训练深度神经网络的卷积层

2. 用张量层代替全连接层，减少冗余参数

 

本文我们主要聚焦于第二种方向。我们借鉴稀疏连接的张量表征 (Block-term Tensor decomposition, BTD)[3] 和用 BT-layers 代替深度神经网络的全连接层来改善模型。由于BTD 用低秩逼近的方法结合了CP分解 (Candecom/Parafac decomposition)[4] 与Tucker分解 (Tucker decomposition)[5], 它融合了两者的优势，令其比张量分解 (Tensor train composition) 更具有稳定性。

二、BT-layers

我们提出的BT-layers的基本概念是用更少的参数逼近原本的向量乘积 并保留其数据表征能力。具体而言，我们是通过低秩BTD的技术，即用一系列的低权重小张量的乘积来复原向量乘积 。

 

下面简单介绍下张量。

张量(tensor)：

向量：一阶张量

矩阵：二阶张量

-阶张量： ,  表示相关长度

图1 张量的可视化  

张量缩并(tensor contraction)：

二阶缩并：假设 ，对 和  做运算，公式如下：

三阶缩并：假设 ，对 和  做运算, 公式如下:

结果为四阶张量 。用  表示在第 维度进行张量缩并。

多维度缩并：假设 且  ，结果如下：

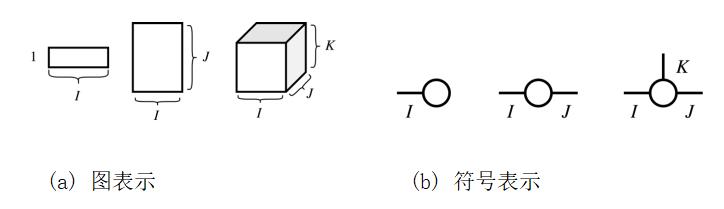
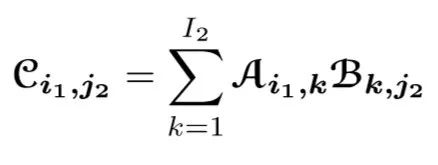
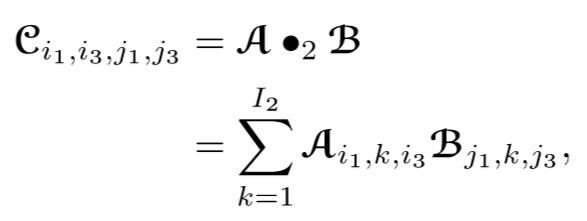
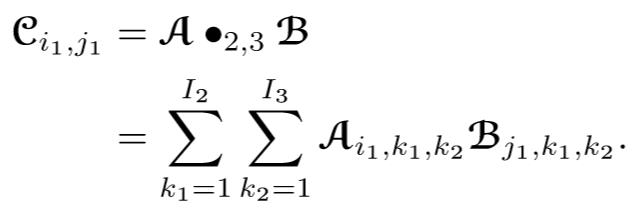
多个张量之间可以进行多次张量缩进运算直到不具备缩并条件。

 

接着我们将以上的知识运用在BTD上，我们介绍过

BTD = CP decomposition + Tucker decomposition

- CP decomposition：将高维张量分解成为Rank-1张量

- Tucker decomposition: 将一个张量分解成一个核张量与每一维矩阵的乘积

BTD结合两者的优势，将张量分解成具有低秩特性的多个Tucker模型的和：

 

图2 BTD可视化

上图中, 代表 -th Tucker模型的 阶核心张量，而每个 代表在 -th Tucker模型中的 -th因子矩阵.  也可以用以下公式计算:

然后根据以下4个步骤，我们可以使用BTD去逼近原本的全连接层( )：

1.张量化权重 和输入向量  ，得到高阶张量 与  ;

图3 张量化和反向运算

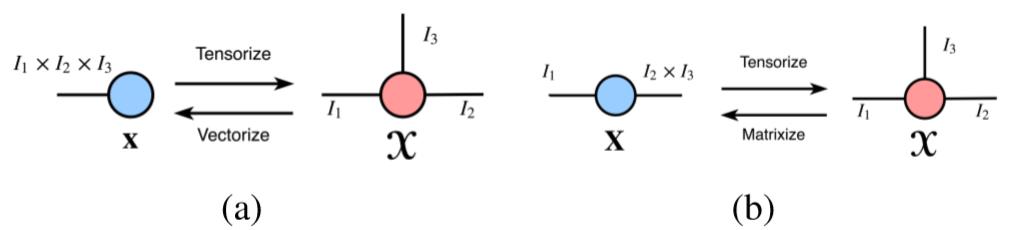
2.用BTD重构权重张量

在这里核心张量 是 维的， 表示 Tucker-ranks. 为排除权重分享不平衡, 假设 . 因子张量  相当于输入和核心张量。为了得到低秩分解，须满足 (and  ),  .

3.之后，便可以用 替代

表示会进行 维缩并. 为区分该新运算方法和全连接层，我们将之称为Block Term Layer (BTL), 如图所示：

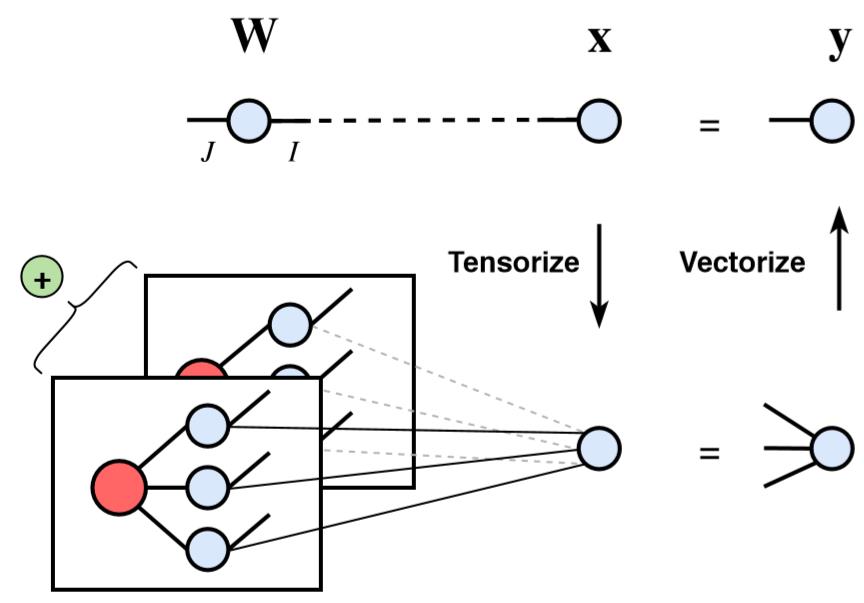
图4 BTL运算过程

4. 使用反向传递算法(BP algorithm)[6] 重构模型，公式如下：

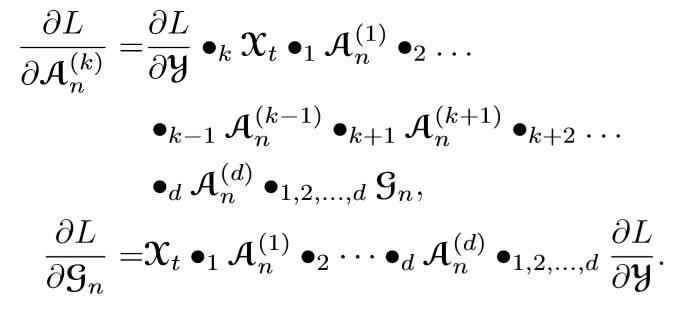
三、BTL的运用

BT-CNN

在传统的卷积神经网络中，从堆叠的卷积层输出的特征是直接馈入全连接层和激活层，它们是用作非线性分类器。为了证明BTL的有效表现，我们将BTL直接替换所以的全连接层，从而构建低秩的分类器。

 

图5 用BTL代替FC layers

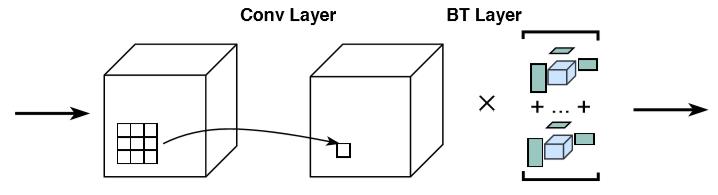
BT-LSTM

之所以将BTL运用到LSTM中是因为它是最常见的RNNs模型，当然其他RNNs 的变种例如：GRU也可以运用BTL。下图所示， ,  ,  与  都有着类似的计算操作, 所以我们直接将  ,  ,  和  叠加成  , 以  表示。

 

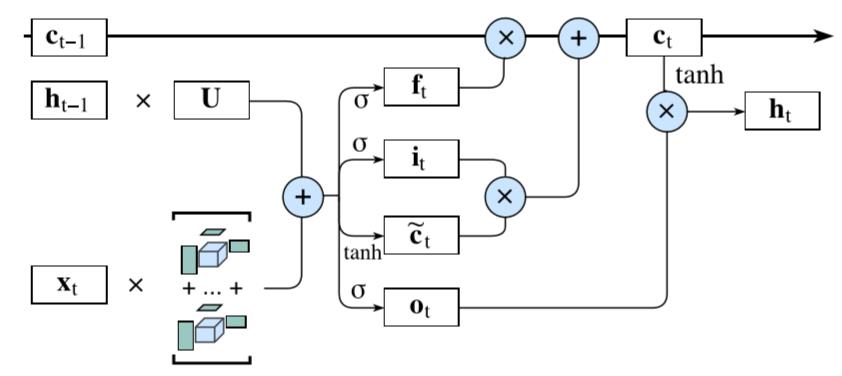
图6 BT-LSTM结构

公式如下：

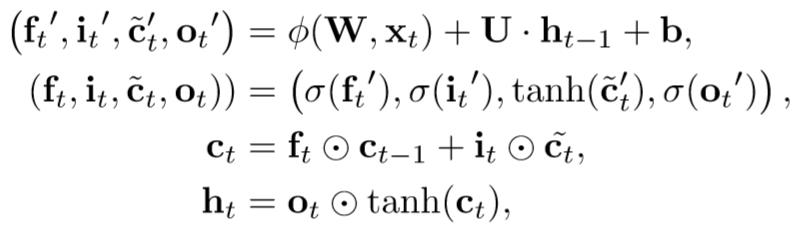
四、理论保证

我们提出BTL的压缩比例：

以上为我们的BTD参数数量，而全连接层的参数数量为 ，所以参数压缩比例为：

调参导致的参数数量变化如下图：

 

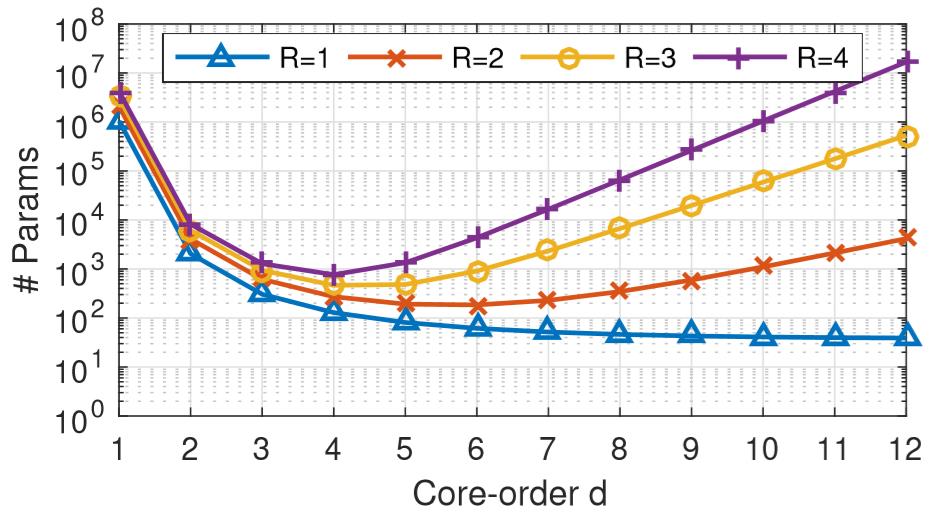
图7 Core-order表示输入张量和核心张量的阶数， =1(FC layer)

参数会随着R的增长而呈指数级的增长，所以为了获得低阶的模型，设 . 同时  ，所以R的数量有所限制，这减轻了调参的难度。从结果可看，我们选择 。

复杂度：

 

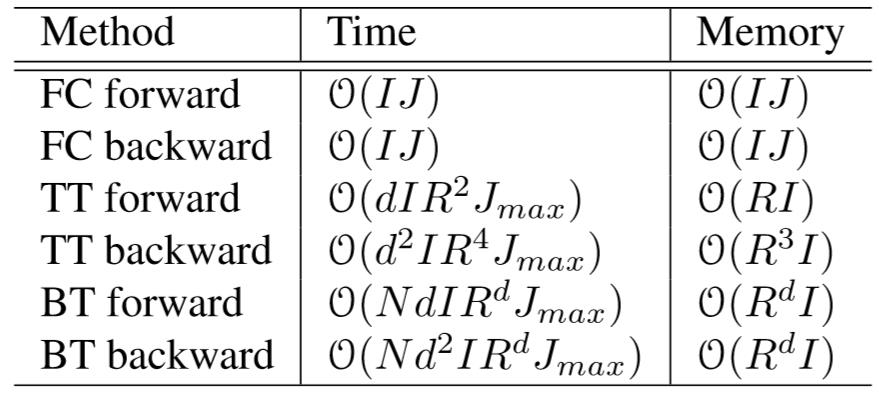
五、实验结果

论文对BTL进行了实验验证，基于3个数据集：MNIST[7]，Cifar10[8] 和 ImageNet[9] 对BT-CNN和BT-LSTM都进行的验证与对比。该实验在1个NVIDIA TITAN Xp GPU的服务器上运行。为了达到公正对比，我们训练的神经网络都是基于动量为0.9的随机梯度下降，而在每一个BT-layer后都会进行批量归一化防止梯度消失或爆炸的问题。

BT-CNN评估

以下结果是基于LeNet-5[10]模型

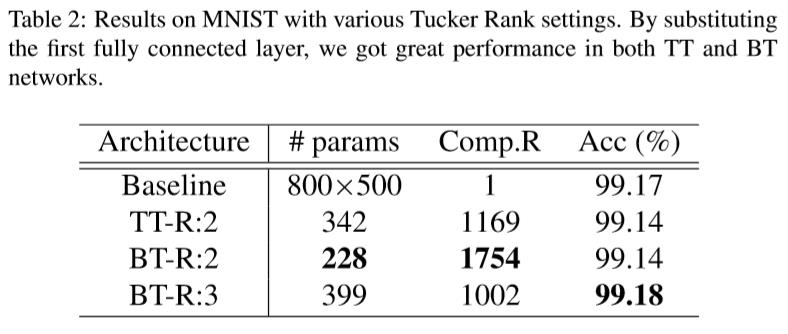
图8 MNIST结果

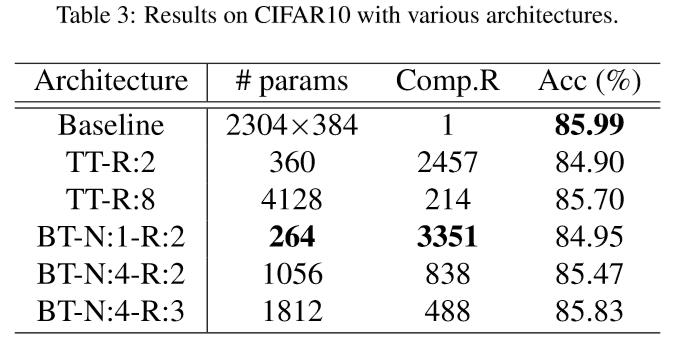图9 Cifar10结果

图10 ImageNet结果

 

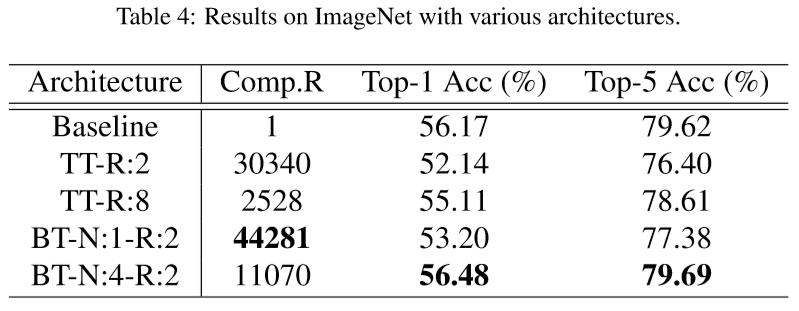
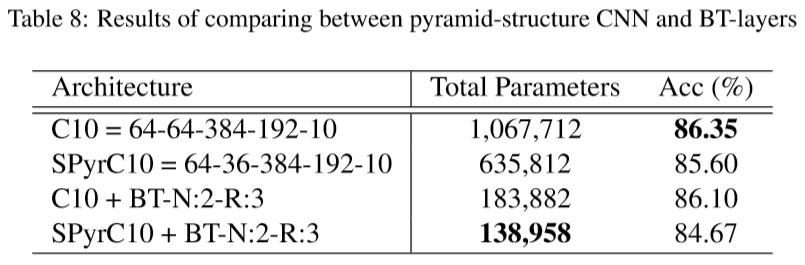
图11 对比原本CNN与BT-layers

 

BT-LSTM评估

以下结果是基于LSTM[11]模型

 

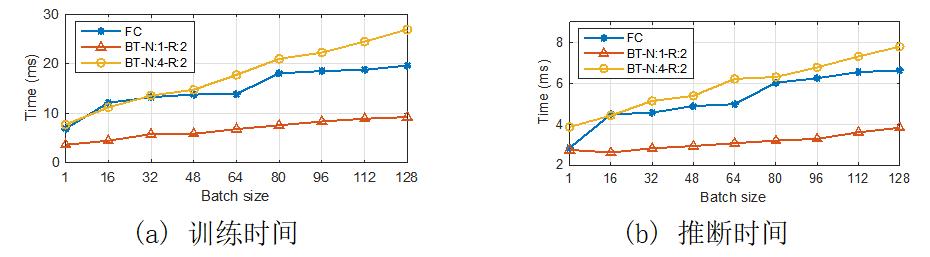
图12 运行时间对比

 图13 准确度对比

Quantitative评估 (视频分类任务)

 

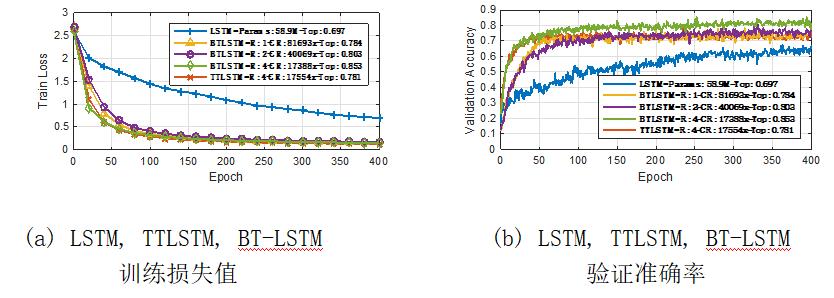
图14 任务结果对比

Qualitative评估 (图像捕捉任务)

 

图15 任务结果对比

小结：

本文我们设计了一个新型的网络结构，通过BT-layers替代CNNs和RNNs常用的全连接层。该网络结构不仅可以大大减少模型的参数量，还具有更好的数据表征能力。特别在循环神经网络(RNNs)，该结构整体改善了模型的表现能力。我们在不同数据集上的实验结果都展现了BT-layers对CNNs 和RNNs的效果具有提升。未来，我们还可以将BT-Nets结合其他的压缩技术，进一步提升模型效果。

SAIL Lab介绍

杨海钦博士为平安人寿AI团队启航实验室（Statistical Artificial Intelligence and Learning Lab, SAIL Lab）负责人。SAIL Lab以统计学习为主要手段，积极探索前沿技术，推进技术创新，打造数据赋能的启航引擎平台SEED （SAIL Engine Empowered by Data）平台, 实现在自然语言处理、推荐系统、计算机视觉等领域的落地应用，在团队中作为技术源动力，孵化新技术，引领技术革新。  目前主要提供2大服务：在线服务（寒暄引擎）和离线服务（生成引擎）。

SAIL Lab小广告：

1. 招聘优秀实习生：旨在NLP、机器学习等前沿技术研究（扫码查看岗位详情）

2. 杨海钦博士亦作为ICONIP’20的程序委员会主席给该会议打个广告，欢迎大家关注并参与亚太神经网络学会支持的ICONIP’20会议，会议链接：http://www.iconip2020.apnns.org/

---

# 机器学习之旅系列 往期回顾 #

---

References

[1] Jinmian Ye, Guangxi Li, Di Chen, Haiqin Yang, Shandian Zhe, and Zenglin Xu.  Block-term Tensor

Neural Networks.  Neural Networks.  Accepted.  2020.

[2] A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification withdeep convolutional neural networks, in: F. Pereira, C. J. C. Burges, L. Bottou, K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems 25, 2012, pp. 1097–1105.

[3] L.  De  Lathauwer,    of  a  higher-order  tensor  in  block terms—part  II:   Definitions  and  uniqueness,  SIAM  Journal  on  Matrix Analysis and Applications 30 (3) (2008) 1033–1066.

[4] J. D. Carroll, J.-J. Chang, Analysis of individual differences in multidimensional scaling via an n-way generalization of “eckart-young” decomposition, Psychometrika 35 (3) (1970) 283–319.

[5] L. R. Tucker,  Some mathematical notes on three-mode factor analysis, Psychometrika 31 (3) (1966) 279–311.

[6] P. J. Werbos, Backpropagation through time: what it does and how to do it, Proceedings of the IEEE 78 (10) (1990) 1550–1560.

[7] Y. LeCun, The mnist database of handwritten digits, http://yann. lecun.com/exdb/mnist/.

[8] A. Krizhevsky, G. Hinton, Learning multiple layers of features from tiny images.

[9] J. Deng,  A. Berg, S. Satheesh,  H. Su, A. Khosla,  L. Fei-Fei, Imagenet: large scale visual recognition competition 2012 (ilsvrc2012) (2012).

[10] Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, Gradient-based learning applied to document recognition, Proceedings of the IEEE 86 (11) (1998)

2278–2324.

[11]  J. Ye, L. Wang, G. Li, D. Chen, S. Zhe, X. Chu, Z. Xu, Learning compact recurrent neural networks with block-term tensor decomposition, in: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018. 

# 近期热招岗位 #

·  算法工程师（搜索/推荐）

·  前端开发工程师（ios/android/RN）

·  AI产品经理

……

扫码查看更多详情

# 往期精彩回顾 #