支持向量机

Posted 2021-04-26 桂和杯大数据建模大赛

了解支持向量机

支持向量机，因其英文名为Support Vector Machine，故一般简称SVM，它是一种二类分类模型，是一种监督式学习的方法，可广泛地应用于统计分类以及回归分析。

我们把事件用特征空间中的点表示，分类问题是我们需要确定一个界（分类超平面），把点分隔开来。支持向量如图所示，即离分界面最近的点。图上看来像是这些点支持起来了分界面。我们在确定分界面的时候也重点考虑这些支持向量。

算法原理—寻找最优超平面

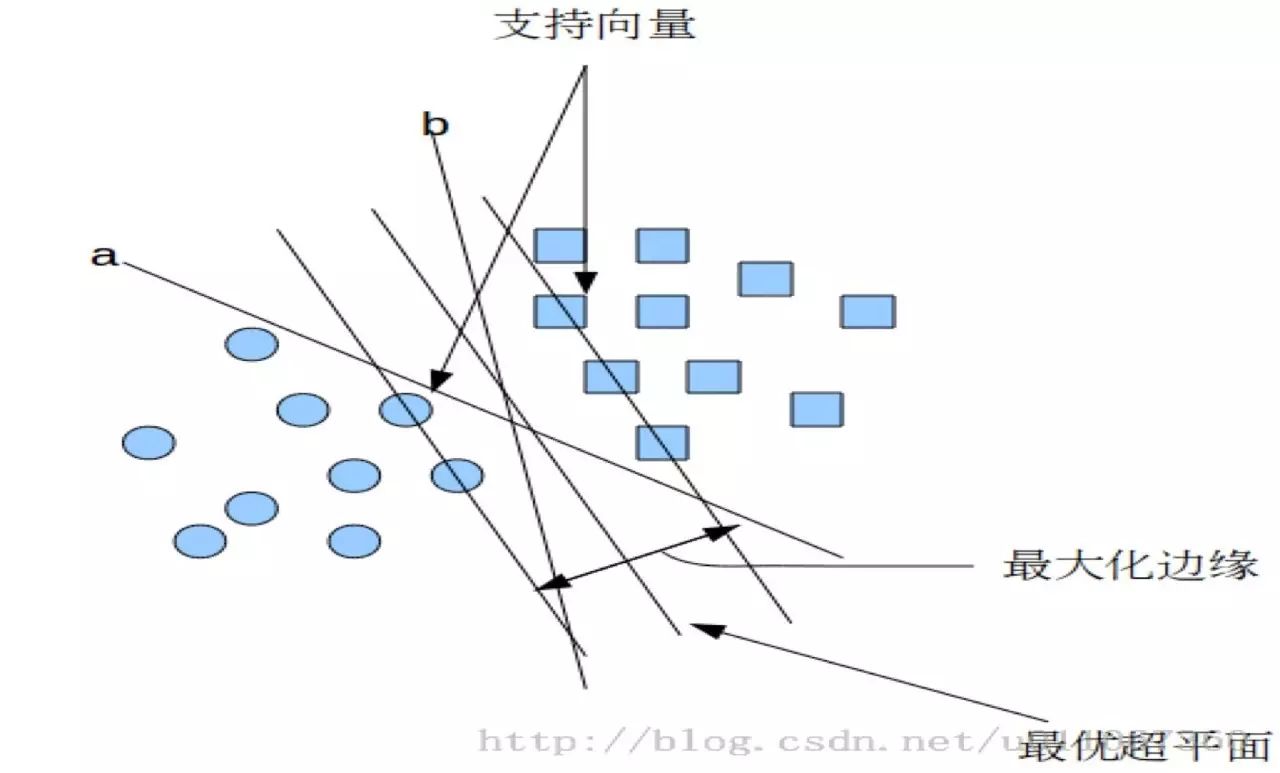
在上面的图中，a和b都可以作为分类超平面，但

有优劣之分。b是优于a的。因为样本一旦有点噪声干扰，位置稍一偏移，根据a超平面就有可能被错误划分成另一类，a对噪声敏感度高，泛化性较差。 

所以我们对超平面的评价标准是：

这个超平面距离所有训练样本的最小距离越大，则该超平面越好。我们定义间隔（margin）为平面距样本最小距离的二倍，也就是间隔越大越好。

那么应如何求解最优超平面呢？

最优超平面的计算

1.线性可分问题

我们通常希望分类的过程是一个机器学习的过程。这些数据点并不需要是二维空间中的点，而可以是任意n维空间中的点。我们希望能够把这些点通过一个n-1维的超平面分开，通常这个被称为线性分类器。有很多分类器都符合这个要求，但是我们还希望找到分类最佳的平面，即使得属于两个不同类的数据点间隔最大的那个面，该面亦称为最大间隔超平面。如果我们能够找到这个面，那么这个分类器就称为最大间隔分类器。

我们以一个二维空间中的分类为例：

超平面在二维空间中是一条直线。

用分类函数表示就是：

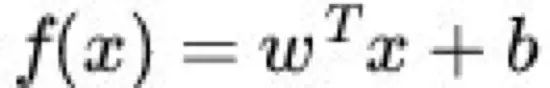
显然，如果f(x)=0,那么f（x）位于超平面上。我们不妨要求对于所有满足f(x)<0的点，其对应的 y 是-1, f(x)>0的点，其对应的 y 是1。如下图：

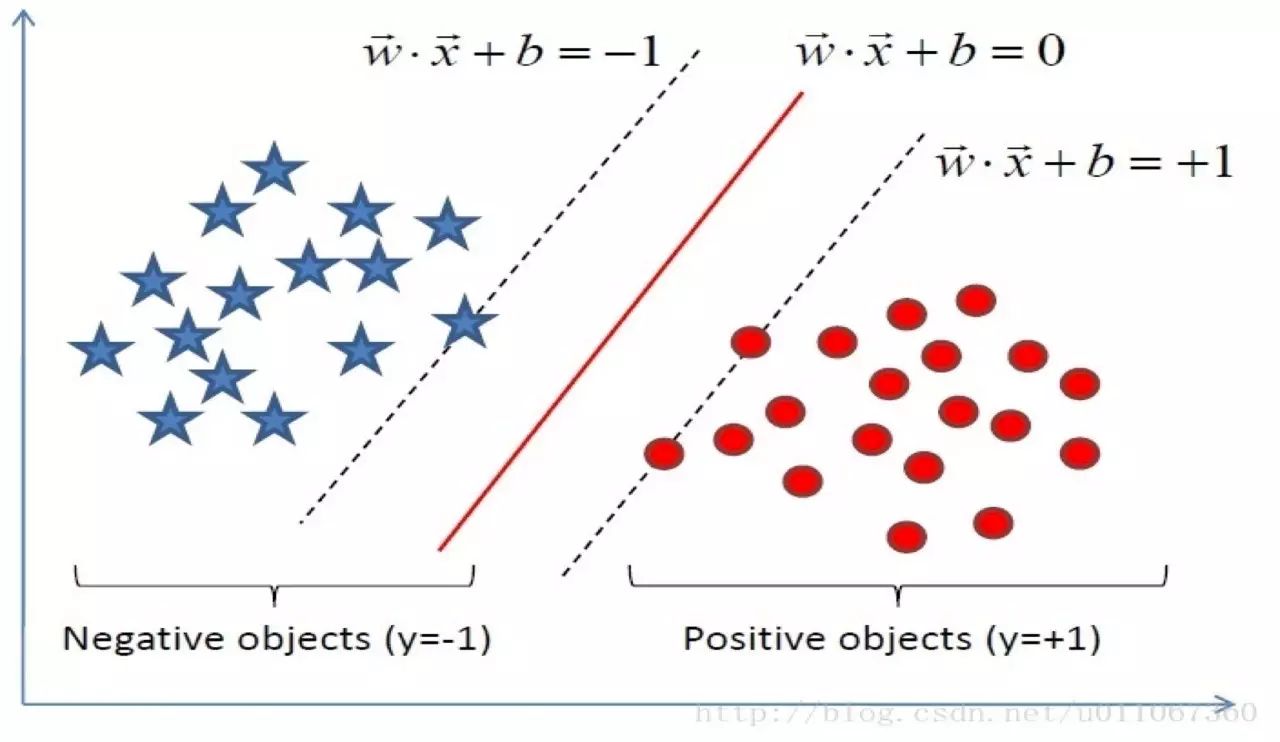
我们用 x表示离超平面最近的那些点，根据几何学的知识，我们知道点 x 到超平面的距离为：

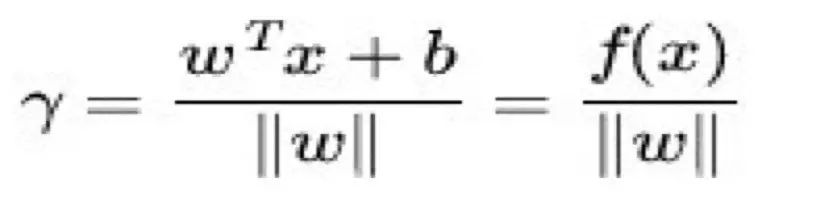
对于超平面, 表达式中的分子为1，因此支持向量到超平面的距离是1/||w||,其中||w||的意思是w的二范数。

最大化距离等价于最小化||w||, 另外由于||w||是一个单调函数，加入平方和前面的系数不影响其极值点的选取，所以原式

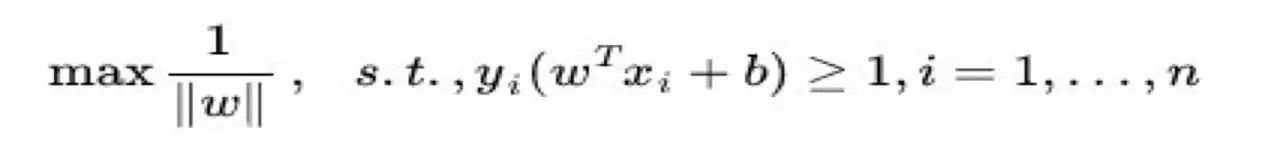
转化为：

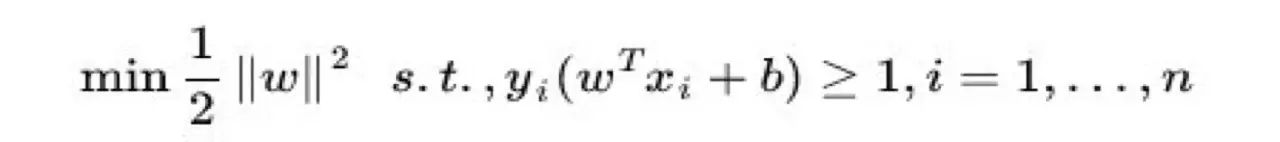
这是一个约束条件下的极值问题，可以用高数中学过的拉格朗日乘数法进行求解。

因为求解涉及到大量的数学公式和推导，现给出链接如下

https://wizardforcel.gitbooks.io/dm-algo-top10/content/svm-2.html

有兴趣的话可以详细探究求解。

2.线性不可分问题和核函数

在上文中，我们已经了解到了SVM处理线性可分的情况， 事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。比如下图左这种情况，我们称之为线性不可分。

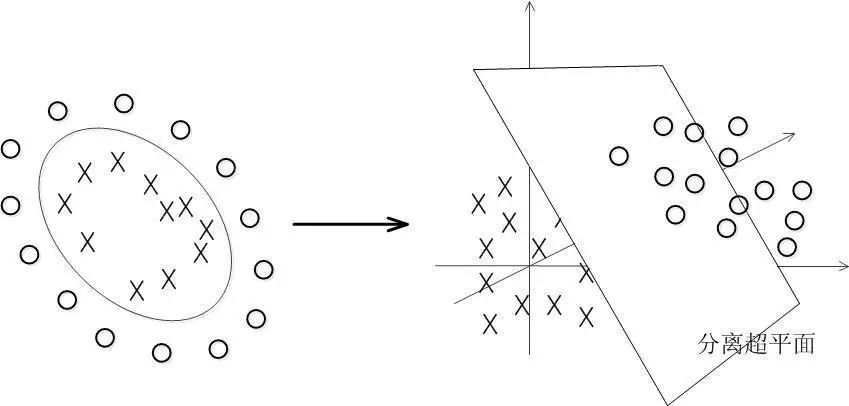
 对于非线性的情况，将数据映射到高维空间，可以解决在原始空间中线性不可分的问题，见上图右。

按此思路我们应先升维到高维空间，在高维空间中做计算求得超平面，然而高维空间虽然便利了划分，计算量也大大增加。

对于此，我们引入核函数的概念：

设X是输入空间，H为特征空间，如果存在一个从X到H的映射

φ(x)：X→H

使得所有x,z∈X，函数K（x，z）满足条件

K(x,z)=φ(x)·φ(z)

则称K(x,z)为核函数。

我们在低维空间使用核函数既利用了高维空间易分割的效果，又减少了高维空间中计算量大的缺点。下面我们一起来看看常用的核函数。

常用核函数

通常人们会从一些常用的核函数中选择（根据问题和数据的不同，选择不同的参数，实际上就是得到了不同的核函数），常用如下：

1.多项式核函数：

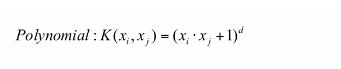
2.高斯核函数：

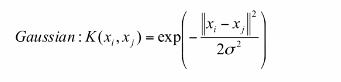
可以映射到无穷维。不过，如果选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间：

3.线性核

这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了(意思是说，咱们有的时候，写代码或写公式的时候，只要写个模板或通用表达式，然后再代入不同的核，便可以了，于此，便在形式上统一了起来，不用再分别写一个线性的，和一个非线性的)。

核函数的价值在于它虽然也是将特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上。核函数思想也被广泛应用。

参考：http://blog.csdn.net/u011067360/article/details/25322637

https://wizardforcel.gitbooks.io/dm-algo-top10/content/svm-2.html

https://zh.wikipedia.org/wiki/%E6%94%AF%E6%8C%81%E5%90%91%E9%87%8F%E6%9C%BA