支持向量机第2讲：SVM的数学原理

Posted 2021-04-26 锐翌基因

叮~~上课啦！在上期的生信课堂中，小锐带大家学习了支持向量机(SVM)的总体思想，初步了解到它可以有效地处理高通量测序数据的分类与预测问题，并介绍了它在处理线性可分问题、线性不可分问题、非线性问题时的思路（）。已get知识的童鞋请为自己鼓掌~

今天，小锐请来了特级讲师↓↓↓

是的，你没有看错，就是大数学家拉格朗日！因为今天我们要学习的是SVM的数学原理，以此帮助大家深入了解SVM算法的来源，从而可以得心应手地对模型进行参数优化，提高模型分类的正确性和回归效果。

本篇也将以线性可分样本、线性不可分样本、非线性样本的顺序来介绍。再小小地剧透下，等会儿会出现和老师同名的乘子~

注：本文中w与x都表示向量！

1

线性可分问题

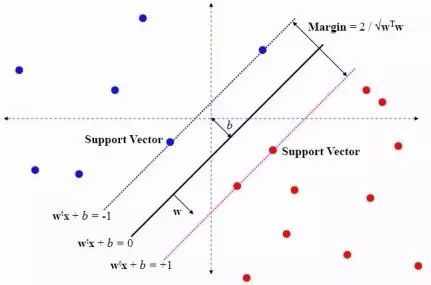
解决思路

如上图是两类线性可分的样本点。假如有两类样本点——蓝色点和红色点，蓝色点表示-1类，红色点表示+1类,寻找一个最优超平面将两类样本点最大间隔地分开。通过大量实验发现中间黑色的超平面分割效果最好。该线性超平面为wx+b=0。蓝色样本边界超平面为wx+b=-1，红色样本的边界超平面为wx+b=+1。在蓝色超平面wx+b=-1以上的点为-1类，在红色超平面wx+b=+1以下的点为+1类。即通过

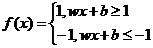
寻找超平面，尽量使模型简单。事实上，复杂的模型去拟合有限样本会导致学习机器在泛化能力（推广能力）上缺失。也就是说，线性模型的模型复杂度与边缘成反比，边缘越大，模型越简单，推广能力越强。

样本的分类模型

即将蓝色边界超平面与红色边界超平面合写，如下表示：

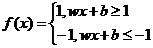
最大边缘间隔推导

假设蓝色超平面与红色超平面上分别有样本点x1、x2，则带入超平面：

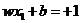
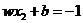
这两个超平面相减得：

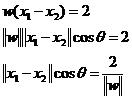
根据向量知识，两类样本点的最大边缘间隔为：

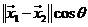
所以定义Margin为最大边缘，即

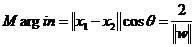
(1)

公式（1）保证模型尽量简单、推广能力强。

此时重新定义Margin’，即

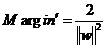
其等价于公式（1）。

定义

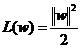
(2)

原问题是求（1）式中使间隔最大化的w，变成了求（2）式中使L(w)最小化的w。

将公式

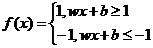
转化成

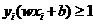
(3)

yi为因变量，即原样本标签。

式（3）保证模型对样本正确划分。

优化问题求解

这样的问题在数学上称为二次规划问题，采用“拉格朗日乘子法”来得到全局最优解。进一步地，由于约束条件为不等式，因此需要引用扩展的拉格朗日乘子理论来解决其条件极值问题。为此，定义的拉格朗日函数：

(4)

分别对公式（4）中的和求偏导，并令他们等于0：

(5)

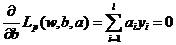
(6)

 假设w是p维，b是l维，则公式（5）有p+l+1个未知数（a是1维）。但是解（5）（6）的方程只有p+l个。又由于拉格朗日乘子是未知的，无法解出w和b。处理上面不等式约束的二次规划问题的方法是把它变成等式约束，只要限制拉格朗日乘子ai非负即可。这种变化导致的拉格朗日乘子约束就是著名的KKT条件。

引入拉格朗日乘子的公式：

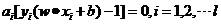
要使该等式成立，则：

因为yi只能取+1或者-1，所以，当yi=1，则wixi+b=1，表示样本为+1类；当yi=-1，则wixi+b=-1，表示样本为-1类。

由此可知，在所有的样本点中，大部分的样本点对应的拉格朗日乘子为0，只有极少数样本点（位于蓝色与红色边界超平面上的样本点）的拉格朗日乘子不等于0。

分别对式（4）中的w和b求偏导并令他们等于0，得出（5）、（6），将（5）、（6）带入（4），上面问题就转化成对偶优化问题：

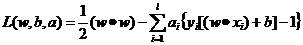
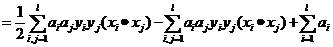
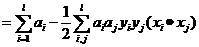
(7)

现在我们再来对比一下原始问题和对偶问题的优化思路。

原始问题：

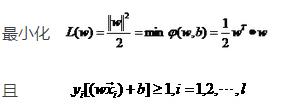
对偶问题：

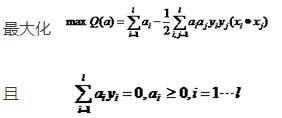
原始问题与对偶问题解的关系：

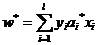
对偶优化问题可写成，求下列函数的最大值：

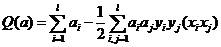
(8)

约束条件为：

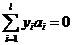
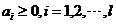
(9)

该对偶问题是关于拉格朗日乘子的，它与原问题的优化是等价的，根据这个优化问题解出最优ai（由KKT条件可知，多数为0，只有极个别非0）。

若a_i^*为最优解，则最优的w^*：

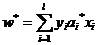
(10)

即最优分类面的系数向量是训练样本向量的线性组合。

那些非0的对应的样本才是最优分类面的参数的关键点，他们称作支持向量。

求出w后，b的求解可带入支持向量所落在的两个超平面wx+b=±1上。

求解上述问题后，得到的最优分类函数：

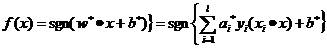
(11)

SVM的解的表达式可以重写为：

→

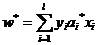
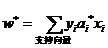
最优超平面对应的w是支持向量的线性组合。

支持向量机的判别函数为：

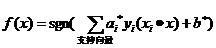
(12)

2

线性不可分问题

支持向量机最初的出发点是从线性数据开始的，但是实际中有很多数据是线性不可分的，如下图所示。这种情况下要想找超平面，就需要有一定的约束条件。  

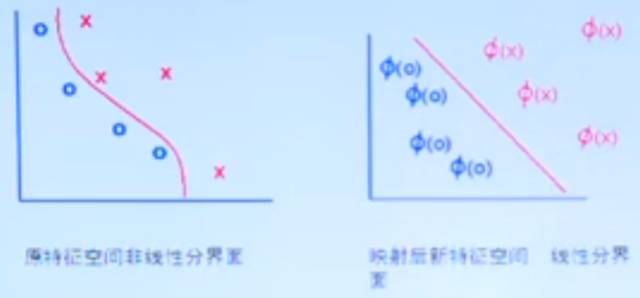
对于实际中有些线性不可分的情况，我们允许他们产生一定的错分，之前所有观测点必须位于超平面两侧，现在对于有些点给它一个宽松的条件，允许它不大于1，那么yi[(w·xi)+b]大于1的减去一个正数，这个正数即为松弛变量。

于是约束条件（2）变为：

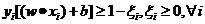
(13)

有了松弛变量的定义后，我们可以通过要求松弛变量或松弛变量的总和为最小的方式，实现对错分类数量的控制。

C是模型参数即惩罚因子，它的取值不能过大，也不能过小。它表示对松弛变量的惩罚程度，是后期SVM模型优化的参数之一。最优分类面问题就可以写成：

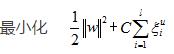
(14)

其中u=1, 2。此时仍然为二次规划问题。约束条件为：

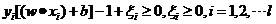
(15)

不允许有错分样本存在的情况叫做最优分类超平面的硬间隔，允许有错分样本存在的情况叫做最优分类超平面的软间隔。类似地，通过拉格朗日函数，转化为对偶问题：

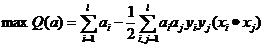
此时，我们的样本点有三类样本。

1类样本：位于分类间隔之外

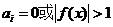
2类样本：支持向量

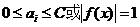
3类样本：位于分类间隔之内（允许错分的样本）

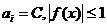
3

非线性问题

实际中有些问题即使允许错分也不能将其区分开来，即怎么样错分都不能用线性划分，需要映射到高维空间中实现划分。如下图：

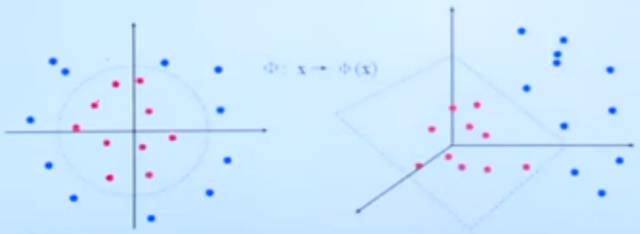
对于非线性问题，可以通过非线性变换，转化为某个高维特征空间中的线性问题，在变换空间求最优分类面，但这种变换可能比较复杂，一般情况不能实现。

值得注意的是，在前面的对偶问题，不论是寻优目标函数（8）还是分类函数（12）都只涉及到训练样本之间的内积（x·x）运算。由此设想我们如果将原特征向量用映射的方式转换成xi→Φ(xi)，则相应的式子中的x·x项只需要改成Φ(x)·Φ(x)，于是非线性问题可以转化成线性问题去解决。

设有非线性映射Φ: R→H，将输入空间R的样本映射到高维（也可能是无穷维）的特征空间H中。在特征空间H构造最优超平面时，训练算法仅用特征空间中内积，即Φ(x1)·Φ(x2)，而没有单独的Φ(x)出现。因此，如果能够找到一个函数K使得K(xi，xj)=Φ(xi)·Φ(xj)。这样，在高维特征空间实际上只需要进行内积运算，而这种内积运算可以输入空间中函数实现，我们甚至没有必要知道Φ的形式，根据泛函的有关理论，只要一种核函数满足Mercer条件，它就对应某一变换空间的内积。

Mercer条件：对于任意的对称函数K(xi, xj)能以正的系数ak>0展开成：

即用K(xi, xj)描述一个特征空间中的一个内积的充分必要条件是使得

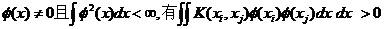
成立。这一条件并不难满足。

因此，在最优分类面中采用适当的内积K(xi, xj)就可以实现某一非线性变换后的线性分类，而计算复杂度却没有增加，此时对偶问题可以写成：

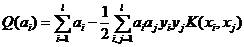
约束条件为：

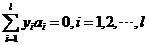
而相应的分类函数也变为：

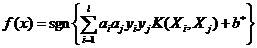
四个核函数如下：

(1)

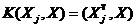
(2) 多项式核函数：

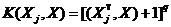
q是参数。

(3) 径向基核函数（RBF）：

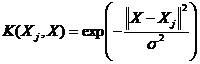
σ是参数。

(4) 双曲正切核函数：

β与γ是参数。

最后，小锐必须要再和大家叨叨一下数学原理在生信分析中的重要性。在SVM模型中，参数（惩罚因子C与核函数中的一些参数）的优化、选取对模型分类的正确性以及回归有着至关重要的作用。要想成为一名所向披靡的生信达人，必须要掌握好具体的SVM算法数学原理来对参数进行优化。大家若在学习过程中遇到困难，记得留言告诉小锐，我们的生信高手会定将帮你顺利解决！

预告：在下期的生信课堂中，我们将具体介绍SVM算法在二分类问题上的应用。当然，其在基因数据的分类应用将是重点内容，敬请期待！

供稿：范芳芳

编辑：王丽燕