支持向量机(SVM)----超详细原理分析讲解

Posted Gaolw1102

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了支持向量机(SVM)----超详细原理分析讲解相关的知识，希望对你有一定的参考价值。

文章目录

支持向量机(SVM)

支持向量机(Support Vector Machine)，是机器学习中最流行、最强大的算法模型，没有之一。

但是其背后的模型思想、数学原理较为晦涩难懂，所以本篇文章尽量使用通俗的语言讲解支持向量机的运行原理与数学推导。

直观的本质理解

我们都知道，支持向量机(SVM)大部分的应用场景均为分类问题，即如何有效地分开两种不同的类别。

首先，我们来分析下图，其中绿色、黄色分别为不同类别的数据点，如何画一条直线能够分开这两类数据呢? 假如再添加新的数据点，该直线是否还可以正确地划分呢?

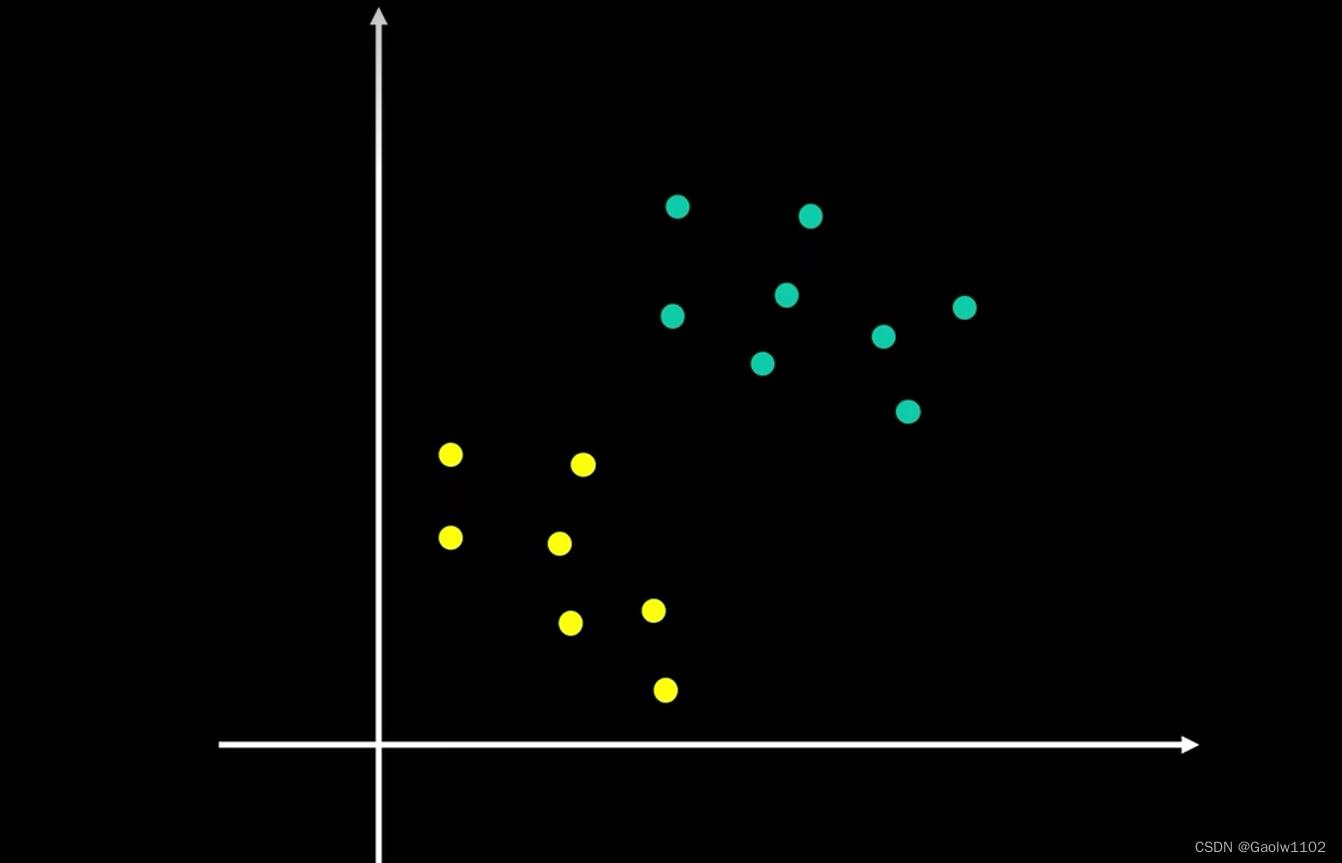
可以有以下的三种画法,都可以正确区分这两类数据点，当有新数据继续加入时，我们该选择哪种画法呢?

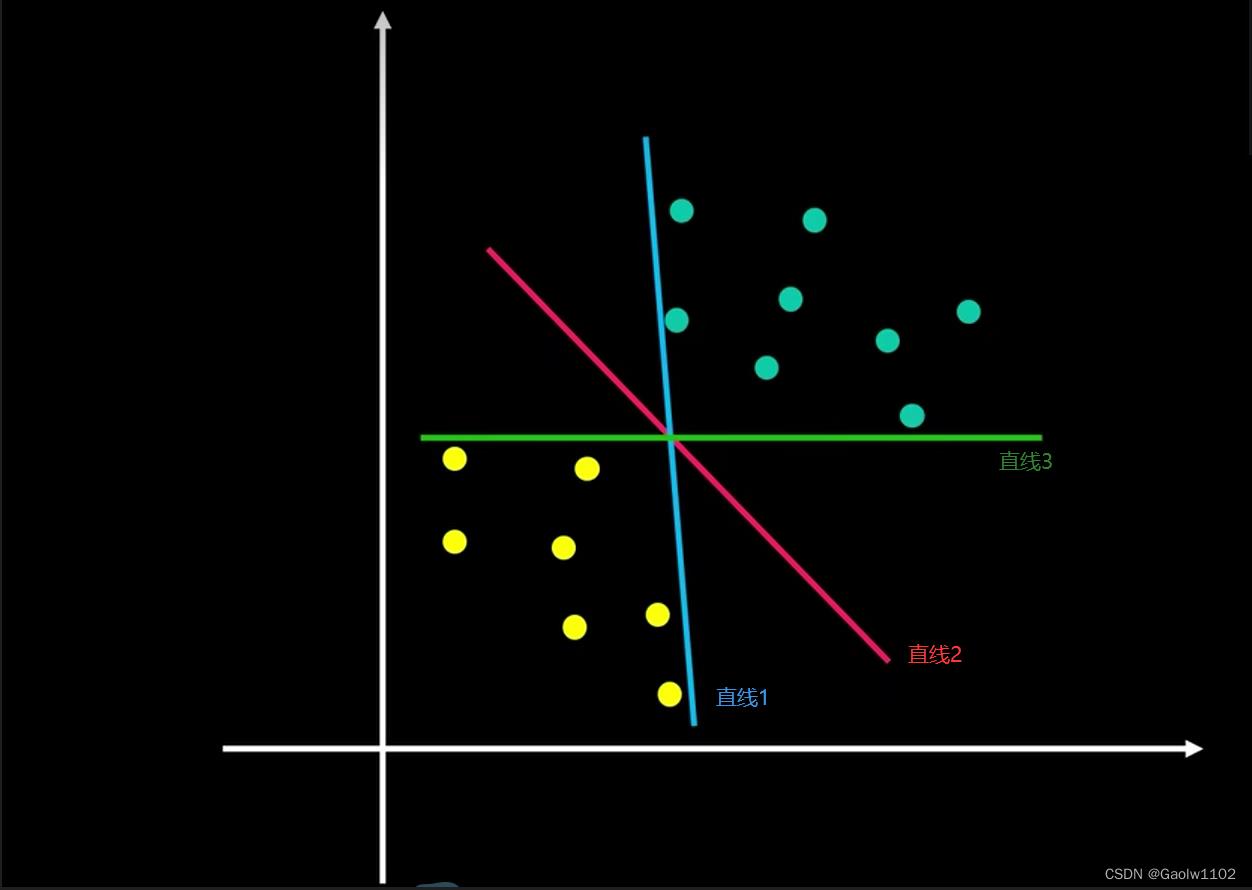
假如我们选择直线1区分两种类别数据，可能会出现以下这种情况:

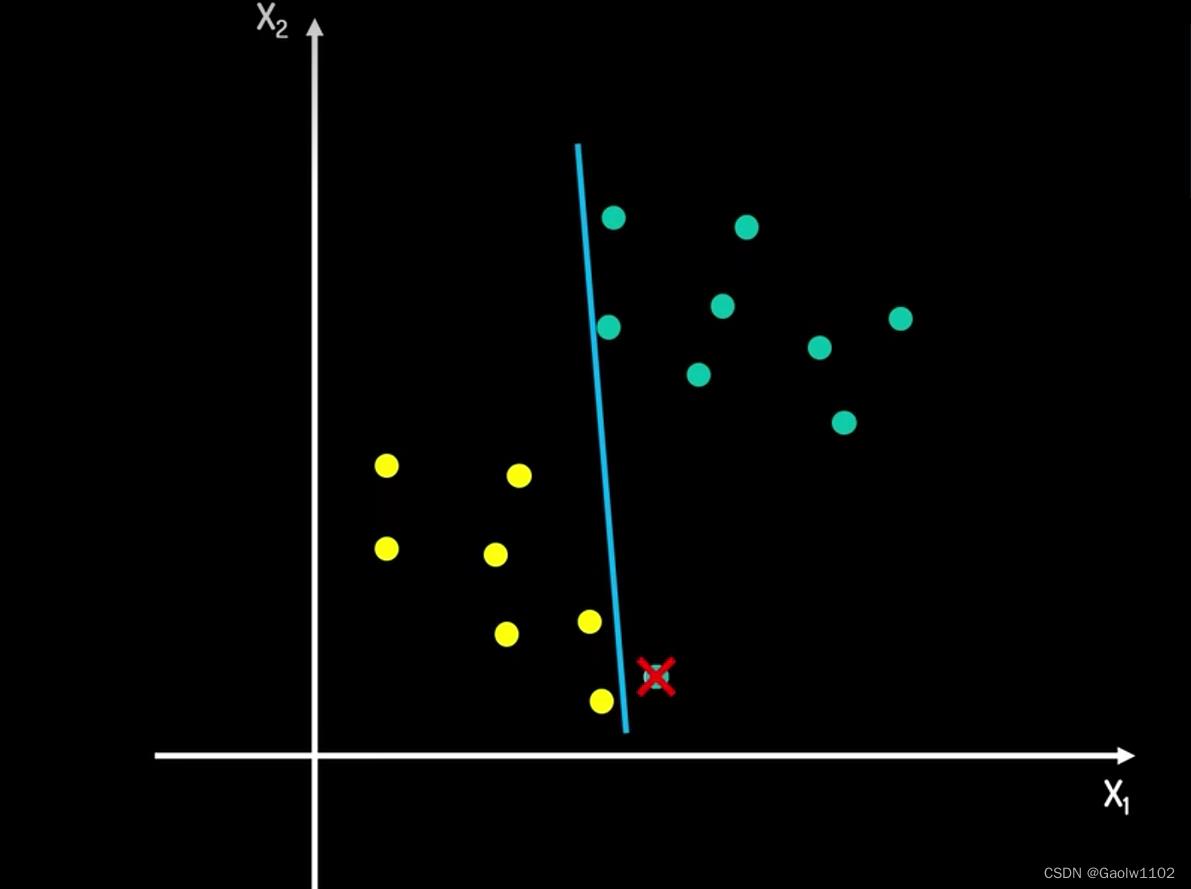
其中新添加的点的真实类别为黄色,但是根据直线1的划分方式预测新添加点类别为绿色，这样就会造成预测错误，所以以直线1的方式切分是不合理的。

同理，采用直线3的划分方式也是不科学的。故我们选用直线2的划分方式。

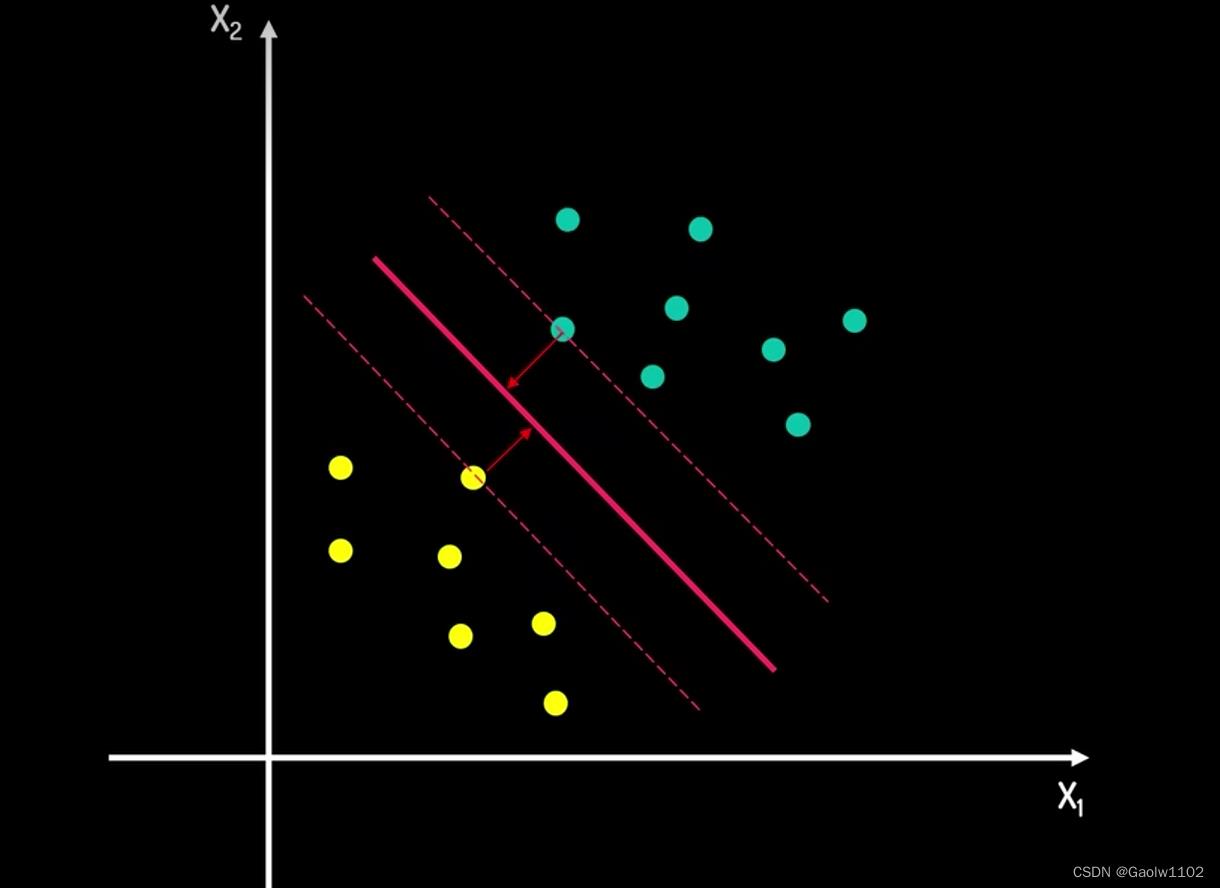
这类问题也可以推广到3维空间，甚至是高维空间, 如下图3维空间中我们采用以下划分方式

这类问题的本质就是在一个n维的数据样本中，我们该如何设计一个最优化的n-1维超平面( W 1 X 1 + W 2 X 2 + . . . + W n X n + B = 0 W_1X_1 + W_2X_2 + ... + W_nX_n + B = 0 W1​X1​+W2​X2​+...+Wn​Xn​+B=0)去划分不同类别的数据。

之后预测样本数据时，通过符号函数 s i g n ( W 1 X 1 + W 2 X 2 + . . . + W n X n + B ) sign(W_1X_1 + W_2X_2 + ... + W_nX_n + B) sign(W1​X1​+W2​X2​+...+Wn​Xn​+B)对样本数据进行分类。

几个基础概念

首先来说明一些概念，这样可能更有利于逐渐理解模型的工作原理。

决策超平面

决策超平面(Decision Hyperplane)，如上图，就是用来区分不同类别数据的超平面(在2维数据中即为直线)。

正超平面

满足( W 1 X 1 + W 2 X 2 + . . . + W n X n + B > = 1 W_1X_1 + W_2X_2 + ... + W_nX_n + B >= 1 W1​X1​+W2​X2​+...+Wn​Xn​+B>=1)所有点位于正超平面， 在该超平面内的数据点所属类别均为一个类别。

负超平面

满足( W 1 X 1 + W 2 X 2 + . . . + W n X n + B < = − 1 W_1X_1 + W_2X_2 + ... + W_nX_n + B <= -1 W1​X1​+W2​X2​+...+Wn​Xn​+B<=−1)所有点位于负超平面， 在该超平面内的数据点所属类别均为另一类别。

决策边界

在具有两个类的统计分类问题中，决策边界(Decision Boundary)或决策表面是超曲面，其将基础向量空间划分为两个集合，一个集合。 分类器(SVM) 将决策边界一侧的所有点分类为属于一个类，而将另一侧的所有点分类为属于另一个类。(百度百科)

支持向量

支持向量(Support Vector)是位于决策边界上的样本数据点，决定间隔距离，其距离超平面最近。

在支持向量机中，距离超平面最近的且满足一定条件的几个训练样本点被称为支持向量。

硬间隔

硬间隔(Hard Margin)，即两个决策边界之间的距离，本质上求解的最优超平面就是寻找一个具备 最大硬间隔(Max Hard Margin) 的问题。

硬间隔不允许出现异常的点，即不允许出现落在决策边界与决策超平面之内的点，通常来讲这种情况是理想状态下的，与之相对的是软间隔。

软间隔

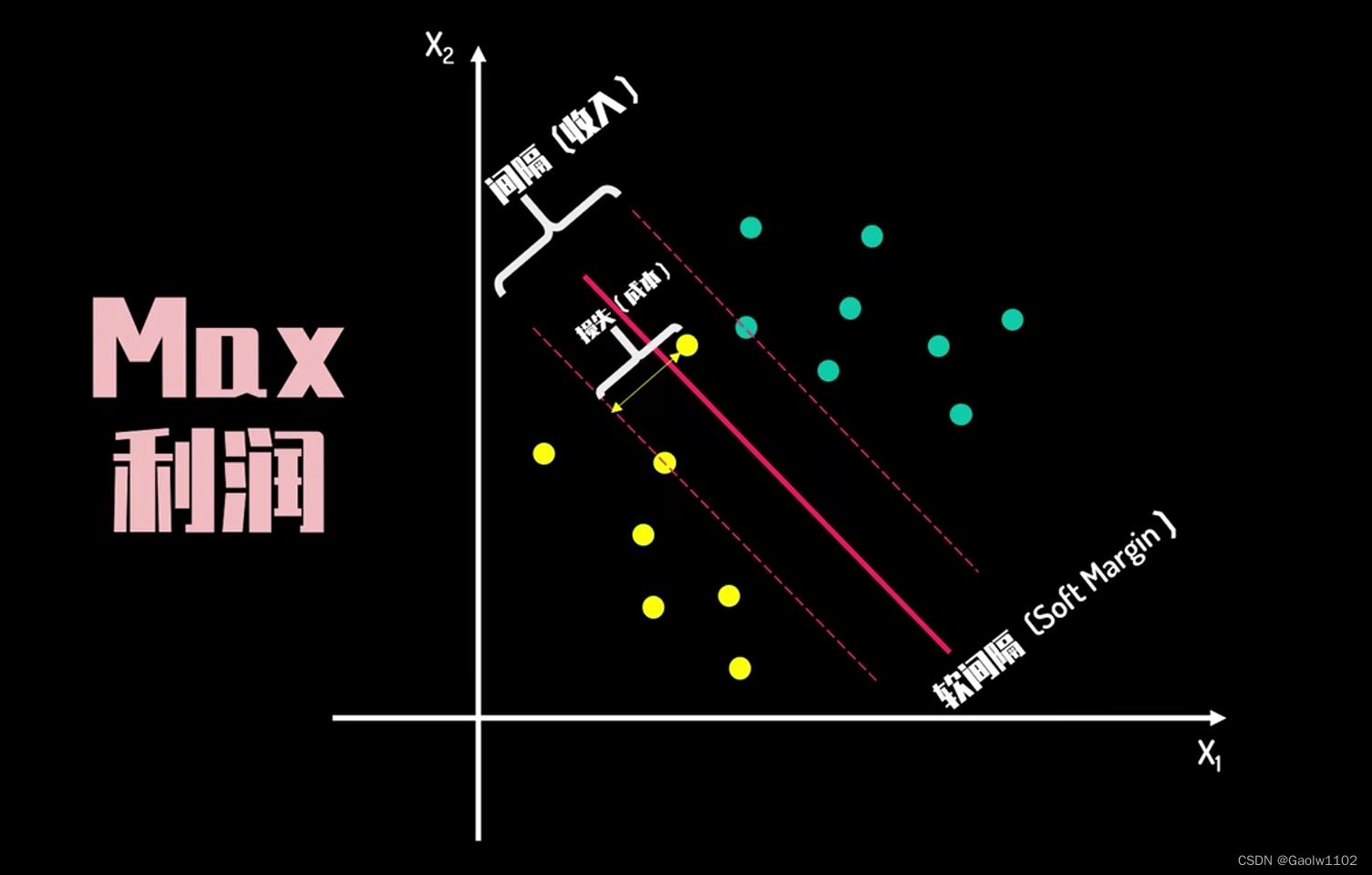
软间隔(Soft Margin)，具备一定的容错率，能够允许数据样本中异常值的出现，它试图在间隔距离和错误大小之间寻找一个平衡。

可以把硬间隔想象为收入，异常数据(损失loss)想象为成本，那么软间隔就为 收入 - 成本 = 利润，它试图寻找最大利润值，即最大软间隔(Max Soft Margin)。

决策超平面的求解(SVM模型的推导)

由以上可知，SVM的核心问题就是寻找最优超平面问题，也即寻找决策边界的最大间隔问题。

求解 硬间隔(Hard Margin) 下的决策超平面(软间隔类似)后，决策超平面( W 1 X 1 + W 2 X 2 + . . . + W n X n + B = 0 W_1X_1 + W_2X_2 + ... + W_nX_n + B = 0 W1​X1​+W2​X2​+...+Wn​Xn​+B=0)便可以利用符号函数对样本进行预测分类。

最大硬间隔的寻找与公式构建

首先，我们先选取两个支持向量 x n , x m x_n, x_m xn​,xm​，分别代表两个不同的类别，如下图

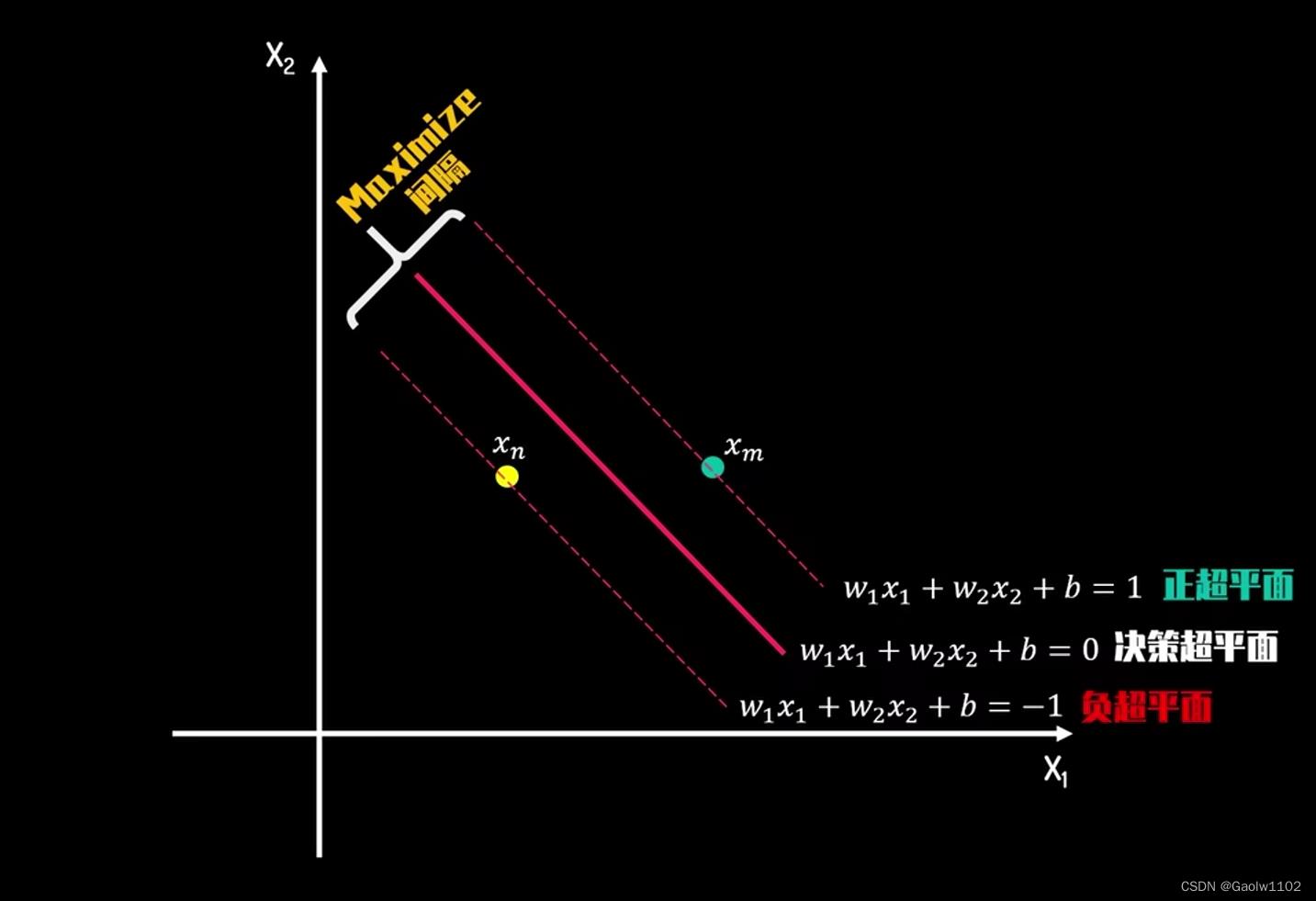
因为该两点均在决策边界上，故必定满足以下方程式

w 1 x 1 m + w 2 x 2 m + b = 1 ( 1 ) w 1 x 1 n + w 2 x 2 n + b = − 1 ( 2 ) \\begincases w_1x_1m + w_2x_2m + b = 1\\qquad\\qquad\\qquad\\left (1)\\right.\\\\ w_1x_1n + w_2x_2n + b = -1\\qquad\\qquad\\qquad\\left (2)\\right. \\endcases w1​x1m​+w2​x2m​+b=1(1)w1​x1n​+w2​x2n​+b=−1(2)​

将等式(1) - 等式(2)，可得等式(3)如下

w 1 x 1 m − w 1 x 1 n + w 2 x 2 m − w 2 x 2 n = 2 w_1x_1m - w_1x_1n + w_2x_2m - w_2x_2n = 2 w1​x1m​−w1​x1n​+w2​x2m​−w2​x2n​=2

( w 1 x 1 m + w 2 x 2 m ) − ( w 1 x 1 n + w 2 x 2 n ) = 2 (w_1x_1m + w_2x_2m) -(w_1x_1n + w_2x_2n) = 2 (w1​x1m​+w2​x2m​)−(w1​x1n

以上是关于支持向量机(SVM)----超详细原理分析讲解的主要内容，如果未能解决你的问题，请参考以下文章

支持向量机（SVM）的详细推导过程及注解

机器学习--支持向量机 （SVM）算法的原理及优缺点

9幅图快速理解支持向量机（SVM）的工作原理

九张图快速理解支持向量机（SVM）的工作原理

SVM-支持向量机原理详解与实践之一

SVM -支持向量机原理详解与实践之二