主成分析与支持向量机的数字识别模型

Posted 2021-04-26 自科部

基于主成分析与支持向量机的数字识别模型

题目要求: 输入图片,识别数字

简单的分类问题

载入数据

• 载入常用库

 import os
import pandas as pd
import os, random
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import ticker
from sklearn import linear_model, svm, preprocessing, decomposition, model_selection
import seaborn as sns
%matplotlib inline 

先来看下我们的训练数据

DATAPATH="D:/dataset/Digit/"
print(os.listdir(DATAPATH))
train_file=DATAPATH+"train.csv"
train = pd.read_csv(train_file)
print(train.shape)
train

['sample_submission.csv', 'test.csv', 'train.csv'](42000, 785)

label	pixel0	pixel1	pixel2	pixel3	pixel4	pixel5	pixel6	pixel7	pixel8	...	pixel774	pixel775	pixel776	pixel777	pixel778	pixel779	pixel780	pixel781	pixel782	pixel783
0	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
3	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
6	7	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
7	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
8	5	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
9	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
10	8	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
11	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
12	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
13	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
14	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
15	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
16	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
17	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
18	7	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
19	5	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
20	8	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
21	6	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
22	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
23	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
24	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
25	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
26	6	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
27	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
28	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
29	7	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
41970	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41971	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41972	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41973	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41974	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41975	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41976	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41977	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41978	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41979	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41980	7	0	0	0	0	0	0	0	0	0	...	27	253	110	0	0	0	0	0	0	0
41981	2	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41982	8	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41983	7	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41984	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41985	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41986	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41987	5	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41988	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41989	5	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41990	3	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41991	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41992	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41993	6	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41994	4	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41995	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41996	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41997	7	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41998	6	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
41999	9	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

42000 rows × 785 columns

可以看到我们的数据是一个42000 * 785 大小的矩阵, 每一行代表一组训练数据,第一列是所对应的数字,接下来784(28*28)列是对应各个像素点的灰度值(0-255).

随便看一下几张图片

j=0
for i in [0,1,2,124,1234,42,233,8888,9999]:
    j+=1
    plt.subplot(3, 3, j)
    plt.imshow( np.array(train.iloc()[i].values[1:]).reshape((28,28))/255.0)
plt.show()

数据预处理

• 提取标签

Y = train.loc[:,'label':'label'].values.flatten()
Y[0:20]

array([1, 0, 1, 4, 0, 0, 7, 3, 5, 3, 8, 9, 1, 3, 3, 1, 2, 0, 7, 5],dtype=int64)

• 归一正则化

X = preprocessing.normalize(train.loc[:,'pixel0':].values)

• 按8:2的比例分割数据集

(X, X_test, y, y_test) = model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)

搭建模型

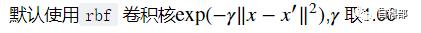
est = svm.SVC(C=1.61, gamma=1.66,cache_size=4096)

训练模型

TRAINCOUNT=10000 ##### 训练用数据,现在测试的话小一点,真正训练就等于训练集大小
#TRAINCOUNT=train.shape[0]
est.fit(X[:TRAINCOUNT], y[:TRAINCOUNT])

验证模型

 

est.score(X_test, y_test)

0.9698809523809524

测试集

test_file=DATAPATH+"test.csv"
test = pd.read_csv(test_file)
T=preprocessing.normalize(test.loc[:,'pixel0':].values)

预测测试集

ans = est.predict(T)
ans

array([2, 0, 9, ..., 3, 9, 2], dtype=int64)

处理与写入文件

ids = np.reshape(np.arange(1, ans.shape[0] + 1), (-1, 1))
answer_column = np.reshape(ans, (-1, 1))
answer_matrix = np.append(ids, answer_column, axis=1)
df = pd.DataFrame(answer_matrix, columns=["ImageId", "Label"])
df.to_csv("simplesvm.csv", sep=",", index=False)

在排行榜上取得 0.96714 的成绩

优化在优化之前先找出上面代码的问题,

首先,我们只用到了前1w个数据来进行训练,这是为了加快训练速度,你可以用全部的训练数据进行训练(包括训练集与验证集),模型的最终效果可能会好一点.不过注意一点,官方的说法是svm算法的时间复杂度

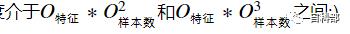
其次,在定义svm模型时使用了两个魔数1.61和1.68,或许改变这两个数字会改善模型的性能?主成分分析要加快训练速度,从特征数下手,我们使用PCA的前50个数据当作新的特征数据(即从784降到50).

• 进行主成分分析

pca = decomposition.PCA(n_components=50, whiten=True)
X=preprocessing.normalize(train.loc[:,'pixel0':].values)
X=pca.fit(X).transform(X)

pd.DataFrame(X[:3])#显示主成分析后结果

	0	1	2	3	4	5	6	7	8	9	...	40	41	42	43	44	45	46	47	48	49
0	1.535293	-1.110612	-0.731363	1.333155	-1.754703	-1.092480	1.812278	0.289279	1.612573	-0.288227	...	0.124678	-0.428828	0.589311	1.479232	-0.111943	-1.297064	0.085061	-0.773294	0.459028	0.505223
1	-1.483209	-1.734452	0.313483	0.104703	-0.864101	2.068636	-1.027981	-0.446621	0.151356	-0.484600	...	0.626253	-0.272523	0.466507	0.736921	-0.383676	-0.277259	0.269298	-1.149686	0.696214	-0.027801
2	2.021091	0.318131	0.452610	-1.208539	1.750276	1.823014	-0.857398	-0.999567	0.806976	1.349876	...	0.726378	-0.461264	0.931743	-1.264687	1.398559	0.577552	-0.054154	-0.248361	-0.167295	-0.761548

3 rows × 50 columns

• 重新分割数据集 8:2

 (X, X_test, y, y_test) = model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)

• 再训练与验证一次

est = svm.SVC(C=1.61, gamma=1.66,cache_size=4096)
est.fit(X[:TRAINCOUNT], y[:TRAINCOUNT])
est.score(X_test, y_test)

0.1144047619047619

可以看到效果不是很好,但是我们把 和C 改成0.00774和4.17531的话

est = svm.SVC(C=4.17531, gamma=0.00774,cache_size=4096)
est.fit(X[:TRAINCOUNT], y[:TRAINCOUNT])
est.score(X_test, y_test)

0.9657142857142857

可以看到参数的选择对性能影响很大,那么怎么找到比较好的参数呢?

答案是:一个一个找

首先定义查找的范围

C_range = np.logspace(-6, 6, 30)
gamma_range = np.logspace(-6, 1, 10)
C_range,gamma_range

(array([1.00000000e-06, 2.59294380e-06, 6.72335754e-06, 1.74332882e-05,.52035366e-05, 1.17210230e-04, 3.03919538e-04, 7.88046282e-04,.04335972e-03, 5.29831691e-03, 1.37382380e-02, 3.56224789e-02,.23670857e-02, 2.39502662e-01, 6.21016942e-01, 1.61026203e+00,.17531894e+00, 1.08263673e+01, 2.80721620e+01, 7.27895384e+01,.1.88739182e+02, 4.89390092e+02, 1.26896100e+03, 3.29034456e+03,.8.53167852e+03, 2.21221629e+04, 5.73615251e+04, 1.48735211e+05,.85662042e+05, 1.00000000e+06]),rray([1.00000000e-06, 5.99484250e-06, 3.59381366e-05, 2.15443469e-04,.29154967e-03, 7.74263683e-03, 4.64158883e-02, 2.78255940e-01,.66810054e+00, 1.00000000e+01]))

定义待查找参数的模型

svc = svm.SVC(kernel="rbf",cache_size=4096)

查找器,

它将会把C_range和gamma_range进行组合,当作模型的参数,对每个模型用训练数据训练,验证数据验证,找出验证结果最好的参数组合

clf = model_selection.GridSearchCV(estimator=svc, cv=model_selection.ShuffleSplit(n_splits=1, test_size=0.2, random_state=0)
                                   , param_grid=dict(C=C_range, gamma=gamma_range), n_jobs=-1,verbose=1)

下面的代码一共训练了30*10 个模型,所以数据量不要太大

 

SEARCHMAX=1000
clf.fit(X[:SEARCHMAX], y[:SEARCHMAX])

我们看下结果

import matplotlib.cm as cm
from matplotlib.colors import Normalize
plt.imshow(clf.cv_results_["mean_test_score"].reshape(30,10), 
        cmap=cm.hot,norm=Normalize())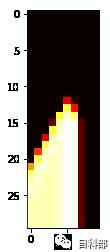

横坐标表示gamma参数,纵坐标表示C参数,左上角是最小的两个参数的组合

我们来看下最好的参数组合长怎么样

clf.best_params_

{'C': 4.175318936560401, 'gamma': 0.007742636826811269}

也就是上面用的数字:)我们可以进行二次查找,不过要确定新的数据范围

先看下在gamma=0.007742636826811269时,验证的准确率随C的表现,和C=4.175318936560401时gamma的表现

plt.plot(clf.cv_results_["mean_test_score"].reshape(30,10)[:,5])
plt.show()
plt.plot(clf.cv_results_["mean_test_score"].reshape(30,10)[16,:])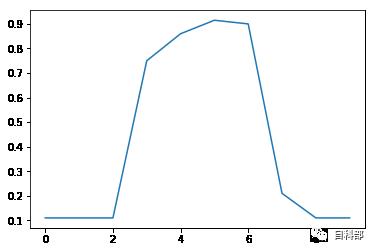

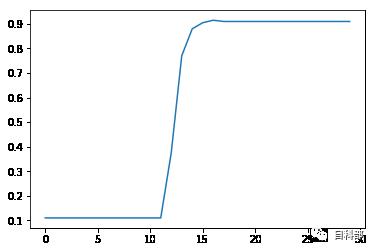
可以看到在C[12]之后准确率开始增长,且图像程tanh形状的,我们下次就从C[12]开始,使用线性范围.对于gamma,可以看到波峰在第4到第8中间,我们继续选用log.

新的参数列表如下

C_range2 = np.linspace(C_range[12], C_range[17], 20, endpoint=True)
gamma_range2 = np.logspace(np.log(gamma_range[5]), np.log(gamma_range[8]), 20)
(C_range2 ,gamma_range2)

(array([ 0.09236709,  0.65731447,  1.22226185,  1.78720923,  2.35215661,.91710399,  3.48205138,  4.04699876,  4.61194614,  5.17689352,.7418409 ,  6.30678828,  6.87173567,  7.43668305,  8.00163043,.56657781,  9.13152519,  9.69647258, 10.26141996, 10.82636734]),rray([1.37716833e-05, 2.64095277e-05, 5.06447279e-05, 9.71198157e-05,.86243643e-04, 3.57153627e-04, 6.84902377e-04, 1.31341594e-03,.51869679e-03, 4.83002632e-03, 9.26239089e-03, 1.77621982e-02,.40620138e-02, 6.53196620e-02, 1.25261479e-01, 2.40210034e-01,.60643293e-01, 8.83361283e-01, 1.69399439e+00, 3.24852023e+00]))

再次训练

svc = svm.SVC(kernel="rbf",cache_size=4096)
clf = model_selection.GridSearchCV(estimator=svc, cv=model_selection.ShuffleSplit(n_splits=1, test_size=0.2, random_state=0)
                                   , param_grid=dict(C=C_range2, gamma=gamma_range2), n_jobs=-1,verbose=1)
SEARCHMAX=1000
clf.fit(X[:SEARCHMAX], y[:SEARCHMAX])
plt.imshow(clf.cv_results_["mean_test_score"].reshape(20,20), 
        cmap=cm.hot,norm=Normalize())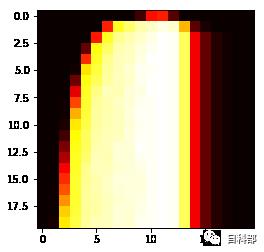

可以看到热力图基本居中,我们的参数范围还行,看下这次最好的参数列表

clf.best_params_

{'C': 1.222261849194718, 'gamma': 0.01776219824452757}

两个数字比起前一次有大的改变,不过C对性能影响不是很大,gamma是指数分布的,换成对数的话差别小,

用新的参数训练模型,再验证

 

est = svm.SVC(C=1.7872092309327074, gamma=0.01776219824452757,cache_size=4096)
est.fit(X[:TRAINCOUNT], y[:TRAINCOUNT])
est.score(X_test, y_test)

0.9696428571428571

提高了0.4%,emmmmmmm

上面用1000个数据匹配参数的,花了50多秒,现在我们用不同数量进行测试

 

svc = svm.SVC(kernel="rbf",cache_size=4096)
clf = model_selection.GridSearchCV(estimator=svc, cv=model_selection.ShuffleSplit(n_splits=1, test_size=0.2, random_state=0)
                                   , param_grid=dict(C=C_range2, gamma=gamma_range2), n_jobs=-1,verbose=1)
SEARCHMAX=2000
clf.fit(X[:SEARCHMAX], y[:SEARCHMAX])
plt.imshow(clf.cv_results_["mean_test_score"].reshape(20,20), 
        cmap=cm.hot,norm=Normalize())
clf.best_params_

{'C': 4.611946139622656, 'gamma': 0.009262390888788635}

发现最优参数变了

再训练一次,然后提交看看

 

est = svm.SVC(C=4.0469987578846665, gamma=0.009262390888788635,cache_size=4096,verbose=True)
est.fit(X, y)
est.score(X_test, y_test)

0.9788095238095238

我们这次载入测试数据时要注意与训练数据进行同种预处理,不然预测的结果就不对了

test_file=DATAPATH+"test.csv"
test = pd.read_csv(test_file)
T=preprocessing.normalize(test.values)
T=pca.transform(T)
ans=est.predict(T)
ans

array([2, 0, 9, ..., 3, 9, 2], dtype=int64)

ids = np.reshape(np.arange(1, ans.shape[0] + 1), (-1, 1))
answer_column = np.reshape(ans, (-1, 1))
answer_matrix = np.append(ids, answer_column, axis=1)
df = pd.DataFrame(answer_matrix, columns=["ImageId", "Label"])
df.to_csv("pcasvm.csv", sep=",", index=False)

LB分数0.97914