006：支持向量机

Posted 2021-04-26 奇异果说AI

支持向量机

“支持向量机”（SVM）是一种有监督的机器学习算法，可用于分类任务或回归任务。但是，它主要适用于分类问题。在我第一次听到“支持向量机”这个名字，我觉得这个名字听起来好复杂，如果连名字都这么复杂的话，那么这个名字的概念将超出我的理解。

No1. 如何理解支持向量机

假如给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点，用y表示类别（y可以取1或者0，分别代表两个不同的类），一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面。这个超平面可以用分类函数表示，当f(x) 等于0的时候，x便是位于超平面上的点，而f(x)大于0的点对应 y=1 的数据点，f(x)小于0的点对应y=-1的点：

对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的置信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

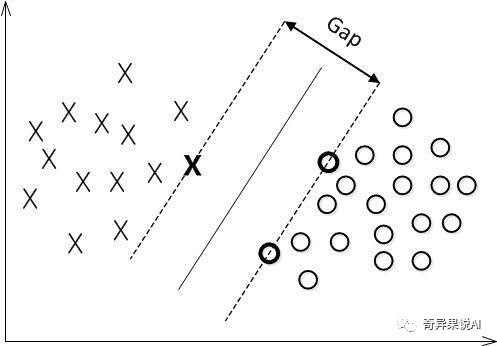
No2. 核函数

事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。在上文中，我们已经了解到了 SVM 处理线性可分的情况，那对于非线性的数据 SVM 咋处理呢？对于非线性的情况，SVM 的处理方法是选择一个核函数 kernel，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。具体来说，在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。如下图所示，一堆数据在二维空间无法划分，从而映射到三维空间里划分：

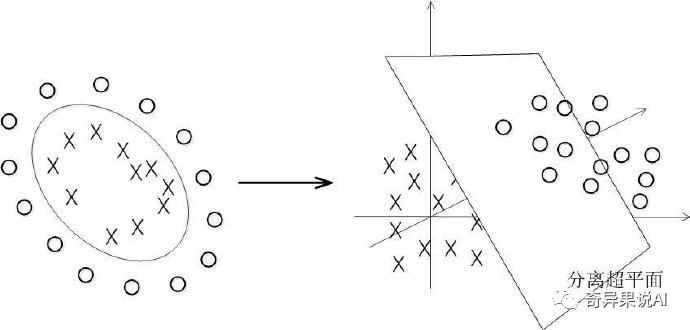
通常人们会从一些常用的核函数中选择（根据问题和数据的不同，选择不同的参数，实际上就是得到了不同的核函数），例如：多项式核、高斯核、线性核、径向基核。

也许你还是没明白核函数到底是个什么东西？我再简要概括下，即以下三点：

1. 实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去，映射到高维空间后，相关特征便被分开了，也就达到了分类的目的。

2. 但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的。那怎么办呢？

3. 此时，核函数就隆重登场了，核函数的价值在于它虽然也是将特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，避免了直接在高维空间中的复杂计算。

SVM 在应用在诸如文本分类，图像分类，手写字符识别等领域，但或许你并没强烈的意识到，SVM 可以成功应用的领域远远超出现在已经在开发应用了的领域。

No3. LR和SVM的区别和联系

相同点

• 都是线性分类器。本质上都是求一个最佳分类超平面。

• 都是监督学习算法。

• 都是判别模型。判别模型不关心数据是怎么生成的，它只关心信号之间的差别，然后用差别来简单对给定的一个信号进行分类。常见的判别模型有：KNN、SVM、LR，常见的生成模型有：朴素贝叶斯，隐马尔可夫模型。

不同点

• LR 是参数模型，SVM 是非参数模型，Linear 和 rbf 核则是针对数据线性可分和不可分的区别。

• SVM 的处理方法是只考虑 支持向量，也就是和分类最相关的少数点，去学习分类器。而 LR 通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。

• 逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而 SVM 的理解和优化相对来说复杂一些，SVM 核函数计算时优势很明显,能够大大简化模型和计算。

• LR 能做的 SVM 能做，但可能在准确率上有问题，SVM 能做的 LR 有的做不了。

  
  

import numpy as npimport sklearn.model_selection as msimport sklearn.svm as svmimport sklearn.metrics as smimport matplotlib.pyplot as mp
x, y = [],[]data=np.loadtxt('multiple2.txt',  delimiter=',')x = data[:, :-1]y = data[:, -1]# 拆分训练集与测试集train_x, test_x, train_y, test_y = \ ms.train_test_split(x, y, test_size=0.25, random_state=5)# 基于线性核函数的svm绘制分类边界（linear和rbf）model=svm.SVC(kernel='linear')model.fit(train_x, train_y)
# 绘制分类边界线l, r = x[:, 0].min()-1, x[:, 0].max()+1b, t = x[:, 1].min()-1, x[:, 1].max()+1n = 500grid_x, grid_y = np.meshgrid( np.linspace(l, r, n), np.linspace(b, t, n))# 模型的输入,预测输出mesh_x = np.column_stack( (grid_x.ravel(), grid_y.ravel()))pred_mesh_y = model.predict(mesh_x)grid_z = pred_mesh_y.reshape(grid_x.shape)
# 看一看测试集的分类报告pred_test_y = model.predict(test_x)cr = sm.classification_report( test_y, pred_test_y)print(cr)
mp.figure('SVM', facecolor='lightgray')mp.title('SVM', fontsize=16)mp.xlabel('X', fontsize=14)mp.ylabel('Y', fontsize=14)mp.tick_params(labelsize=10)mp.pcolormesh(grid_x,grid_y,grid_z,cmap='brg')mp.scatter(x[:,0], x[:,1], s=60,  c=y, label='points', cmap='jet')
mp.legend()mp.show()

测试输出结果：

 precision recall f1-score support
 0.0 0.64 0.96 0.77 45 1.0 0.75 0.20 0.32 30
 accuracy 0.65 75 macro avg 0.70 0.58 0.54 75weighted avg 0.69 0.65 0.59 75

linear 分类效果：

rbf 分类效果：

可见根据数据特点需要搭配不同的核函数。

最后，总结一下：

SVM本质上即是一个分类方法，用 w^T+b 定义分类函数，求w、b寻找最大间隔。

最近很忙，更新不易。点击"在看"，留下你的想法