机器学习套路：朴素贝叶斯

Posted 2021-04-25 算法爱好者

（点击上方公众号，可快速关注）

http://sharkdtu.com/posts/ml-nb.html

朴素贝叶斯（NaiveBayes）是基于贝叶斯定理与特征条件独立假设的一种分类方法，常用于文档分类、垃圾邮件分类等应用场景。

其基本思想是，对于给定的训练集，基于特征条件独立的假设，学习输入输出的联合概率分布，然后根据贝叶斯定理，对给定的预测数据，预测其类别为后验概率最大的类别。

基本套路

给定训练集 TT，每个实例表示为 (x,y)，其中 x 为 n 维特征向量，定义 X 为输入(特征)空间上的随机向量，Y 为输出(类别)空间上的随机变量，根据训练集计算如下概率分布：

先验概率分布，即每个类别在训练集中概率分布

 

条件概率分布，即在每个类别下，各特征的条件概率分布

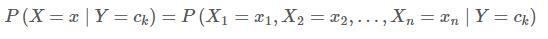
假设每个特征之间是独立的，那么上述条件概率分布可以展开为如下形式：

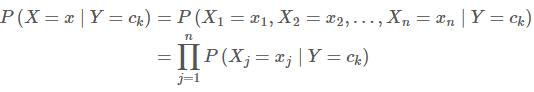
如果有了每个类别的概率 P(Y=ck)，以及 每个类别下每个特征的条件概率 P(Xj=xj∣Y=ck)，那么对于一个未知类别的实例 x，就可以用贝叶斯公式求解其属于每个类别的后验概率：

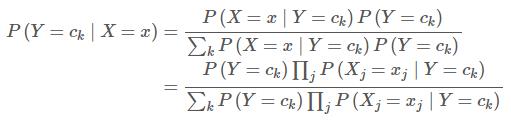
对于每个实例，分母都一样，则将该实例的类别判别为：

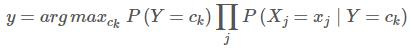
应用套路

那么如何求解 P(Y=ck)和 P(Xj=xj∣Y=ck)这些概率值呢？答案是极大似然估计。先验概率的极大似然估计为：

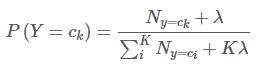
对于条件概率 P(Xj=xj∣Y=ck)的极大似然估计通常有两种模型：多项式模型和伯努利模型。

多项式模型

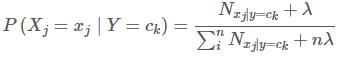
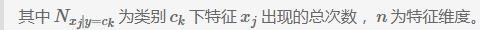
伯努利模型

对于每个特征 xj，只能有{0, 1}两种可能的取值：

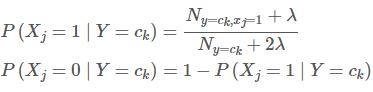
通过给定的训练集，根据上述极大似然估计方法，可以求得朴素贝叶斯模型的参数(即上述的先验概率和条件概率)，基于这些参数即可根据下面的模型对未知类别的数据进行预测。

总结

朴素贝叶斯模型是基于特征之间独立的假设，这是个非常强的假设，这也是其名字的由来，它属于生成学习方法，训练时不需要迭代拟合，模型简单易于理解，常用于文本分类等，并能取得较好的效果。

觉得本文有帮助？请分享给更多人

关注「算法爱好者」，修炼编程内功