机器学习面试题——朴素贝叶斯
Posted 冰露可乐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习面试题——朴素贝叶斯相关的知识,希望对你有一定的参考价值。
机器学习面试题——朴素贝叶斯
提示:这些知识点也是大厂笔试经常考的题目,我记得阿里和京东就考!!!想必在互联网大厂就会用这些知识解决实际问题
朴素贝叶斯介绍一下
朴素贝叶斯优缺点
贝叶斯公式
朴素贝叶斯中的“朴素”怎么理解?
什么是拉普拉斯平滑法?
朴素贝叶斯中有没有超参数可以调?
你知道朴素贝叶斯有哪些应用吗?
朴素贝叶斯对异常值敏不敏感?
频率学派与贝叶斯学派的差别
概率与期望的公式
先验概率与后验概率
文章目录
朴素贝叶斯介绍一下
朴素贝叶斯是一个基于特征条件独立假设和贝叶斯原理的一种分类算法。
朴素贝叶斯通过训练数据得到X与y的联合分布;
之后对于要预测的X,根据贝叶斯公式,输出后验概率最大的y。
朴素贝叶斯是一种生成式学习算法,其生成方法通过学习X,Y的联合分布来实现的。
假设各个特征在给定y的情况下是相互独立的。

朴素贝叶斯分类:贝叶斯公式:
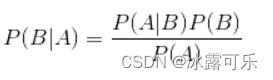
换个表达形式就会明朗很多,如下:
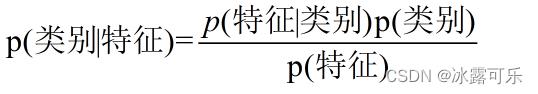
我们最终求的p(类别|特征) 即可!就是给定物品的特征,请你为其制定分类类别。
就相当于完成了我们的分类任务。
不妨设:我们想让p(B、C、D、E|A) = p(B|A)*p(C|A)*p(D|A)*p(E|A),
那么我就要分别统计后面几个概率,也就得到了左边的概率!
朴素贝叶斯分类有朴素一词的来源,即假设各个特征之间相互独立,那么这个等式就成立了!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
朴素贝叶斯优缺点
优点:
(1)算法逻辑简单,易于实现
(2)分类过程中时空开销小,分类准确度高,速度快。
(3)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
(4)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
(5)对小规模的数据表现很好,能处理多分类任务,适合增量式训练
缺点:
(1)理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
(2)需要知道先验概率,且先验概率很多时候是基于假设或者已有的训练数据所得的,这在某些时候可能会因为假设先验概率的原因出现分类决策上的错误。
贝叶斯公式

公式中,事件B的概率为P(B),
事件B已发生条件下事件A的概率为P(A│B),
事件A发生条件下事件B的概率为P(B│A)。
举个简单的例子:
村子有且仅有两个小偷,小甲和小乙,根据统计小甲偷东西的可能性是0.2,小乙偷东西的可能性是0.8。
如果小甲去偷,偷成功的概率是0.8, 如果小乙去偷,偷成功的概率是0.3。
如果村子丢了一件东西,小甲和小乙谁是嫌疑犯的可能性更大?
我们定义事件:H=丢东西,
A=小甲去偷东西,
B=小乙去偷东西,
因此,不是A就是B偷的:P(A) + P(B) = 1,
上面已经告知:小甲和小乙两人偷东西可能性 P(A) = 0.2, P(B) = 0.8;这个可以从当地的派出所的案底可以统计出来
上面已经告知:小甲和小乙两人得手的(成功的)可能性:P(H|A)=0.8, P(H|B)=0.3
(0)那么村子里丢东西的可能性就是 P(H) = P(A)P(H|A) + P(B)P(H|B) = 0.4
现在:
(1)知道了结果H发生了,是小甲偷的概率:
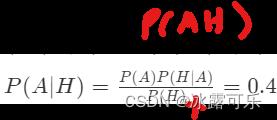
(2)知道了结果H发生了,是小乙偷的概率:

以上分析可以看出,虽然小甲得手率高,但是不经常出手偷人,小乙虽然不咋能成功,但是他是个惯犯,经常偷,所以乙偷的可能性大!
这里已然假设甲乙两人偷人的概率是独立的,他们没有关系。
朴素贝叶斯中的“朴素”怎么理解?
朴素贝叶斯中的朴素可以理解为是“简单、天真”的意思,
因为“朴素”是假设了特征之间是同等重要、相互独立、互不影响的,
但是在我们的现实社会中,属性之间并不是都是互相独立的,有些属性也会存在性,所以说朴素贝叶斯是一种很“朴素”的算法。
过于理想的算法。
什么是拉普拉斯平滑法?
拉普拉斯平滑法是朴素贝叶斯中处理零概率问题的一种修正方式。
在进行分类的时候,可能会出现某个属性在训练集中没有与某个类同时出现过的情况,
如果直接基于朴素贝叶斯分类器的表达式进行计算的话就会出现零概率现象。
为了避免其他属性所携带的信息被训练集中未出现过的属性值“抹去”,
所以才使用拉普拉斯估计器进行修正。
具体的方法是:在分子上加1,
对于先验概率,在分母上加上训练集中可能的类别数;
对于条件概率,则在分母上加上第i个属性可能的取值数
朴素贝叶斯中有没有超参数可以调?
答:没有的
朴素贝叶斯是没有超参数可以调的,所以它不需要调参,
朴素贝叶斯是根据训练集进行分类,分类出来的结果基本上就是确定了的,
拉普拉斯估计器不是朴素贝叶斯中的参数,不能通过拉普拉斯估计器来对朴素贝叶斯调参。
你知道朴素贝叶斯有哪些应用吗?
朴素贝叶斯的应用最广的应该就是在文档分类、
垃圾文本过滤(如垃圾邮件、垃圾信息等)、
情感分析(微博、论坛上的积极、消极等情绪判别)这些方面,
除此之外还有
多分类实时预测、
推荐系统(贝叶斯与协同过滤组合使用)、
拼写矫正(当你输入一个错误单词时,可以通过文档库中出现的概率对你的输入进行矫正)等。
朴素贝叶斯对异常值敏不敏感?
答:不仅不敏感,还不能去除异常值
朴素贝叶斯对异常值不敏感。
所以在进行数据处理时,我们可以不去除异常值,
因为保留异常值可以保持朴素贝叶斯算法的整体精度,
而去除异常值则可能在进行预测的过程中由于失去部分异常值导致模型的泛化能力下降。
频率学派与贝叶斯学派的差别
哲学思想完全不一样,
思考:人,生而性本善?还是性本恶,有本质的不同!!!
(1)频率学派 - Frequentist - Maximum Likelihood Estimation (MLE,最大似然估计)——人生而善,只需要找到善念。
(2)贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP,最大后验估计)——人生而为恶,后天需要教育,交换,调整改善。
频率学派和贝叶斯学派对世界的认知有本质不同:
频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范围;
而贝叶斯学派认为世界是不确定的,人们对世界先有一个预判,而后通过观测数据对这个预判做调整,我们的目标是要找到最优的描述这个世界的概率分布。
概率与期望的公式
概率:A发生的频率/天下所有事情的总数

期望:

这个x_k表示某个事件k的取值,如1,2,3,4…;
p_k 表示取值k发生的概率
按照上面的公式加和,就得到我们的期望E(x)了。
先验概率与后验概率
用“瓜熟蒂落”这个因果例子,从概率(probability)的角度说一下,
(1)先验概率:就是常识、经验所透露出的“因”的概率,即瓜熟的概率。
说白了,先验概率,就是直接告诉你这个瓜它熟了的概率。
(2)**后验概率:**就是在知道“果”之后,去推测“因”的概率,也就是说,如果已经知道瓜蒂脱落,那么瓜熟的概率是挺大的。
说白了,你已经知道瓜蒂脱掉了,那必然瓜熟了的概率很大,这是后来才知道的。
后验和先验的关系可以通过贝叶斯公式来求。
也就是:P(瓜熟 | 已知蒂落)= P(瓜熟)×P(蒂落 | 瓜熟)/ P(蒂落)

好吧
总之记住贝叶斯概率公式:
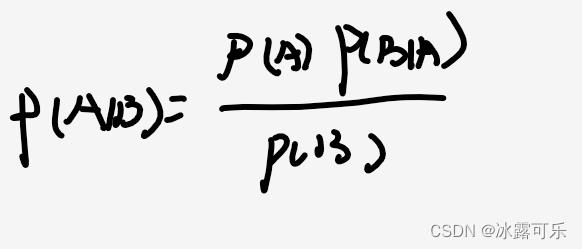
总结
提示:重要经验:
1)大厂笔试选择题经常考贝叶斯公式和朴素贝叶斯
2)没事尝尝回顾一下这些八股文
以上是关于机器学习面试题——朴素贝叶斯的主要内容,如果未能解决你的问题,请参考以下文章