分类：朴素贝叶斯算法

Posted 2021-04-25 Python大数据与人工智能

击上方

“蓝色字”

可关注我们！

今日分享：朴素贝叶斯算法

一：相关概述

朴素贝叶斯分类算法多用于文本分类（比如垃圾邮件的分类），从其名字即可知道，它是基于概率论（贝叶斯公式）的一种算法，因此如果想深入了解其原理，必须对相关的概率论知识有所了解

概率：一件事情发生的可能性

联合概率：包含多个条件，且所有条件同时成立的概率，记作：P(A,B)

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率，记作：P(A|B)；特性：P(A1,A2|B) = P(A1|B)P(A2|B)；注意：此条件概率的成立，是由于A1,A2相互独立的结果

二：贝叶斯公式

其中 W 为给定文档的特征值(频数统计,预测文档提供)，C 为文档类别

公式可以理解为：

P(C│F1,F2,…)=(P(F1,F2,…│C)P(C)) / (P(F1,F2,…))

其中C可以是不同类别

公式分为三个部分：

    1、P(C)：每个文档类别的概率(某文档类别词数／总文档词数)

    2、P(F1│C)：给定类别下特征（被预测文档中出现的词）的概率

            计算方法：P(F1│C)=Ni/N  （训练文档中去计算）

            Ni为该F1词在C类别所有文档中出现的次数

            N为所属类别C下的文档所有词出现的次数和

    3、P(F1,F2,…)     预测文档中每个词的概率（需要注意的是，在实际运算过程中，对不同的词进行计算时，该分母部分往往直接省略舍去，因为这部分的值始终是同一个值，不会因为预测词的变化而变化）

    

举个栗子

有221篇训练文档，两大类别：科技类和娱乐类，分别对这221篇文档中出现的商城、影院、支付宝、云计算这四个词进行词频统计，得到具体信息如下：

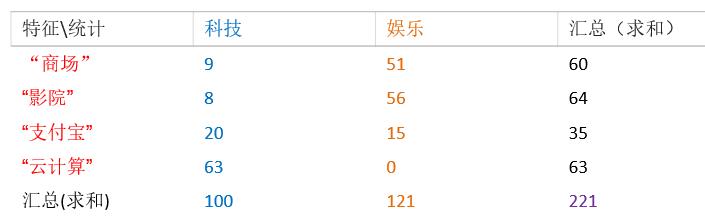
现给出一篇预测文档，其中出现了影院，支付宝，云计算这三个关键词，计算该文档属于科技、娱乐的类别概率？

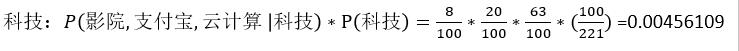
（科技）

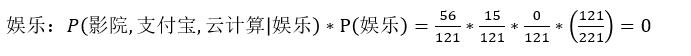
（娱乐）

问题来了，从上面的例子中我们得到娱乐概率为0，这是不合理的，如果词频列表里有很多特征词出现次数都为0，很可能计算结果都为零

解决方法：拉普拉斯平滑系数

 P(F1│C)=(Ni+α)/(N+αm)       

    

α为指定的系数一般为1，m为训练文档中统计出的特征词个数，还拿上面的例子来说， 则 m = 4，即（商场、影院、支付宝、云计算这四个特征词），所以上上述的计算公式变换为以下（当α=1时，相当于分子加1，分母加4），结果就不在计算了哈，然后去概率最大的即可作为其类别：

三：朴素贝叶斯API介绍

#sklearn朴素贝叶斯实现API
sklearn.naive_bayes.MultinomialNB

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
#朴素贝叶斯分类

alpha：拉普拉斯平滑系数

四：朴素贝叶斯优缺点

优点：在数据较少的情况下仍然有效，可以处理多类别问题。

缺点：对于输入数据的准备方式较为敏感（需要将数据处理成词向量，并且如果将输入数据中的停顿词、高频词去除掉性能会有提升，但也带来了算法的复杂性）

适用数据类型：标称型数据。（因为需要计算每个取值的条件概率，虽然也可以将连续值转化为区间，但划分区间又增加了复杂性。标称型数据：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)；数值型数据：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)）

---

---

或在后台回复：加群