译文：朴素贝叶斯算法简介（Python和R中的代码）

Posted 2021-04-25 PPV课数据科学社区

 朴素贝叶斯是一种用于分类问题的机器学习算法。它是基于贝叶斯概率定理的。主要用于涉及高维训练数据集的文本分类。几个相关的例子有：垃圾邮件过滤、情感分析和新闻文章分类。

 

它不仅因其简单而著称，而且因其有效性而闻名。它能快速构建模型和使用朴素贝叶斯算法进行预测。朴素贝叶斯是用于解决文本分类问题的第一个算法。因此，应该把这个算法学透彻。

朴素贝叶斯算法是一种用于分类问题的简单机器学习算法。那么什么是分类问题？分类问题是监督学习问题的示例。它有助于从一组类别中识别新观察的类别（子群体）。该类别是基于包含其类别成员已经已知的观察（或实例）的数据的训练集合来确定的。

分类问题是监督学习问题的示例。它有助于从一组类别中识别新观察的类别（子群体）。该类别是基于包含其类别成员已经已知的观察（或实例）的数据的训练集合来确定的。

通过这篇文章，我们将了解基础知识，数学，Python和R实现，朴素贝叶斯算法的应用和变化。与此同时，我们还将看到算法的一些优点和缺点。

 

目录

1.朴素贝叶斯的基础

2.朴素贝叶斯的数学知识

3.朴素贝叶斯的变形

4. Python和R实现

5.朴素贝叶斯的优点和缺点

6.朴素贝叶斯的应用

什么是朴素贝叶斯算法？

朴素贝叶斯算法是学习具有属于特定组/类的某些特征的对象的概率的算法。简而言之，它是一个概率分类器。朴素贝叶斯算法这个名字是怎么得来的呢？

朴素贝叶斯算法被称为“朴素”是因为它假设某个特征的出现与其它特征的出现是独立的。

例如，如果你试图根据其颜色，形状和味道识别水果，那么橙色的、球形的和味道浓烈的水果很可能是橘子。即使这些特征依赖于彼此或取决于其他特征的存在，所有这些特性可以单独地促成该果实是橙色的可能性，这就是为什么它被称为“朴素的”。

至于“贝叶斯”部分，它指的是由统计学家、哲学家托马斯·贝叶斯他名字命名的定理——贝叶斯定理，它是朴素贝叶斯算法的基础。

朴素贝叶斯算法的数学知识

如前所述，朴素贝叶斯算法的基础是贝叶斯定理或者称为贝叶斯法则或贝叶斯定律。它为我们提供了一种计算条件概率的方法，即基于事件可用的先前的事件的概率。更正式地说，贝叶斯定理被表示为以下等式：

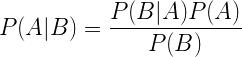
让我们首先理解式子，然后我们将看看式子的证明。上述式子的组成有：

• P(A|B)：事件A在另一个事件B已经发生的条件下的发生概率

• P(A)和P(B)：事件A发生的概率和事件B发生的概率

• P(B|A)：事件B在另一个事件A已经发生的条件下的发生概率

贝叶斯法则中的术语如下：

• A称为命题，B称为证据

• P(A)称为命题的先验概率，P(B)称为证据的先验概率

• P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率

• P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率

这就是贝叶斯定理：

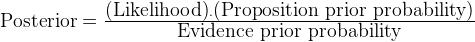
让我们举个例子来更好地理解贝叶斯定理。

假设你必须从52张卡的标准甲板上画一张卡。现在该卡是一个皇后的概率为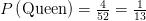。如果你给出的证据表明您已经选择该卡是一张脸卡的后验概率

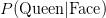可以用贝叶斯定理计算如下：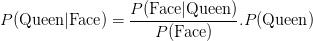

现在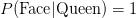，因为给出的牌是女王，这绝对是一张脸卡。我们已经计算

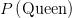。现在要计算的是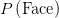，其等于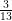，因为每一套牌都有三张脸卡。因此，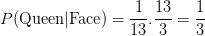

贝叶斯定理的推导

对于事件A和事件B的联合概率分布，其中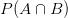为条件概率，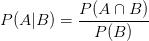

类似地，

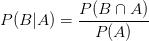
因此，

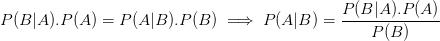
朴素贝叶斯算法的贝叶斯定理

在机器学习的分类问题，有多种特征和类，比如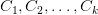。朴素贝叶斯算法的主要目的是计算具有特征向量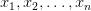且属于特定类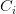的事件的条件概率。

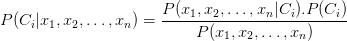
，其中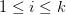现在，上面公式右边的分数的分子

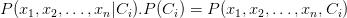
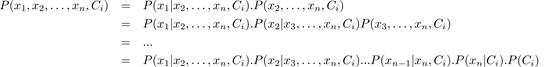
条件概率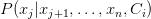

变成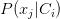。因为假设每个特征之间都是独立的。

从以上的计算和独立性假设，贝叶斯定理归纳为以下简单的表达式：

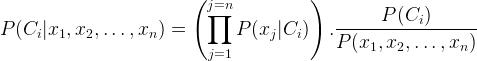，其中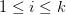   对所有的类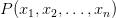，不变，我们可以简单地说，

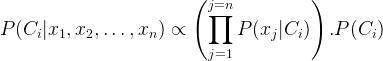，其中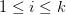

朴素贝叶斯算法如何工作？

到目前为止，我们已经了解了朴素贝叶斯算法是什么，贝叶斯定理与它有什么关联，以及该算法的贝叶斯定理的表达式是什么。让我们以一个简单的例子来理解算法的功能。假设，我们有1200个水果的训练数据集。数据集中的特征是这些：是果实是否是黄色的，果实长不长，果实甜不甜。有三个不同的类：芒果，香蕉和其他。

第1步：反对不同类别的所有功能创建一个频率表。

名称	黄色	甜	长	总计
芒果	350	450	0	650
香蕉	400	300	350	400
其他	50	100	50	150
总计	800	850	400	1200

从上表可以得出什么结论？

·        在1200个水果中，650个是芒果，400个是香蕉，150个是其他。

·        总共650个芒果中的350个是黄色的，其余的不是，等等。

·        总共1200个水果，800个水果是黄色的，850个是甜的，400个是长的。

现在，你得到一个黄色，甜的，长的水果，你必须检查它属于的类。

第2步：绘制的可能性表对类的功能。

名称	黄色	甜	长	总计
芒果	350/800 = P（芒果|黄色）	450/850	0/400	650/1200 = P（Mango）
香蕉	400/800	300/850	350/400	400/1200
其他	50/800	100/850	50/400	150/1200
总计	800 = P（黄色）	850	400	1200

第3步：计算所有类，即条件概率，在我们的例子如下：

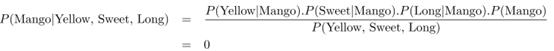
第4步：计算

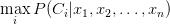
。在我们的例子中，香蕉类的概率最大，因此通过朴素贝叶斯算法，我们得到长的、甜的和黄的水果是一个香蕉。

简而言之，我们说一个新元素将属于将具有上述条件概率最大的类。

朴素贝叶斯算法的变形

根据朴素贝叶斯算法的分布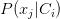，它有多种变形。三个常用的变形是

1.     高斯分布：高斯朴素贝叶斯算法假设特征的分布服从高斯分布或正态分布，也就是：

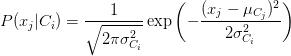
了解更多。

2.     多项式：多项式朴素贝叶斯算法适用于多元数据集。阅读更多。

3.     伯努利分布：当数据集中的要素是二值变量时，使用伯努利算法。多用于垃圾邮件过滤和成人内容检测技术。有关详细信息，请点击。

用Python和R实现朴素贝叶斯算法

让我们看看我们如何使用R和Python中的朴素贝叶斯算法构建基本模型。

R代码

要开始训练R中的朴素贝叶斯分类器，我们需要加载e1071包。

 

1	library(e1071)

R中用于实现朴素贝叶斯的预定义函数称为  naiveBayes （）。一些参数：

1	naiveBayes(formula,data,laplace=0,subset,na.action=na.pass)

·        formula：原始的式子

·        data：包含数字或因子变量的数据集

·        laplace：提供了一个平滑效果

·        subset：用于在Boolean filter上数据的选择子集

·        na.action：当数据集中有缺失值时的处理

让我们以iris数据集为例。

 

1 2 3 4 5 6 7 8

>library(e1071) >data(iris) >nB_model<-naiveBayes(iris[,1:4],iris[,5]) >table(predict(nB_model,iris[,-5]),iris[,5])#returns the confusion matrix                 setosa  versicolor virginica   setosa          50          0          0   versicolor      0          47         3   virginica        0          3        47

Python代码

我们将使用Python的scikit-learn库实现朴素贝叶斯算法。

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

>>>fromsklearn.naive_bayes importGaussianNB >>>fromsklearn.naive_bayes importMultinomialNB >>>fromsklearn importdatasets >>>fromsklearn.metrics importconfusion_matrix   >>>iris=datasets.load_iris()   >>>gnb=GaussianNB() >>>mnb=MultinomialNB()   >>>y_pred_gnb=gnb.fit(iris.data,iris.target).predict(iris.data) >>>cnf_matrix_gnb=confusion_matrix(iris.target,y_pred_gnb)   >>>print(cnf_matrix_gnb) [[50  0  0] [047  3] [0  347]]   >>>y_pred_mnb=mnb.fit(iris.data,iris.target).predict(iris.data) >>>cnf_matrix_mnb=confusion_matrix(iris.target,y_pred_mnb)   >>>print(cnf_matrix_mnb) [[50  0  0] [046  4] [0  347]]

朴素贝叶斯算法的优缺点

每件事情都有两面性。朴素贝叶斯算法也是如此。它也有优点和缺点，它们如下：

 

优点

 

• 这是一个相对容易构建和理解的算法。

• 使用该算法比许多其他分类算法能更快地预测类。

• 它使用小数据集也可以容易地训练数据。

 

缺点

 

• 如果给定没有出现过的类和特征，则该类别的条件概率估计将出现为0.该问题被称为“零条件概率问题”。这是一个问题，因为它会擦除其他概率中的所有信息。有几个样本校正技术可以解决这个问题，如“拉普拉斯校正”。

• 另一个缺点是它的特征之间独立的假设非常强。 在现实生活中几乎不可能找到这样的数据集。

应用

朴素贝叶斯算法用于多个现实生活场景，例如

1.     文本分类：它是用来作为文本分类的概率学习方法。当涉及文本文档的分类时，朴素贝叶斯分类器是已知的最成功的算法之一。如：文本文档是否属于一个或多个类别（类）。

2.     垃圾邮件过滤：这是文本分类的一个例子。这已成为区分垃圾邮件和合法电子邮件的流行机制。很多现代电子邮件服务都用贝叶斯实现垃圾邮件过滤。
许多服务器端电子邮件过滤器，例如DSPAM，SpamBayes，SpamAssassin，Bogofilter和ASSP，都使用这种技术。

3.     情感分析：它们可以用来分析微博及其评论的语气，判断是负面的，正面的还是中立。

4.     推荐系统：朴素贝叶斯算法与协同过滤相结合用来构建混合推荐系统，这有助于预测用户是否愿意提供资源。

结论

本文用一些易于理解的例子和一些专业术语来对朴素贝叶斯分类算法做一个简单的介绍。

尽管有较复杂的数学内容，朴素贝叶斯算法的实现只涉及对特定的特征和类的简单计数。一旦获得这些数字，就很容易计算概率并得出结论。

希望你现在已经熟悉了这个曾经听说过的机器学习概念。

END.

PPV课翻译，转载请联系授权

欲了解更多算法请查看以下好文

★

★

★