朴素贝叶斯简介

Posted 2021-04-25 易智能EasyAI

本文为那些想知道更多关于机器学习最简单和概率方法的人，朴素贝叶斯。

朴素贝叶斯是在监督机器学习的基础上，根据先验知识和独立假设，对数据集进行分类和预测。

朴素贝叶斯算法：

是对未知数据集进行决策的分类算法。它基于贝叶斯定理，该定理基于其先验知识描述事件的概率。

它被广泛用于在谷歌搜索，电子邮件排序，语言检测等各种应用中使用的文本分类。下图显示了NB如何实现预测。

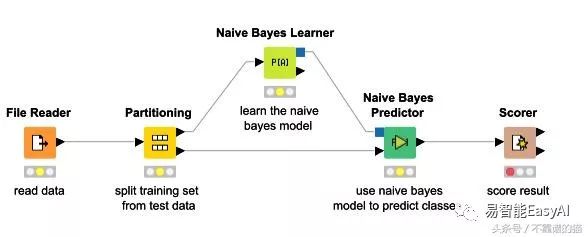
它用于检查数据集的先验概率，并提供新的概率。

对于所有数据集，先验概率总是被划分为50％-50％，并且算法的工作是基于当前存在的对象来确定它属于哪个类别标签。

例如：体重和身高是决定玩家是相扑选手还是篮球选手的参数。最初，它分为平均分配的两部分。

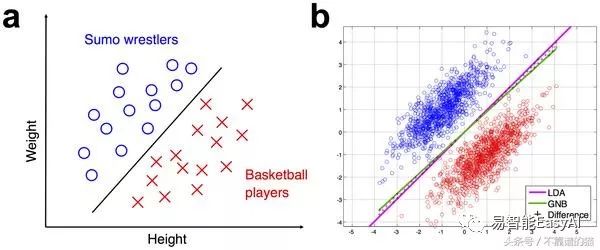
预测NB的公式：

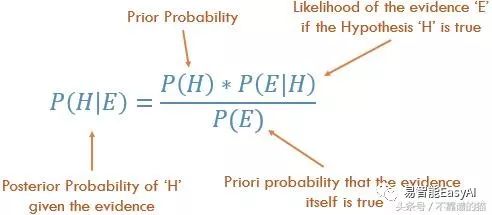
• P(H|E)是给定预测因子(E，attributes)的类(H, target)的后验概率。

• P(H)是先验概率。

• P(E|H)是预测给定类概率的可能性。

• P(E)是预测因子的先验概率。

如何使用朴素贝叶斯算法?

用例:在天气条件下和相应的目标变量“Play”(暗示Playing的可能性)。现在，我们需要根据天气情况对球员是否上场进行分类。让我们按照下面的步骤来执行它。

步骤1:首先我们找到表示下面图表中yes或no概率的表格

步骤2:查找每个类的后验概率。

问题：找出球员是否在Rainy状态下进行比赛的可能性？

P(Yes|Rainy) = P(Rainy|Yes) * P(Yes) / P(Rainy)

P(Rainy|Yes) = 2/9 = 0.222

P(Yes) = 9/14 = 0.64

P(Rainy) = 5/14 = 0.36

现在，P（Yes | Rainy）= 0.222 * 0.64 / 0.36 = 0.39这是较低的概率，这意味着比赛的机会很低。

使用朴素贝叶斯算法的场景:

• 如果你有一个中等或大型的训练数据集。

• 如果实例有多个属性。

• 给定分类参数，描述实例的属性应该是有条件独立的。

• 当内存和CPU资源有限时。

• 它的计算量更小。

朴素贝叶斯算法的利与弊?

优点:

• 容易实现

• 减少模型的复杂性

• 更少的CPU计算。

• 当数据集很小的时候表现良好。

缺点:

• 非常强烈的假设，由于这些结果是不好的，它被称为naively。

• 数据稀缺

• 现实生活中的问题，如无变量依赖。

• 当数据过大时表现不佳，假设所有特性都是独立的。