图论动态规划算法——Floyd最短路径
Posted 远洋号
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论动态规划算法——Floyd最短路径相关的知识,希望对你有一定的参考价值。
前言
推出一个新系列,《看图轻松理解数据结构和算法》,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握。本系列包括各种堆、各种队列、各种列表、各种树、各种图、各种排序等等几十篇的样子。
Floyd算法
Floyd是一种经典的多源最短路径算法,它通过动态规划的思想来寻找给定加权图中的多源点之间的最短路径,算法时间复杂度是O(n3)。之所以叫Floyd是因为该算法发明人之一是Robert Floyd,他是1978年图灵奖获得者,同时也是斯坦福大学计算机科学系教授。
核心思想
对于n个点的加权图,从加权图的权值矩阵开始,递归地更新n次最终求得每两点之间的最短路径矩阵。即加权图的邻接矩阵为$D=(d_{ij})_{n imes n}$,按一定公式对该矩阵进行递归更新,初始时矩阵为D(0),第一次,根据公式用D(0)构建出矩阵D(1);第二次,根据公式用D(1)构建出矩阵D(2);以此类推,根据公式用D(n-1)构造出矩阵D(n),D(n)即为图的距离矩阵,i行j列表示顶点i到顶点j的最短距离。
动态规划
如何理解这种动态规划算法呢?可以理解为逐一选择中转点,然后针对该中转点,所有以此为中转点的其它点都要根据规定进行更新,这个规定就是原来两点之间的距离如果通过该中转点变小了则更新距离矩阵。比如选择“1”作为中转点,原来“02”之间的距离为5,通过中转点1后(即路径变为“012”)距离为4,变小了,那么就更新距离矩阵对应的元素,由5更新为4。当图中所有顶点都被作为中转点处理以后,那么得到的最后距离矩阵就是多源最短距离矩阵了。
设$c(i,j,k)$为i到j的中间节点编号不超过k的最短距离,当k=0时,$c(i,j,0)=d_{ij}$,对于n个顶点的图,我们要求的i到j的最短距离即是$c(i,j,n-1)$。
现在我们建立$c(i,j,k)$和$c(i,j,k-1)$之间的递归关系,对于任意k,$c(i,j,k)=min(c(i,j,k-1),c(i,k,k-1)+c(k,j,k-1))$,于是可以根据该递归关系得到最终的最短路径,即中间节点编号不超过n-1的最短距离。
算法过程
从任意一条单边路径开始,所有两点之间的距离是边的权重,如果两点之间没有边相连,则权重为无穷大。即用数组
$D=(d_{ij})_{n imes n}$来记录i,j之间的最短距离,初始时,若i=j则dis[i][j]=0。若i、j两点之间相连则dis[i][j]的值为该边的权值。若i、j两点没有相连则dis[i][j]的值为无穷。对于每一对顶点u和v,看看是否存在一个顶点w使得从u到w再到v比已知的路径更短,如果存在则更新。即对所有的k值(1<k<n),计算(d[i][k]+d[k][j])的值,若其小于d[i][j],则d[i][j]=d[i][k]+d[k][j],否则d[i][j]的值不变。
神奇的五行代码
Floyd算法核心就是下列五行代码,可以体会一下,三个for循环嵌套,最外层的k即是循环取不同中转点时的情况,分别让图中每个顶点作为中转点去更新距离,完成所有循环后就是最终的最短距离矩阵。
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(d[i][k]+d[k][j]<d[i][j])
d[i][j]=d[i][k]+d[k][j];
优缺点
优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。对于稠密图效果最佳,边权可正可负。
缺点:时间复杂度比较高,不适合计算大量数据。
执行过程
对于一个拥有7个顶点的无向加权图,分别用0-6来表示图的每个顶点,每条边上的数字为对应的权重。
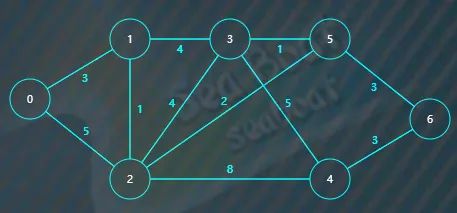
首先根据每条边的权重来初始化距离矩阵,这是一个[7x7]的矩阵,行列分别对应两个顶点,比如第0行第1列表示顶点0到顶点1,对应的值为3,即权值为3。以此类推,其它元素分别代表对应边的权重。
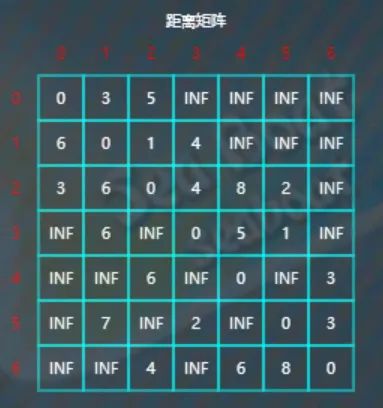
当以顶点0为中转点时
逐一查找看是否有以0为中转点使得距离更短,实际上并不用比较所有矩阵的元素,只需比较满足if (i != j && j != k && i != k)条件的元素,即都为0的对角线和中转点对应的行列不用比较,因为对角线上的元素表示顶点自己到自己的距离,所以无需比较,而中转点对应的行列表示顶点到中转点的距离,也无需比较。
比较d[1][2]与d[1][0]+d[0][2],因为1<3+5,所以不更新d[1][2]。
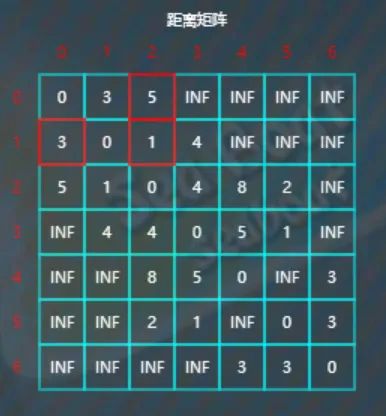
往下,比较d[1][3]与d[1][0]+d[0][3],因为4<3+INF,所以不更新d[1][3]。
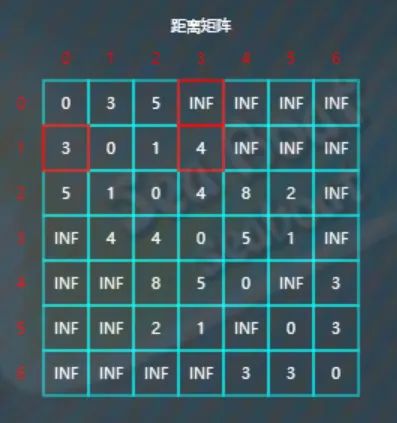
往下,比较d[1][4]与d[1][0]+d[0][4],因为INF<3+INF,所以不更新d[1][4]。接着往下d[1][5]、d[1][6]两个元素情况类似。
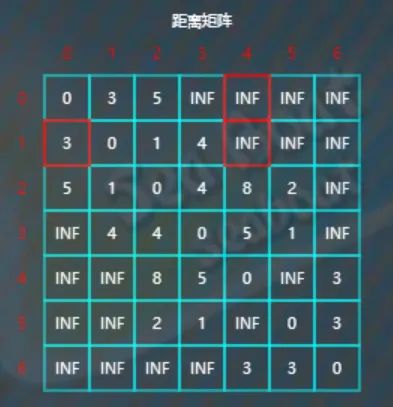
比较d[2][1]与d[2][0]+d[0][1],因为1<3+5,所以不更新d[2][1]。
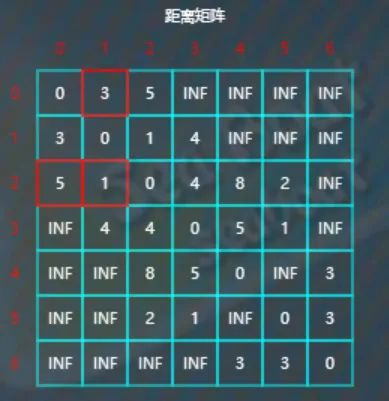
往下,比较d[2][3]与d[2][0]+d[0][3],因为4<5+INF,所以不更新d[2][3]。
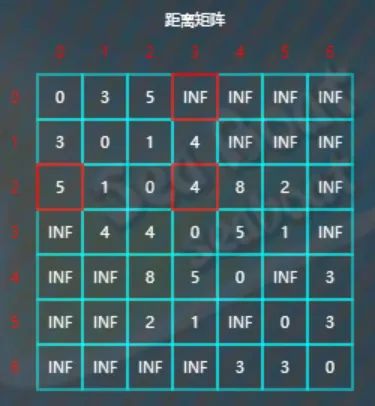
往下,比较d[2][4]与d[2][0]+d[0][4],因为8<5+INF,所以不更新d[2][4]。
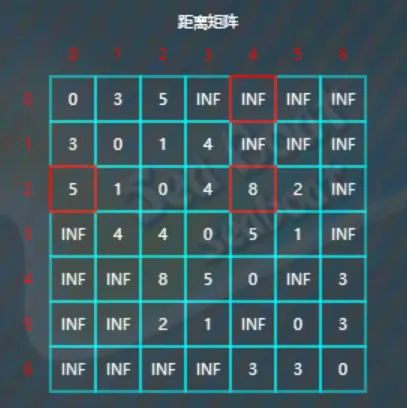
往下,比较d[2][5]与d[2][0]+d[0][5],因为2<5+INF,所以不更新d[2][5]。
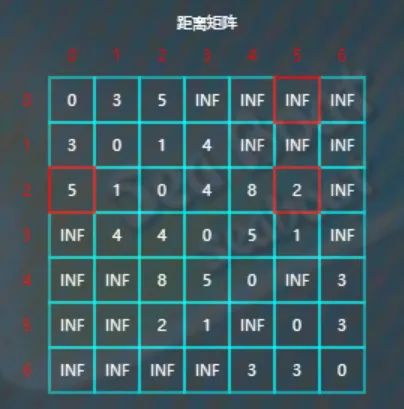
往下,比较d[2][6]与d[2][0]+d[0][6],因为INF<5+INF,所以不更新d[2][6]。
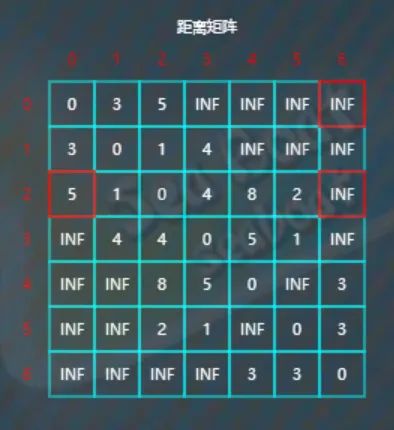
比较d[3][1]与d[3][0]+d[0][1],因为4<INF+3,所以不更新d[3][1]。
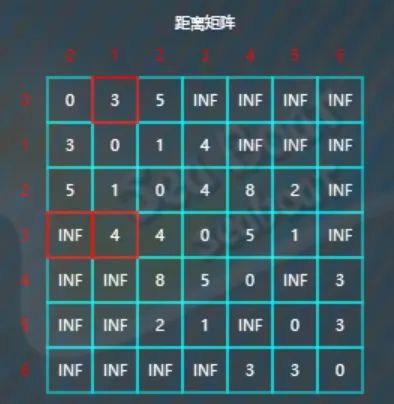
类似地,剩下的元素全部都不更新,最后比较完d[6][5]与d[6][0]+d[0][5]后即完成了以0作为中转点的全部比较工作。
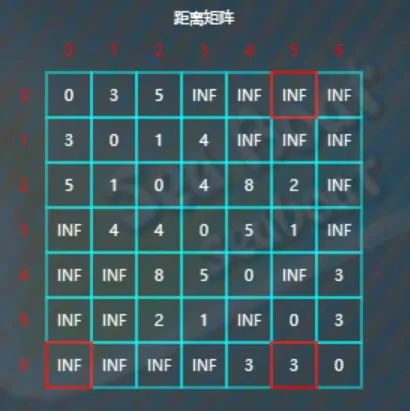
当以顶点1为中转点时
逐一查找看是否有以1为中转点使得距离更短,比较d[0][2]与d[0][1]+d[1][2],
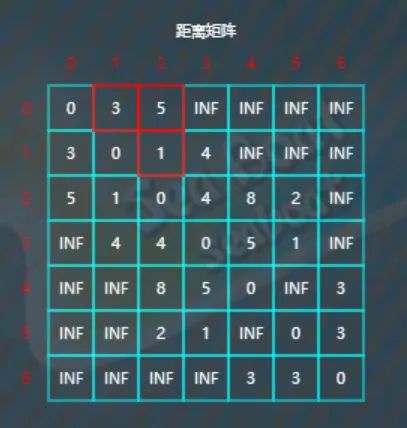
因为5>3+1,所以将d[0][2]的值更新为4。
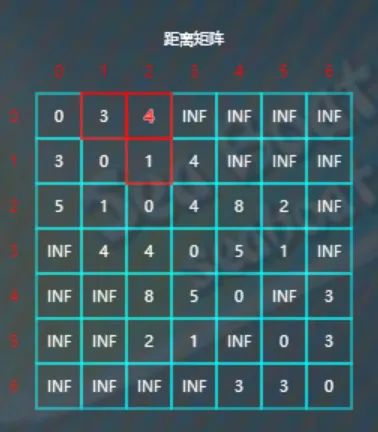
比较d[0][3]与d[0][1]+d[1][3],
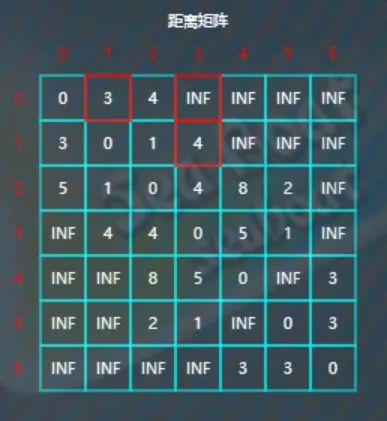
因为INF>3+4,所以将d[0][3]的值更新为7。
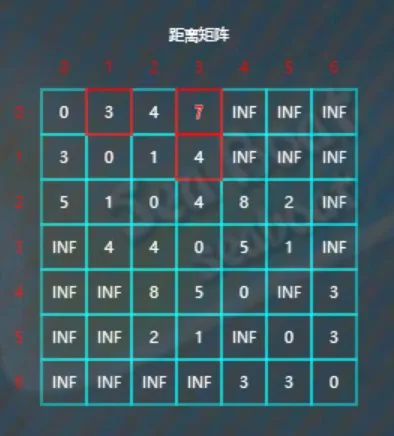
第0行接着的三个元素都不更新,到第2行后,比较d[2][0]与d[2][1]+d[1][0],
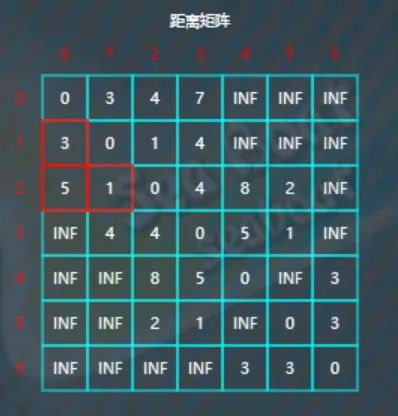
因为5>1+3,所以将d[2][0]的值更新为4。第二行剩余的元素都无需更新。
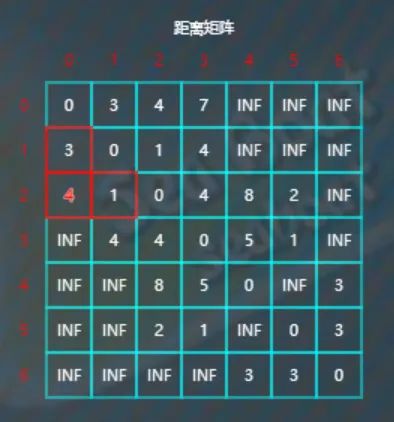
开始第3行,比较d[3][0]与d[3][1]+d[1][0],
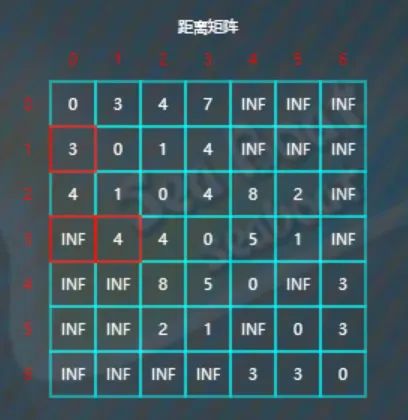
因为INF>4+3,所以将d[3][0]的值更新为7。
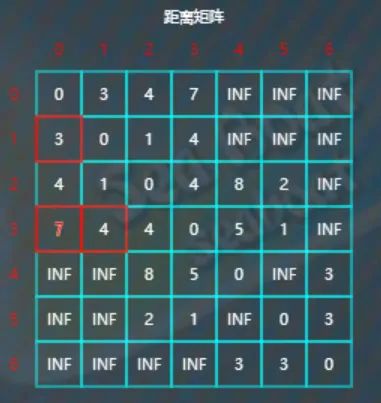
接着以顶点1作为中转点时剩余的全部元素都无需更新。
当以顶点2为中转点时
逐一查找看是否有以2为中转点使得距离更短,比较d[0][1]与d[0][2]+d[2][1],因为3<4+1,所以d[0][1]不更新。
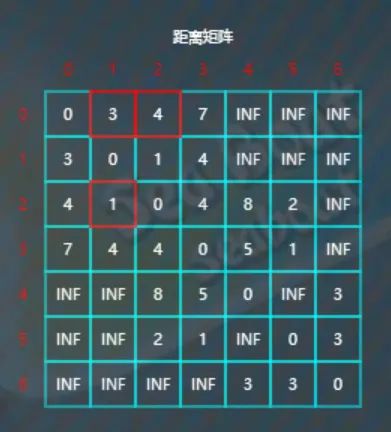
比较d[0][3]与d[0][2]+d[2][3],因为7<4+4,所以d[0][3]不更新。
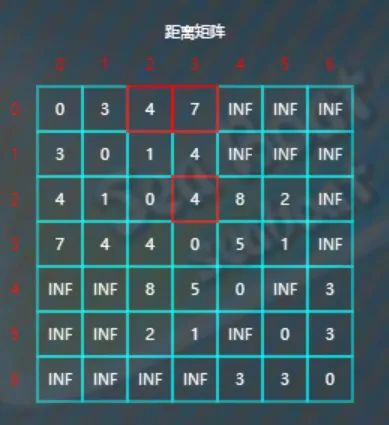
比较d[0][4]与d[0][2]+d[2][4],
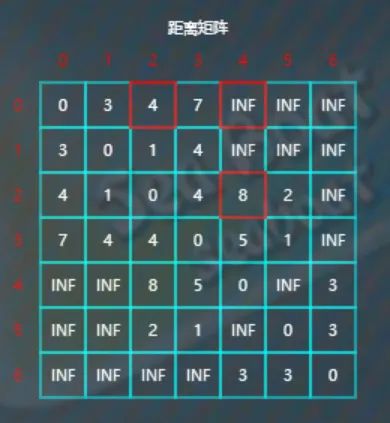
因为INF>4+8,所以将d[0][4]的值更新为12。
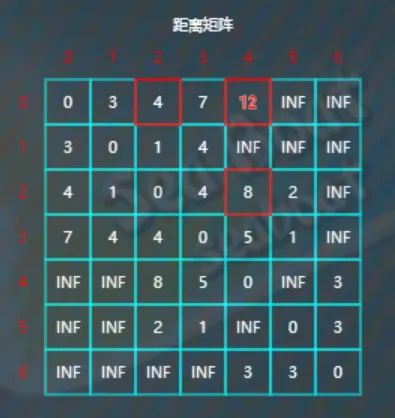
类似地,对以顶点2作为中转点的全部剩余元素进行比较更新。
当以顶点3为中转点时
逐一查找看是否有以3为中转点使得距离更短,比较d[0][1]与d[0][3]+d[3][1],因为3<7+4,所以d[0][1]不更新。
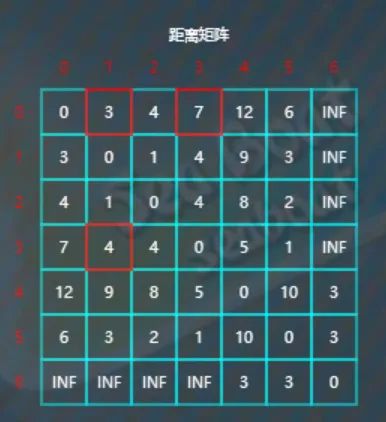
比较d[0][2]与d[0][3]+d[3][2],因为4<7+4,所以d[0][2]不更新。
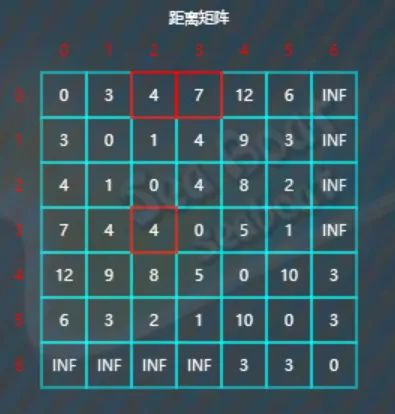
类似地,对以顶点3作为中转点的全部剩余元素进行比较更新。
当以顶点4为中转点时
逐一查找看是否有以4为中转点使得距离更短,比较d[0][1]与d[0][4]+d[4][1],因为3<12+9,所以d[0][1]不更新。
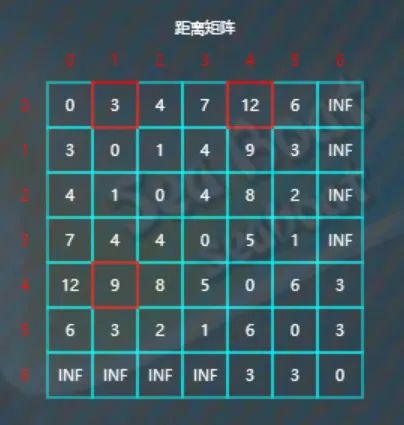
比较d[0][2]与d[0][4]+d[4][2],因为4<12+8,所以d[0][2]不更新。
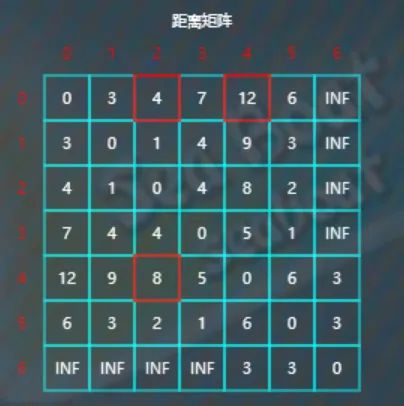
类似地,对以顶点4作为中转点的全部剩余元素进行比较更新。
当以顶点5为中转点时
逐一查找看是否有以5为中转点使得距离更短,比较d[0][1]与d[0][5]+d[5][1],因为3<6+3,所以d[0][1]不更新。
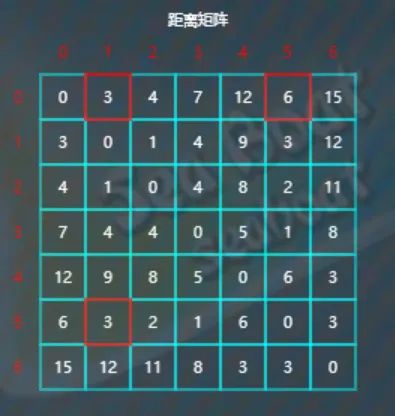
比较d[0][2]与d[0][5]+d[5][2],因为4<6+2,所以d[0][2]不更新。
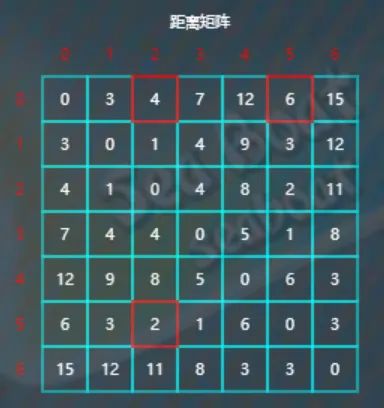
类似地,对以顶点5作为中转点的全部剩余元素进行比较更新。
当以顶点6为中转点时
逐一查找看是否有以6为中转点使得距离更短,比较d[0][1]与d[0][6]+d[6][1],因为3<9+6,所以d[0][1]不更新。
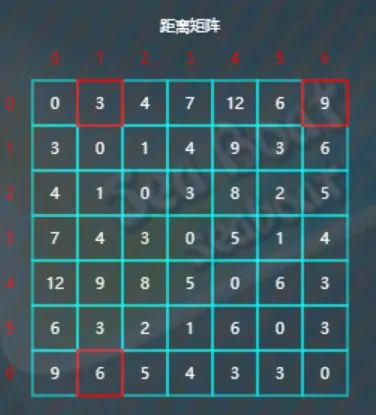
比较d[0][2]与d[0][6]+d[56][2],因为4<9+5,所以d[0][2]不更新。
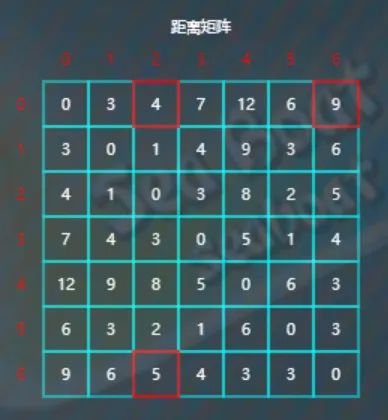
类似地,对以顶点6作为中转点的全部剩余元素进行比较更新。
最终矩阵
将所有顶点作为中转点处理后,最终得到了一个矩阵,这个矩阵就是图的每个顶点两两最短距离矩阵。比如a[0][4]=12就是顶点0到顶点4的最短距离为12。同时可以看到距离矩阵是以对角线为轴对称的。
--------------------------------------
跟我交流:
-------------推荐阅读------------
以上是关于图论动态规划算法——Floyd最短路径的主要内容,如果未能解决你的问题,请参考以下文章
a*算法求最短路径和floyd还有dijsktra算法求最短路径的区别?