经典动态规划问题 -- 青蛙上台阶与 python 的递归优化

Posted 2021-04-18 小脑斧科技博客

1. 问题

一大早，前同事在微信上给出了个题：
一只青蛙上台阶，一次只能上一个或两个台阶，如果总共有3个台阶，那么有三种上法：

1. 111 — 每次上一个台阶

2. 21 — 先上两个台阶，再上一个台阶

3. 12 — 先上一个台阶，再上两个台阶

那么对于 n 个台阶，有多少种上法呢？

2. 思路

乍一看觉得并不难，只要简单的罗列就好了，题目描述不也是这么描述的嘛？但是仔细一想，罗列的情况十分复杂。
突然想到单源最短路问题，其实这就是经典的动态规划问题 — 单源最短路问题的一个变种，我们如果把每个台阶想象成一张有向加权图的点，每个点都由他前面两个点指向他，权重分别为1和2，这就转化成了一个经典动态规划问题了 — 由点0到点n有多少种走法。

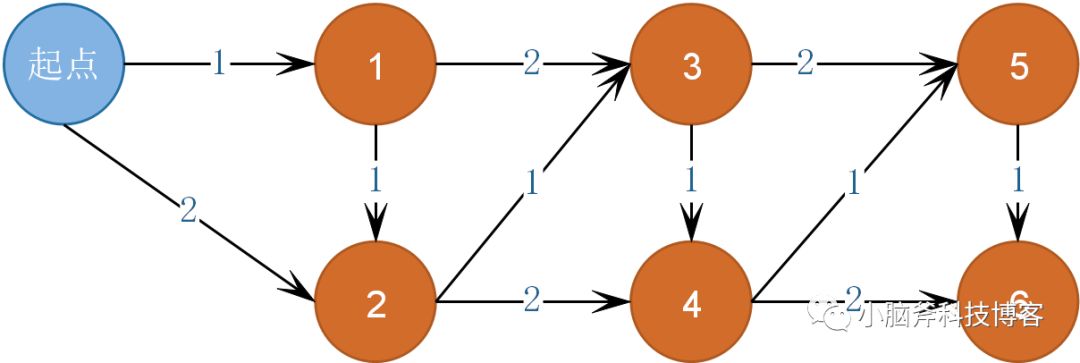
显然，f(n)＝f(n-1)＋f(n-2)，同时，f(1)＝1，f(2)＝2。
写代码就简单多了，用一个递归即可。

3. 代码实现

# -*- coding:utf-8 -*-
import time

def jumpFloor(number):
    if number == 0:
        return 0
    if number == 1:
        return 1
    if number == 2:
        return 2
    return jumpFloor(number - 1) + jumpFloor(number - 2)

if __name__ == '__main__':
    starttime = time.time()
    print(jumpFloor(40))
    print('耗时：' + str(time.time() - starttime))

执行结果：

165580141
耗时：30.301055192947388

• 什么？仅仅40个台阶，就要花30多秒来计算，再继续增加台阶数，时间将会成倍增长，这怎么受得了呢？

4. 尾递归

4.1. 讲解

上述递归过程之所以耗时，是因为每一次递归都需要在栈中开辟新的调用栈执行子方法，在栈的反复开辟、销毁过程中，不仅耗时激增，最为关键的是，反复的栈开辟让内存占用率急剧增长。
在 C 语言中，编译器有一个概念 — 尾递归，当编译器检测到一个函数调用的递归是函数的最后一行，那么编译器就覆盖当前的栈而不是在当前栈中去创建一个新的栈。
下面我们将上述代码改为尾递归的方式，基本思路是通过一个参数来保存上次执行结果，另一个参数保存累计值。

4.2. 代码

# -*- coding:utf-8 -*-
import time

def jumpFloor(number):
    if number == 0:
        return 0
    if number == 1:
        return 1
    if number == 2:
        return 2
    return solute(number, 0, 1)

def solute(number, a, b):
    if number == 0:
        return b
    return solute(number-1, b, a+b)

if __name__ == '__main__':
    starttime = time.time()
    print(jumpFloor(400))
    print('耗时：' + str(time.time() - starttime))

4.3. 运行结果

284812298108489611757988937681460995615380088782304890986477195645969271404032323901
耗时：0.0005254745483398438

我们看到，运行 400 级台阶的计算结果都只有 0.5 毫秒，优化效果相当明显。

5. 手动实现 python 的尾递归优化

上述代码如果将台阶层数增加到几千就会抛出异常：

RecursionError: maximum recursion depth exceeded in comparison

我们调试一下：

可以看到，python 解释器并不会像 C 语言编译器一样对尾递归进行优化。
上述代码之所以能够让时间复杂度、空间复杂度大幅下降，其唯一的原因是将原有的两次创建栈、压栈、销毁的一系列工作变为了一次，而问题并没有从根本上解决。
怎么才能像 C 语言一样，在每次递归调用完成后，自动清理原有的栈呢？
在捕获异常后，作为异常处理的一个环节，python 解释器会自动清理原有的栈，那么通过 python 的异常机制，我们就可以实现上述功能。

# -*- coding:utf-8 -*-
import sys
import time

def jumpFloor(number):
    if number == 0:
        return 0
    if number == 1:
        return 1
    if number == 2:
        return 2
    return solute(number, 0, 1)

class TailRecurseException(Exception):
    def __init__(self, args, kwargs):
        self.args = args
        self.kwargs = kwargs

def tail_call_optimized(g):
    def func(*args, **kwargs):
        f = sys._getframe()
        if f.f_back and f.f_back.f_back and f.f_back.f_back.f_code == f.f_code:
            raise TailRecurseException(args, kwargs)
        else:
            while 1:
                try:
                    return g(*args, **kwargs)
                except TailRecurseException as e:
                    args = e.args
                    kwargs = e.kwargs
    return func

@tail_call_optimized
def solute(number, a, b):
    if number == 0:
        return b
    return solute(number-1, b, a+b)

if __name__ == '__main__':
    starttime = time.time()
    print(jumpFloor(4000))
    print('耗时：' + str(time.time() - starttime))

5.1. 讲解

执行结果：

64574884490948173531376949015369595644413900640151342708407577598177210359034088914449477807287241743760741523783818897499227009742183152482019062763550798743704275106856470216307593623057388506776767202069670477506088895294300509291166023947866841763853953813982281703936665369922709095308006821399524780721049955829191407029943622087779296459174012610148659520381170452591141331949336080577141708645783606636081941915217355115810993973945783493983844592749672661361548061615756595818944317619922097369917676974058206341892088144549337974422952140132621568340701016273422727827762726153066303093052982051757444742428033107522419466219655780413101759505231617222578292486081002391218785189299675757766920269402348733644662725774717740924068828300186439425921761082545463164628807702653752619616157324434040342057336683279284098590801501
耗时：0.014540433883666992

我们通过装饰器的一层封装，每一次祖父调用与当前调用相同时就标志着递归的发生，因为父调用是装饰器中的调用，祖父调用与当前调用都是原代码中的函数调用，相同就说明了递归的发生。
通过抛出异常清理栈空间，同时异常类中记录了当前参数，捕获异常后继续使用当前参数调用，这就解决了栈深度不断增加的问题。

• 需要注意的是，原代码必须是尾递归的方式才可以用该装饰器优化，否则将导致后续代码无法执行，从而得到错误的结果

6. 终极优化 — 迭代

6.1. 思路

上述的所有问题其实都是递归引起的，而任何一个递归的方法都可以转换为迭代法，尤其是我们本文的这个问题：

f(n)＝f(n-1)＋f(n-2)

这不就是斐波那契数列吗？
哈哈，可是如果我们开篇就使用迭代来完成，那就无法引出这么多优化的思路了。

6.2. 代码

# -*- coding:utf-8 -*-
import time

def jumpFloor(number):
    i = 1
    j = 2
    if number == 0:
        return 0
    if number == 1:
        return i
    if number == 2:
        return j
    r = 0
    for x in range(3, number + 1):
        r = i + j
        if x % 2:
            i = r
        else:
            j = r
    return r

if __name__ == '__main__':
    starttime = time.time()
    print(jumpFloor(40))
    print('耗时：' + str(time.time() - starttime))

6.3. 执行结果

165580141
耗时：0.0

所以还是迭代的方法简单明了，同时也拥有着最高的性能，推荐大家尽量使用迭代的方法来解决问题。
虽然有些问题通过递归的方法可以更容易理解，但先写出递归的代码，再转化为迭代的方法也非常简单。

7. 微信公众号