动态规划的部分总结

Posted 2021-04-18 slow learning

最经典的动态规划问题就是Fibonacci 数列，它长这样：

1,1，2,3，5,8，13,21……，其中从第三项开始，每一项都等于前两项之和。用公式表示如下

F0=1,F1=1,Fn=Fn-1+Fn-2

一个标准的递归问题，直接用python翻译过来就是

def fib(n):
    if n==0:
        return 1
    if n==1:
        return 1
 return fib(n-1)+fib(n-2)

让我们来看看它的执行时间，分别代入参数n=10,n=20,n=30,每个跑100次，查看对应的时间

从上面的时间可以看出，当n越来越大的时候，这个函数的执行效率非常低，让我们来画个图看一下它执行比较慢的原因

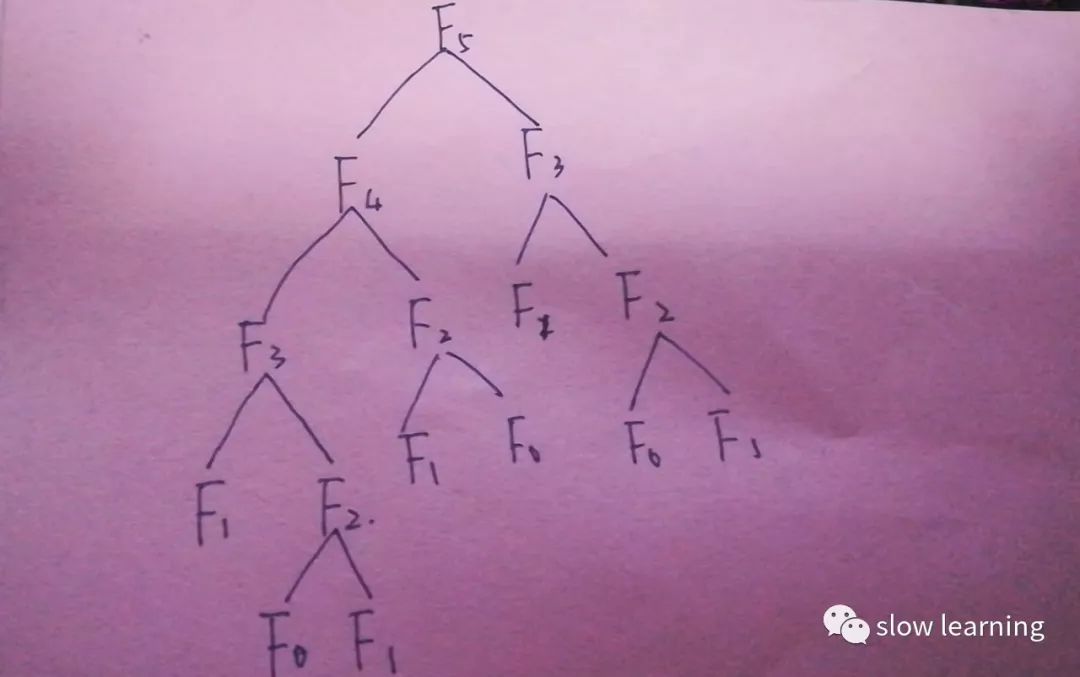
以F5为例，要计算F5,就需要把它拆分为计算F4和F3两个子问题，然后再一步步往下分拆，在上面这张图中，我们可以看到，要计算F5,其中F2被计算了3次，F3被计算了2次，这样当数值越大的时候，子问题需要被重复计算的次数增多，导致了效率变慢。

这也是动态规划的问题的标志，动态编程通过高度重叠的子问题结构帮助我们解决递归问题。

下面我们换个思路，利用缓存来存储子问题，

若缓存中包含于某个输入相对应的结果，那么从缓存中返回该值，直接翻译成python如下

def fib(n,cache=None):
    if n==0:
        return 1
    if n==1:
        return 1
    if cache is None:
        cache={}
    if n in cache:
        return cache[n]
    result=fib(n-1,cache)+fib(n-2,cache)
    cache[n]=result
    return result

查看对应的运行时间

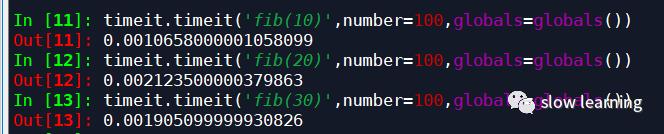
我们可以看出时间缩短了很多，空间复杂度为O(n),因为计算Fn,需要保存从F0到Fn-1的值

我们还能做的更好吗，答案是，可以

自下而上的方法

这次我们再来看一下调用树图，这次，我们每个子问题只显示一次，这意味着，如果两个不同的问题有相同的子问题，那么这个子问题将有两个指向自己的箭头

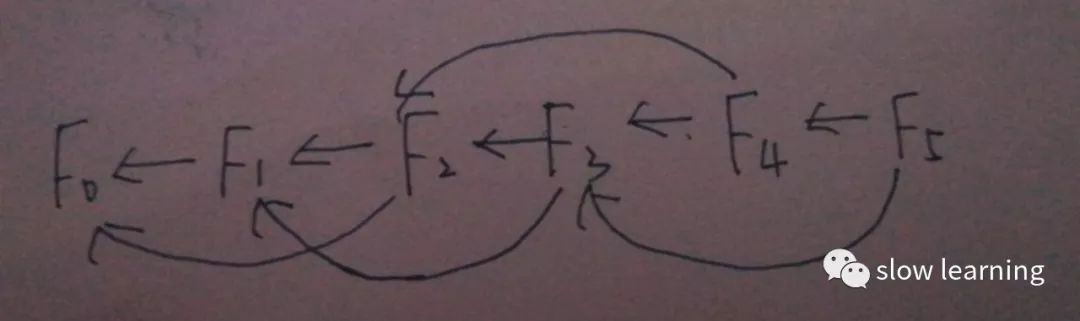
从上图中可以看出，总共有n个子问题，另外，这是一个有向无环图。这意味着以下几点：

1 每个子问题都有节点对应，并且子问题与子问题之间有边相连

2 每条边都有一个方向，表示与它相关的子问题是哪一个。

3 这个图形不是个闭环，就是没有子问题从自身开始，又结束在自己这个地方，否则的话会导致一个问题，就是我们在计算这个问题的时候，还要先计算它自身！

有向无环图具有可线性化的属性，意味着你可以按照顺序遍历节点，遵循着箭头的方向，并且这样的话，你可以仅仅保留你需要计算的问题和它对应的两个子问题的结果，翻译成python

def fib(n):
    a=1
    b=1
    for i in range(2,n+1):
        a,b=b,a+b
    return b

这里，空间复杂度变成了一个常数，这相对于之前的方法来说是一个进步。

房屋抢劫问题

现在我们已经有了一个解决子问题的框架，下面让我们将这个框架用于更复杂的问题中。假如你是一个劫匪，碰到了一排您要抢的房屋，每个房间里都有数值不等的财物，但是由于房屋的安全设计问题，若抢劫两个相邻的房间会被主人抓到，那么你最多能抢到的财物为多少？

将问题分割成一个个子问题

问题的关键是确定子问题是什么

对于房间i,你有两种选择，

一个是进去拿对应的财物，那么在这之前你能接触到的最大房间号是i-2,此时，你的财物数量会增加vi,

二，选择不进入，那么，在这之前你能接触到的最大房间号是i-1,此时，你的财物数量不会增加。

用公式表示

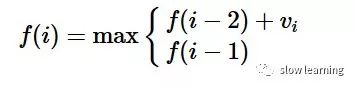
类似于Fib问题，我们也可以画出相关的有向无环图，同样的，这个问题的时间复杂度是O(n)，空间复杂度是O(1)，翻译成python如下

def house_robber(house_values):
    a=0
    b=0
    for val in house_values:
        a,b=b,max(b,a+val)
    return b

若有5间房，里面的财物数值分别为，3,10,3,1,2，那么夺取的财物数量最多为

与我们手动计算的结果相符合（备注，这里面的初始值与fib问题不同，因为，若只有一间或者两间房时，是偷不到财物的）

换零钱问题

刚才的问题都是一维问题，我们在其中迭代的都是子问题的线性序列。下一个是二维结构

这个问题的大意是若您有一定数额的纸币，需要替换对应的零钱，请问您怎么换才能使得换到的零钱的个数最少，这里面涉及到两个维度，每个零钱的对应的数值di和对应的个数c

假设有1元，5元，12元，19元四个面值的硬币，想凑成一个16元，那么有以下几种方法

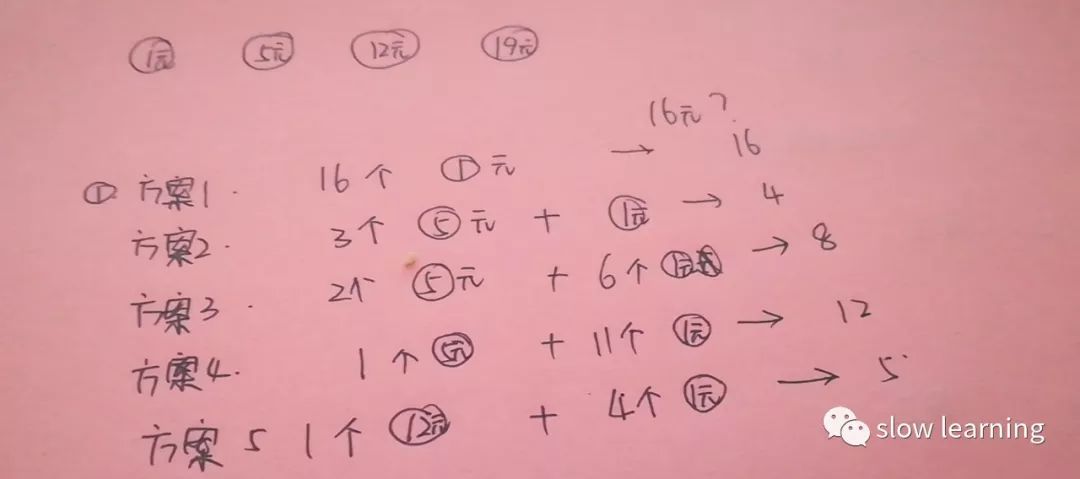
由上面可以看出，用3个5元加上一个1元所对应的硬币个数最少

将问题分拆成子问题

1 使用12元面值

从剩余的1,12,5中组合出4元

2 不适用12元面值

从剩余的1,5中组合出16元

定义递归关系

我们要定义的功能需要两个输入，允许使用的面额子集和要达到的目标值，考虑按照升序排列，那么我们可以用i表示我们只考虑d0,d1,...di面额，不考虑后面那些。定义一个函数f(i,t)其中t代表面额最大的为di的组合所需要的最小硬币数量。

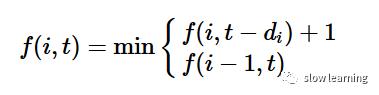
下面举个例子

在下面的示例中，存在三种面额：d2 = 3，d1 = 2和d0 = 1，以从左到右的递减值排列。最终目标值为5。但所有中间值从下到上的降序排列。因此，我们想要的答案在表格的左下方。

针对此问题的DAG有点复杂，因此我们将一次逐步构建它。首先，让我们定义图表的二维结构，并显示所需解决方案的位置。每个单元格由两个数字索引:(i,t)，其中i表示所考虑的最大面额的索引，t表示当前目标值。

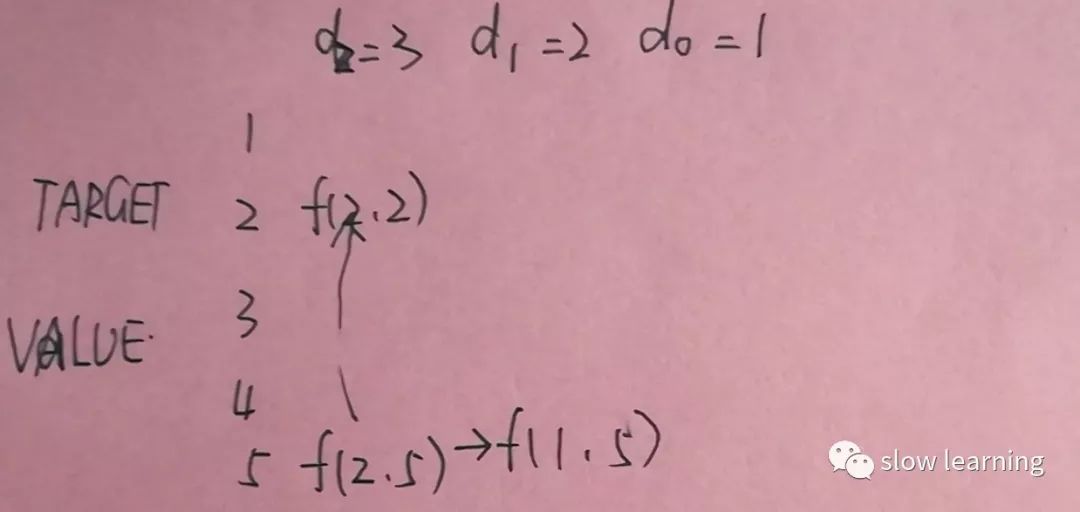
从上图可以看出，我们可以选择面值最大的硬币在同一列移动，也可以忽略最大硬币，将这列向右移动，第二步，继续刚才的操作

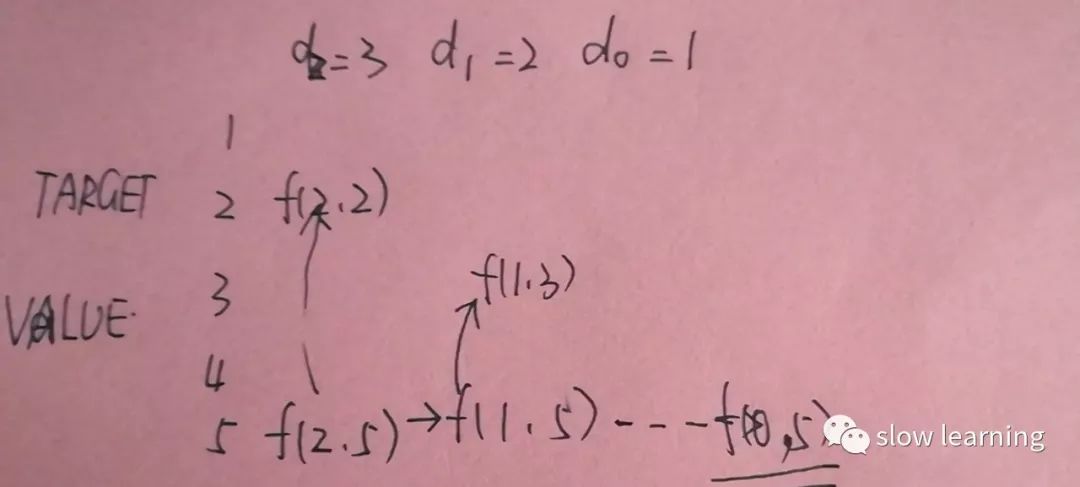
从上图中，子问题（2,5）可以用（2,2），（1,5）表示，但是子问题（2,2）中的面额3大于2,所以只能忽略最高面额d2,选择d1,而子问题（1,5）可以拆成子问题（1,3），（0,5）

当子问题到达（0,5）时，我们只能使用当前面额，因为没有其他面额比1更小，因此我们可以做的就是向上移动。依次类推，直到得出正确结果。

自下而上的计算

通过这个图，我们可以看出任何单元格仅仅取决于同一列的上方单元格和右侧列中单元格，这意味着我们可以用这种方式计算子问题

从最右边列开始，一次计算一列的值，在每一列中，从底部到顶部计算值。

计算下一列中，请保留之前计算列中的值，但是请注意，不是所有的值都是必须的，确定哪些需要，哪些不需要不是一件容易的事情。

在此，我们可以通过缓存来记录那些需要记录的值，以免重复计算。翻译成python 如下

import math
def coins(denominations,target):
    cache={}
    def subproblem(i,t):
        if (i,t) in cache:
            return cache[(i,t)]
        val=denominations[i]
        if val>t:
            choice_take=math.inf
        elif val==t:
            choice_take=1
        else:
            choice_take=1+subproblem(i,t-val)
        choice_leave=(math.inf if i==0 else subproblem(i-1,t))
        optimal=min(choice_take,choice_leave)
        cache[(i,t)]=optimal
        return optimal
    return subproblem(len(denominations)-1,target)

尽管使用缓存来减少计算数量，但是该数量仍然受图中子问题总数的限制。因为该问题的运行时间和空间复杂度为O(nc)，其中n是面额，c是目标值。

概况的说，动态编程是一种允许高度概况重叠子问题结构来解决递归问题的技术。如果要应用于此类问题，一般步骤如下：

1 确定子问题，通常每个步骤都会有一个选择，每个选择都会引入比较小的子问题的依赖、

2 写下递归关系

3确定子问题的顺序，绘制依赖图通常是有用的，通常按照顺序解决子问题来实现递归关系