动态规划（Dynamic Programming）总结

Posted 2021-11-24 敲码的钢珠

做了一部分的动态压缩的题目，来整理归纳一下。

（仅仅是以初学者的视角出发，还有很多不足和欠缺的地方，也希望各路大神指正，以后遇到新的dp类问题再来补充吧(っ °Д °;)っ）

动态规划主要应用于解决最优解的问题，这类问题往往具有局部最优子结构，一般的dp还由重复子问题，而且存在仅依赖于前一个或者前几个状态的状态迁移方程，利用分治与递归的算法思想，可以实现动态规划自底向上的实现结果的求解。

动态规划的优点：

动态规划的优点主要在于其在实现以递归为基础的算法时，避免使用函数层层递归的结构，而是跳脱出来利用数组存储和双重循环来进行记忆化递归，从而在需要的时候直接调用该结果，避免无用的重复计算，提高程序执行的效率。

经典DP例题解析与实现：

比如经典的斐波那契数列，就可以简单得通过动态规划来实现，避免了重复的递归和深度的过度挖掘。

请看代码：

/* 动态规划算法思想实现斐波那契 记忆化递归 循环展开实现 局部->整体 */
#include <iostream>

using namespace std;

const int maxn = 50 + 5;

int main() {
	int n;
	cin >> n;
	int F[maxn];
	F[1] = F[2] = 1;
	for (int i = 3; i <= n; i++) {
		F[i] = F[i - 1] + F[i - 2];
	}
	cout << F[n] << endl;
	return 0;
}

如果不用循环的动态规划，而是普通的递归，则会做很多无用功，效率大打折扣。

int fibonacci(n)
  if n==0||n==1
    return 1
  return fibonacci(n-2)+fibonacci(n-1)

在这类动态规划中，递推公式（也可以叫状态转移方程）的建立是实现dp的基础，也是关键。

比如下面这一道经典的最长公共子序列的动态规划的题目（LCS），要求俩个字符串X、Y的最长公共子序列，由题意得出如下的递推方程，那么这一道题可以轻松解决。

 自己优化完成的代码如下：

/* LCS 问题framework Dynamic Programming 循环展开&记忆化递归 分治与递归求解最优解 */
#include <iostream>
#include <string>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn = 1000 + 5;

int lcs(string x, string y) {
	int m = x.length();
	int n = y.length();
	x = ' ' + x;
	y = ' ' + y;
	int dp[maxn][maxn];
	memset(dp, 0, sizeof(dp));
	int ans = 0;
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			if (x[i] == y[j]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
			ans = max(ans, dp[i][j]);
		}
	}
	return ans;
}

int main() {
	int n;
	string x, y;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> x >> y;
		cout << lcs(x, y) << endl;
	}
	return 0;
}

类似地，这一道非常非常经典的矩阵链乘法的程设题目也同样地可以类似得解决，另外，在这里要补充一点，在解析矩阵链乘法的数学表达式的时候，可以借助stack这样一个数据结构巧妙得实现。

同样是最优解，具有局部最优子结构，分析可得：

在得出本题的递推公式的时候，对数学分析也提出了一定的要求，代码实现充分体现题意和数据内涵，精妙优化如下：

/* 矩阵链乘最优解Framework DP 循环实现&记忆化递归 分治与递归 数学分析 细节处理代码简化 */
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn = 100 + 5;

int main() {
	int n;
	cin >> n;
	int p[maxn];
	int dp[maxn][maxn];
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		cin >> p[i - 1] >> p[i];
	}
	for (int l = 2; l <= n; l++) {
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			dp[i][j] = 1 << 25;
			for (int k = i; k < j; k++) {
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j]);
			}
		}
	}
	cout << dp[1][n] << endl;
	return 0;
}

另外，所有的DP一定别忘了预处理与初始化，这很重要！o(￣┰￣*)ゞ

 以上是一般的经典DP，掌握了这样的设计或者编程技巧，我们的动态规划可以到更高一层。

高阶的状态迁移DP

硬币问题，在普通的硬币问题中，若面值类似于1、5、10、50、100等，在求所付硬币的最少枚数的时候，可以逐步减去最大面值，基于一直贪心法，但当面值随机且不定变化的时候，这种情况下的最优解就需要借助dp了，还是具有局部最优子结构的。请看状态迁移方程：

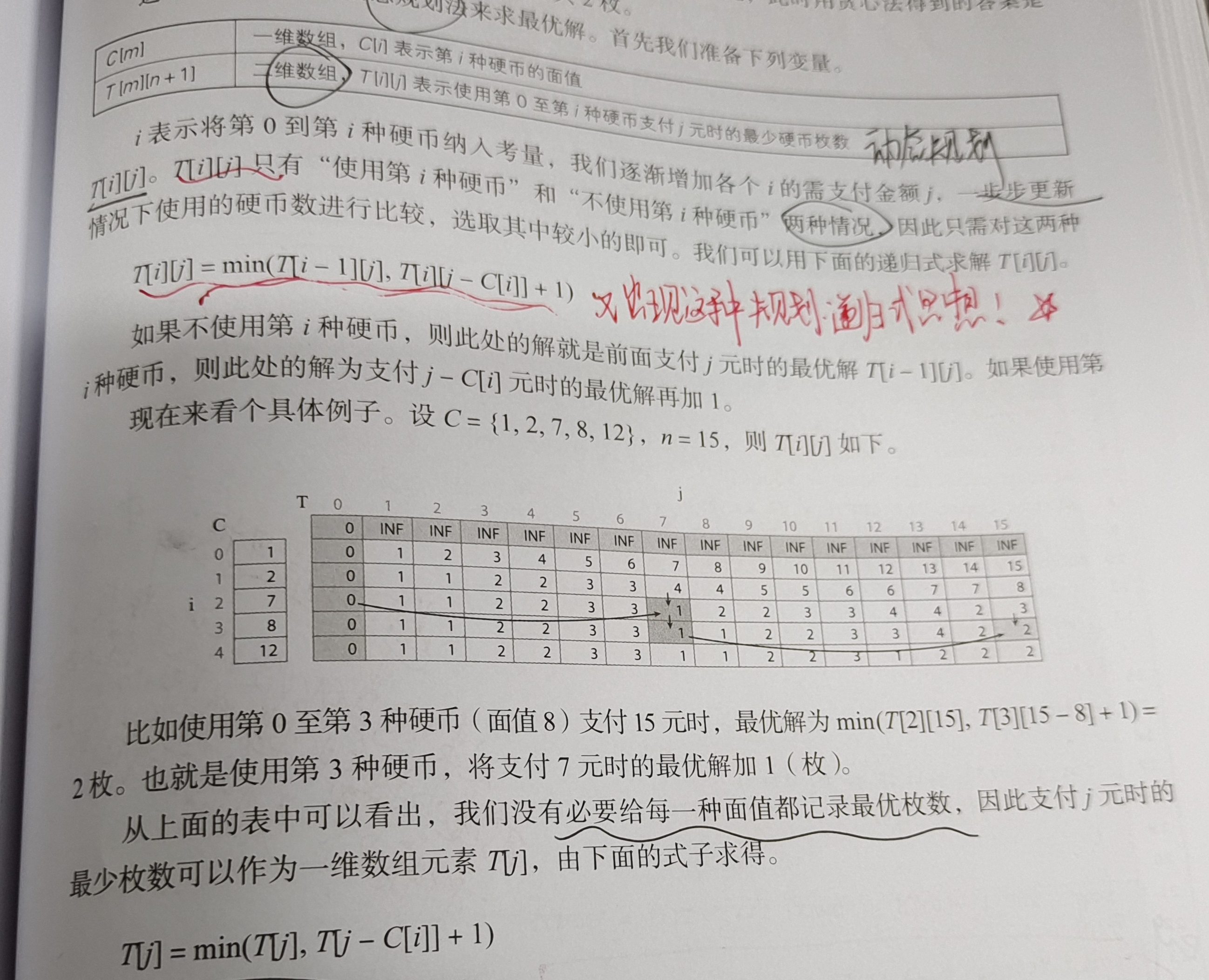
解决关键是抽象出递推模型，对于每一种状态都可以找到前一种状态来对应或者迁移。

代码如下，很精简，也很好理解，带入每一个变量和结构的被赋予的具体实际应用意义即可：

/* 硬币问题的动态规划 循环遍历下的记忆化递归 最优解 状态转移方程 编程技巧 */
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1 << 30;
const int N = 50000 + 5;
const int M = 20 + 5;

int mon[M]; 
int dp[N];

int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int c;
		cin >> c;
		mon[i] = c;
	}
	for (int i = 0; i < N; i++) {
		dp[i] = maxn;
	}
	dp[0] = 0;
	for (int i = 0; i < m; i++) {
		for (int j = 0; j + mon[i] <= n; j++) {
			dp[j + mon[i]] = min(dp[j + mon[i]], dp[j] + 1);
		}
	}
	cout << dp[n] << endl;
	return 0;
}

 再来看一道再熟悉不过的经典DP吧，0—1背包问题（应该是背包系列最简答的一个模型了）

最优解问题的抽象具备了“0-1”特征（埋个伏笔，下面将会有大量与0-1有关的二进制dp系列问题哦o(￣┰￣*)ゞ） 代码上吧：

（很精简，没有给出具体注释，只有头注释，请读者不妨花点时间自己尽情感受一下吧(#｀-_ゝ-)(#｀-_ゝ-)好吧，比较懒而已）

/* 经典0-1背包DP问题 “0-1”抽象的递推特征与状态转移方程 递归设计与最优解问题（局部最优子结构）标记数组记录选择情况 */
#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

struct item {
	int value;
	int weight;
};

const int nmax = 100 + 5;
const int mmax = 10000 + 5;

int n, w;
item items[nmax];
int dp[nmax][mmax];
int g[nmax][mmax];

void compute(int &maxvalue, vector<int> &selection) {
	for (int i = 0; i <= w; i++) {
		dp[0][i] = 0;
		g[0][i] = 1;
	}
	for (int i = 0; i <= n; i++) {
		dp[i][0] = 0;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= w; j++) {
			dp[i][j] = dp[i - 1][j];
			g[i][j] = 0;
			if (items[i].weight > j)continue;
			if (items[i].value + dp[i - 1][j - items[i].weight] > dp[i - 1][j]) {
				dp[i][j] = items[i].value + dp[i - 1][j - items[i].weight];
				g[i][j] = 1;
			}
		}
	}
	maxvalue = dp[n][w];
	selection.clear();
	for (int i = n, j = w; i >= 1; i--) {
		if (g[i][j]) {
			selection.push_back(i);
			j -= items[i].weight;
		}
	}
	reverse(selection.begin(), selection.end());
}

int main() {
	cin >> n >> w;
	for (int i = 1; i <= n; i++) {
		int x, y;
		cin >> x >> y;
		items[i].value = x;
		items[i].weight = y;
	}
	memset(dp, 0, sizeof(dp));
	memset(g, 0, sizeof(g));
	int maxvalue;
	vector<int> selection;
	compute(maxvalue, selection);
	cout << maxvalue << endl;
	for (vector<int>::iterator it = selection.begin(); it != selection.end(); it++) {
		cout << *it << " ";
	}
	cout << "\\n";
	return 0;
}

 再来一道吧，应该有感觉了吧。

最大正方形，不多废话，一样的板子，直接来方程和代码：

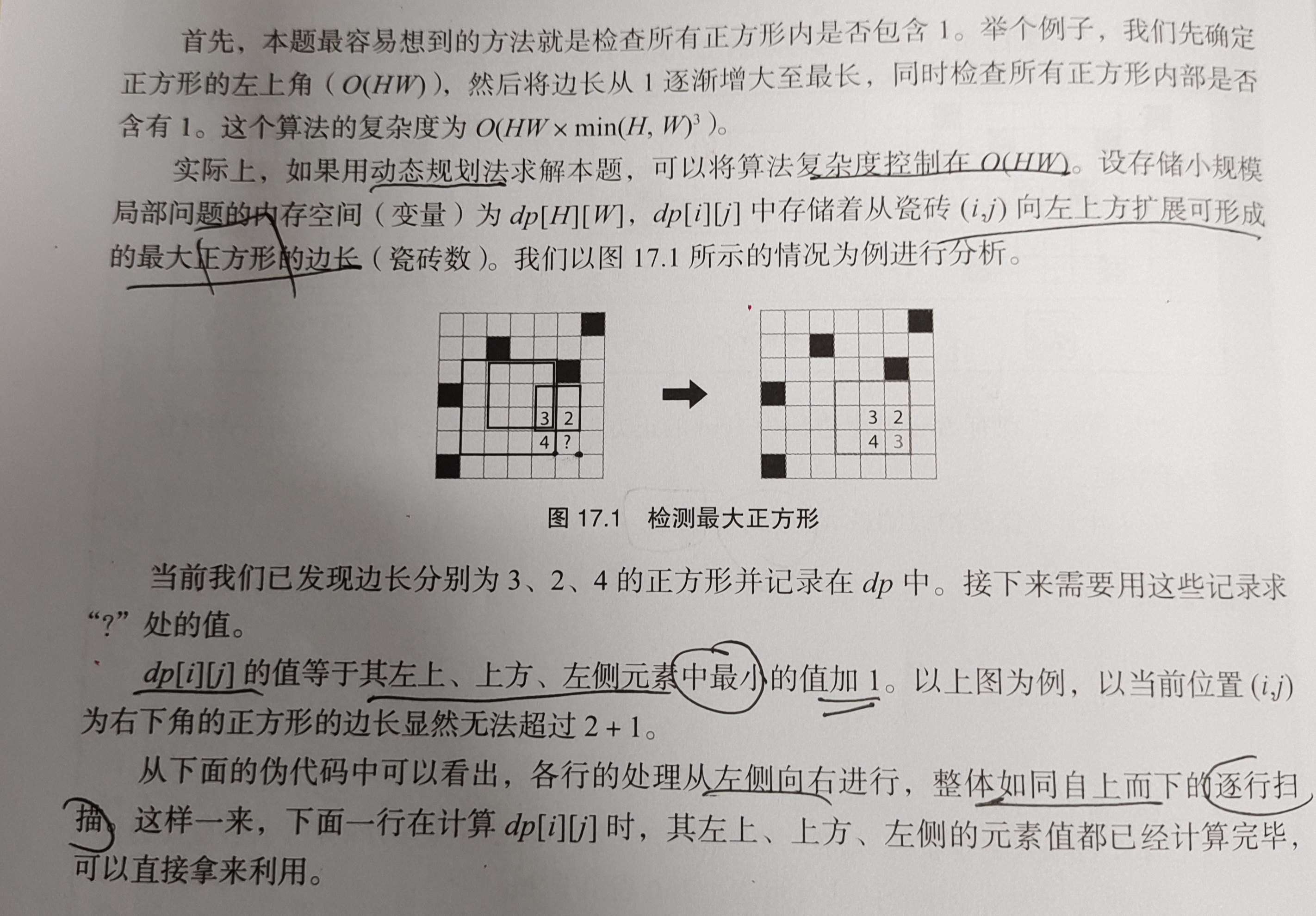
/* 最大正方形 动态规划的本质特征 状态转移 预处理 递归与分治 */
//a.动态规划：局部最优子结构 大问题分解位局部小问题 
//b.状态转移：某一步的状态可由或者仅由其前一步或者前几步推导 即可进行状态转移 可写出状态转移方程
//记忆化递归：有了a b的条件基础既可实现dp，记忆局部最优解，自底向上循环至整个最优解
#include <iostream>

using namespace std;

const int maxn = 1500;
int dp[maxn][maxn];
int graph[maxn][maxn];
int H, W;

int min(int x, int y, int z) {
	if (x < y) {
		if (x < z) return x;
		else return z;
	}
	else {
		if (y < z)return y;
		else return z;
	}
}

int max(int x, int y) {
	return (x > y ? x : y);
}

int getlargestsquare() {
	int maxwidth = 0;
	for (int i = 0; i < H; i++) {
		for (int j = 0; j < W; j++) {
			dp[i][j] = (graph[i][j] + 1) % 2;
			maxwidth |= dp[i][j];
		}
	}
	for (int i = 1; i < H; i++) {
		for (int j = 1; j < W; j++) {
			if (graph[i][j]) {
				dp[i][j] = 0;
			}
			else {
				dp[i][j] = min(dp[i - 1][j - 1], dp[i][j - 1], dp[i - 1][j]) + 1;
				maxwidth = max(maxwidth, dp[i][j]);
			}
		}
	}
	return maxwidth*maxwidth;
}

int main() {
	cin >> H >> W;
	for (int i = 0; i < H; i++) {
		for (int j = 0; j < W; j++) {
			cin >> graph[i][j];
		}
	}
	cout << getlargestsquare() << endl;
	return 0;
}

 （好了，基本动态规划就先到这吧，待会会继续补充一篇文章来记录状态压缩动态规划哦，也就是前面的伏笔啦（＞人＜；）。）