最长公共子序列（动态规划）

Posted 2021-04-18 Java编程生涯

一、简介

最长公共子序列简称LCS，表示两个或多个序列中最长的子序列。

本质：用来寻找两个或多个序列（字符串）中最长的子序列，而子序列又可能是不连续的。

描述：两个或多个序列的“相似度”

例如：

“BACD” 和 “CBDB” 中最长的子序列是“BD”

“AAABBBCCC” 和“DDAAFFEBBECC” 中最长的子序列是“AABBCC”

二、动态规划图解

“BACD”和“CBDB”相似度演示过程(填表)：

第一步：初始化一个二维数组表格

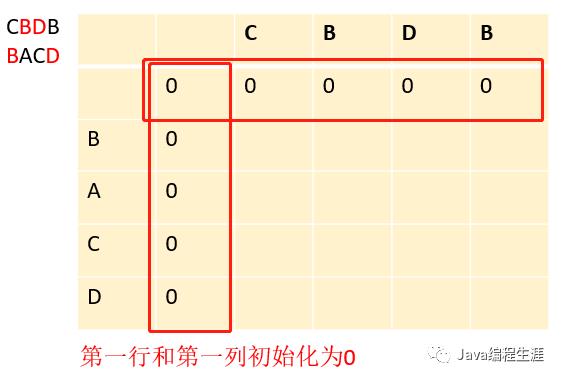
第二步：因为B和C不相等，取左方向或上方向较大的值

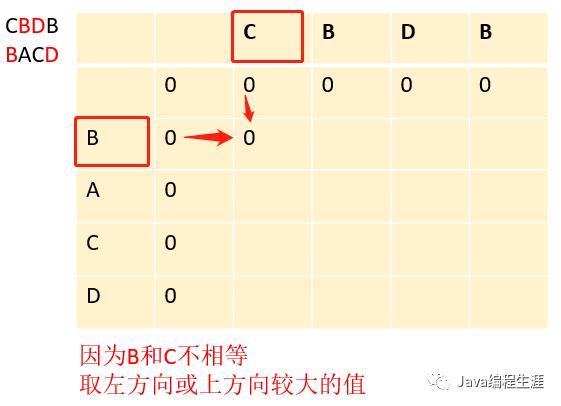
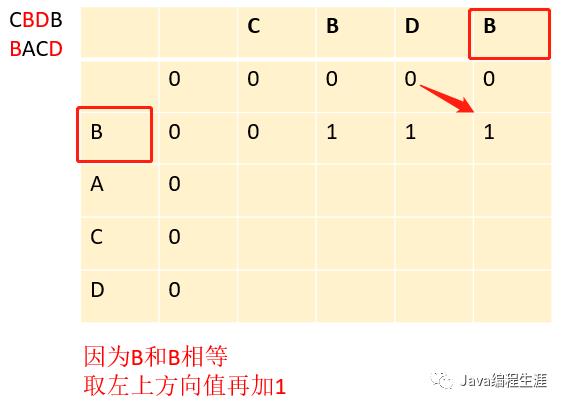
第三步：因为B和B相等，取左上方的值在加1

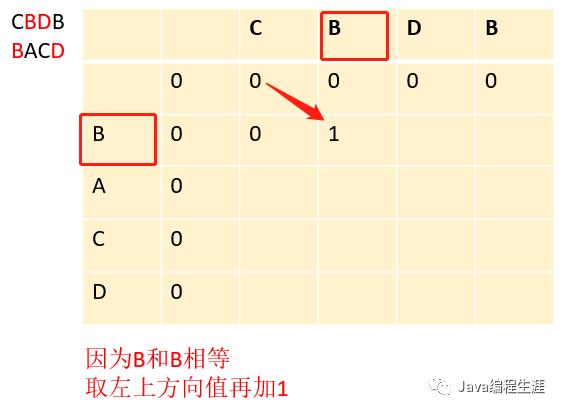
第四步：因为B和D不相等，取左方向或上方向较大的值

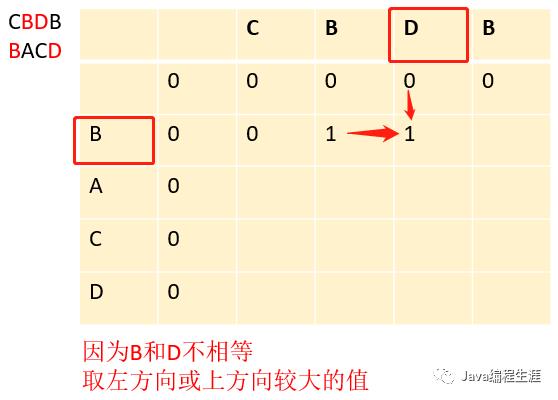
第五步：因为B和B相等，取左上方的值在加1

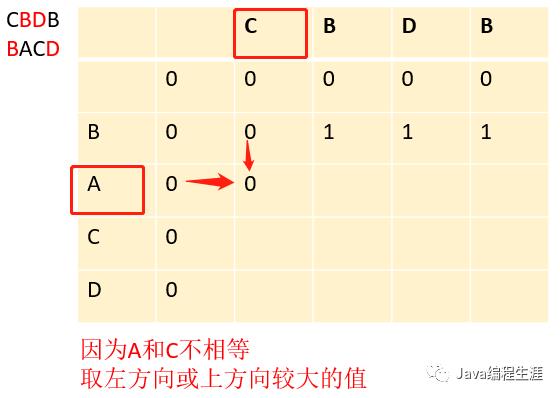
第六步：因为A和C不相等，取左方向或上方向较大的值

第七步：因为A和B不相等，取左方向或上方向较大的值

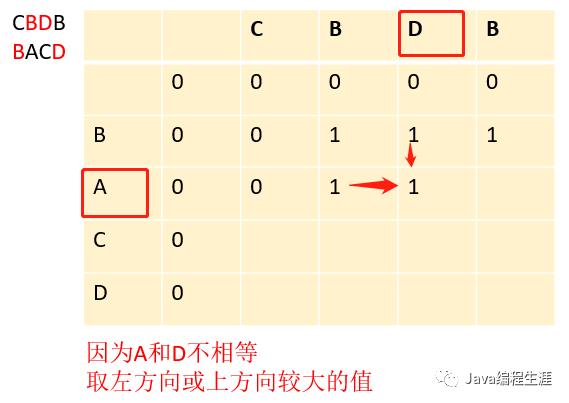
第八步：因为A和D不相等，取左方向或上方向较大的值

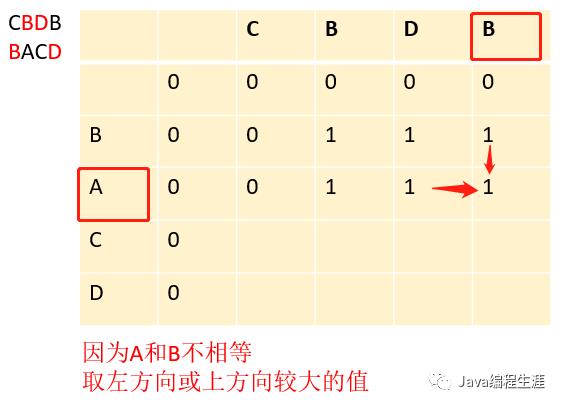
第九步：因为A和B不相等，取左方向或上方向较大的值

第十步：因为C和C相等，取左上方向值再加1

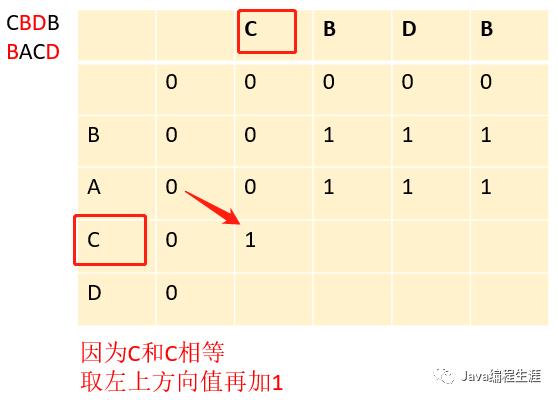
第十一步：因为C和B不相等，取左方向或上方向较大的值

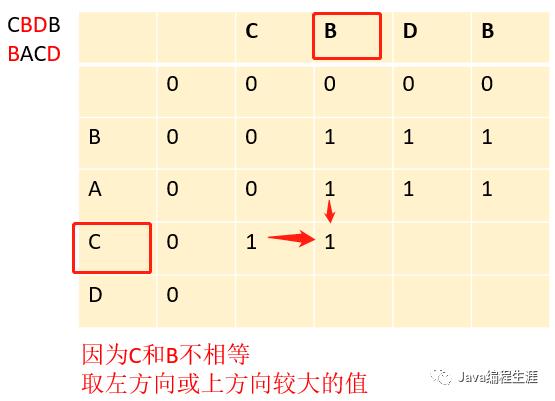
第十二步：因为C和D不相等，取左方向或上方向较大的值

第十三步：因为C和B不相等，取左方向或上方向较大的值

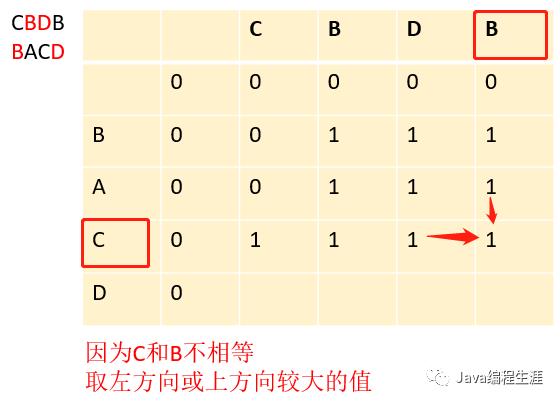
第十四步：因为D和C不相等，取左方向或上方向较大的值

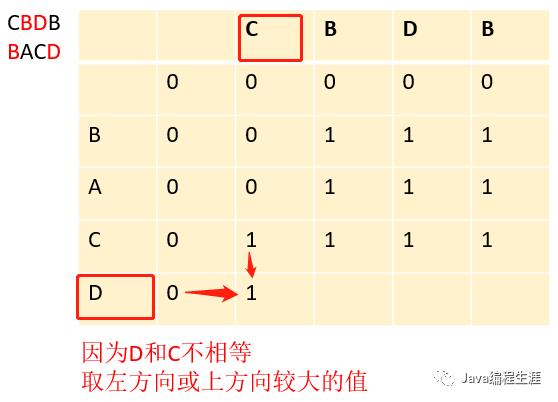
第十五步：因为D和B不相等，取左方向或上方向较大的值

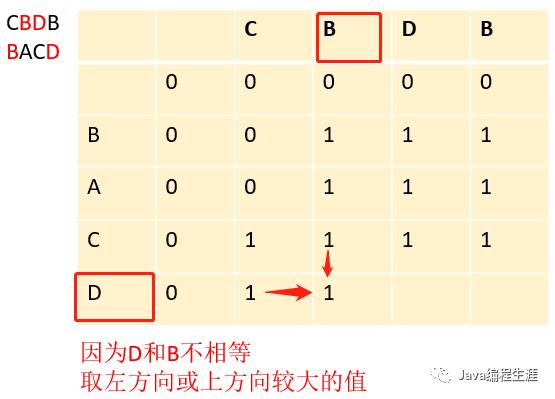
第十六步：因为D和D相等，取左上方向值再加1

第十七步：因为D和B不相等，取左方向或上方向较大的值

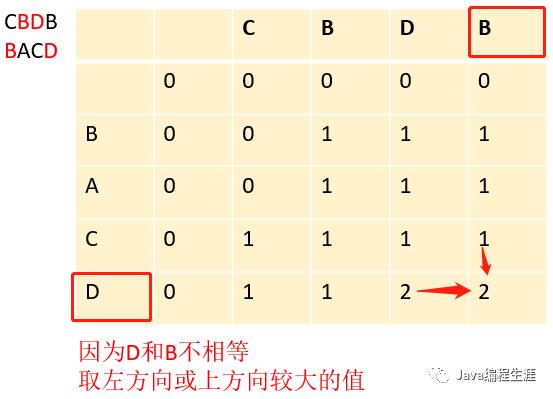
第十八步：由于已经填充完，最大的长度为2，“BACD”和“CBDB”相似度为2

三、动态规划

步骤：

第一步：先声明一个二维数组存储序列的长度。

第二步：再声明一个二维数组存储序列相同的字符。

第三步：从最后一个长度为2的位置，反向查找相同的字符。

第四步：把相同的字符拼接好，并反转之后再返回。

效果图：

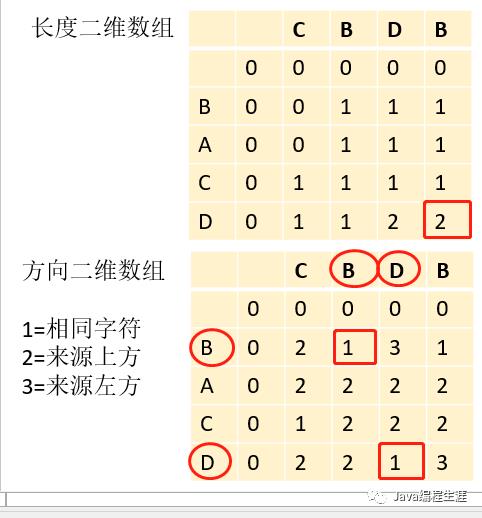
源码：

/**
 * 最长公共子序列
 * @param str1
 * @param str2
 * @return
 */
public static String lcs(String str1, String str2) {
    if (str1 == null || str2 == null) {
        return "";
    }

    char[] ch1 = str1.toCharArray();
    char[] ch2 = str2.toCharArray();

    int c1 = ch1.length + 1;
    int c2 = ch2.length + 1;

    int[][] array = new int[c1][c2]; // 存储最长公共子序列的长度
    int[][] direction = new int[c1][c2]; // 存储最长公共子序列长度方向的来源

    // 比较, 获取最长公共子序列的长度, 和长度方向的来源
    for (int i = 0; i < c1 - 1; i++) {
        for (int j = 0; j < c2 - 1; j++) {
            if (ch1[i] == ch2[j]) { // 两个相等,左上方的值加1

                array[i+1][j+1] = array[i][j]+1;
                direction[i+1][j+1] = 1; // 来源左上方，表示相同的字符
            } else {
                // 如果两个值不相等,判断上方和左方那个比较大,取较大的
                if (array[i][j+1] >= array[i+1][j]) {

                    array[i+1][j+1] = array[i][j+1];
                    direction[i+1][j+1] = 2; // 来源上方
                } else {

                    array[i+1][j+1] = array[i+1][j];
                    direction[i+1][j+1] = 3; // 来源左方
                }
            }
        }
    }

    // 拼接公共的字符
    StringBuilder builder = new StringBuilder();

    // 获取最长公共子序列相同的字符, 从最后一个字符开始
    int i = c1 - 1, j = c2-1;
    while (i >= 0 && j >= 0) {
        if (direction[i][j] == 1) {
            i--;
            j--;
            // 相同的字符
            builder.append(ch1[i]);
        } else if (direction[i][j] == 2) {
            i--;
        } else {
            j--;
        }
    }

    // 把字符串反转返回
    return (builder != null && builder.length() > 0) ? builder.reverse().toString() : "";
}

未

完

待

续

旧书不厌百回读，熟读精思子自知。

--苏轼