漫画：Go 讲解动态规划系列 第二讲

Posted 2021-04-18 Go语言中文网

在上一篇文章中，我们讲解了DP的概念并且通过示例了解了什么是动态规划。本篇中，我们将继续通过1道简单题型，进一步学习动态规划的思想。

0 1

第53题：最大子序和

第53题：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],

输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

拿到题目请不要看下方题解，先自行思考2-3分钟....

02

题目图解

首先我们分析题目，一个连续子数组一定要以一个数作为结尾，那么我们可以将状态定义成如下：

dp[i]：表示以 nums[i] 结尾的连续子数组的最大和。

那么为什么这么定义呢？因为这样定义其实是最容易想到的！在上一节中我们提到，状态转移方程其实是通过1-3个参数的方程来描述小规模问题和大规模问题间的关系。

当然，如果你没有想到，其实也非常正常！因为 "该问题最早于 1977 年提出，但是直到 1984 年才被发现了线性时间的最优解法。" 

根据状态的定义，我们继续进行分析：

如果要得到dp[i]，那么nums[i]一定会被选取。并且 dp[i] 所表示的连续子序列与 dp[i-1] 所表示的连续子序列很可能就差一个 nums[i] 。即 

dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)

但是这里我们遇到一个问题，很有可能dp[i-1]本身是一个负数。那这种情况的话，如果dp[i]通过dp[i-1]+nums[i]来推导，那么结果其实反而变小了，因为我们dp[i]要求的是最大和。所以在这种情况下，如果dp[i-1]<0，那么dp[i]其实就是nums[i]的值。即

dp[i] = nums[i] , if (dp[i-1] < 0)

综上分析，我们可以得到：

dp[i]=max(nums[i], dp[i−1]+nums[i])

得到了状态转移方程，但是我们还需要通过一个已有的状态的进行推导，我们可以想到 dp[0] 一定是以 nums[0] 进行结尾，所以 

dp[0] = nums[0]

在很多题目中，因为dp[i]本身就定义成了题目中的问题，所以dp[i]最终就是要的答案。但是这里状态中的定义，并不是题目中要的问题，不能直接返回最后的一个状态 (这一步经常有初学者会摔跟头)。所以最终的答案，其实我们是寻找：

max(dp[0], dp[1], ..., d[i-1], dp[i])

分析完毕，我们绘制成图：

假定 nums 为  [-2,1,-3,4,-1,2,1,-5,4]

03

Go语言示例

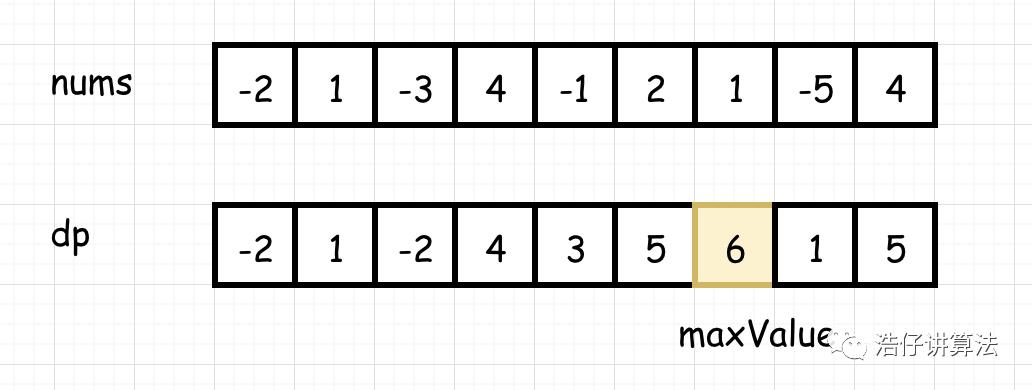
根据分析，得到代码：

 1func maxSubArray(nums []int) int {
 2    if len(nums) < 1 {
 3        return 0
 4    }
 5    dp := make([]int, len(nums))
 6    //设置初始化值 
 7    dp[0] = nums[0]
 8    for i := 1; i < len(nums); i++ {
 9        //处理 dp[i-1] < 0 的情况
10        if dp[i-1] < 0 {
11            dp[i] = nums[i]
12        } else {
13            dp[i] = dp[i-1] + nums[i]
14        }
15    }
16    result := -1 << 31
17    for _, k := range dp {
18        result = max(result, k)
19    }
20    return result
21}
22
23func max(a, b int) int {
24    if a > b {
25        return a
26    }
27    return b
28}

我们可以进一步精简代码为：

 1func maxSubArray(nums []int) int {
 2    if len(nums) < 1 {
 3        return 0
 4    }
 5    dp := make([]int, len(nums))
 6    result := nums[0]
 7    dp[0] = nums[0]
 8    for i := 1; i < len(nums); i++ {
 9        dp[i] = max(dp[i-1]+nums[i], nums[i])
10        result = max(dp[i], result)
11    }
12    return result
13}
14
15func max(a, b int) int {
16    if a > b {
17        return a
18    }
19    return b
20}

复杂度分析：时间复杂度：O(N)。空间复杂度：O(N)。

注：本系列所有教程中都不会用到复杂的语言特性，大家不需要担心没有学过go。算法思想最重要，使用go纯属本人爱好。同时，本系列所有代码均在leetcode上进行过测试运行，保证其严谨性！

推荐阅读

• 
  

---

喜欢本文的朋友，欢迎关注“Go语言中文网”：