文末福利算法萌新如何学好动态规划(第二弹)
Posted 力扣加加
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了文末福利算法萌新如何学好动态规划(第二弹)相关的知识,希望对你有一定的参考价值。
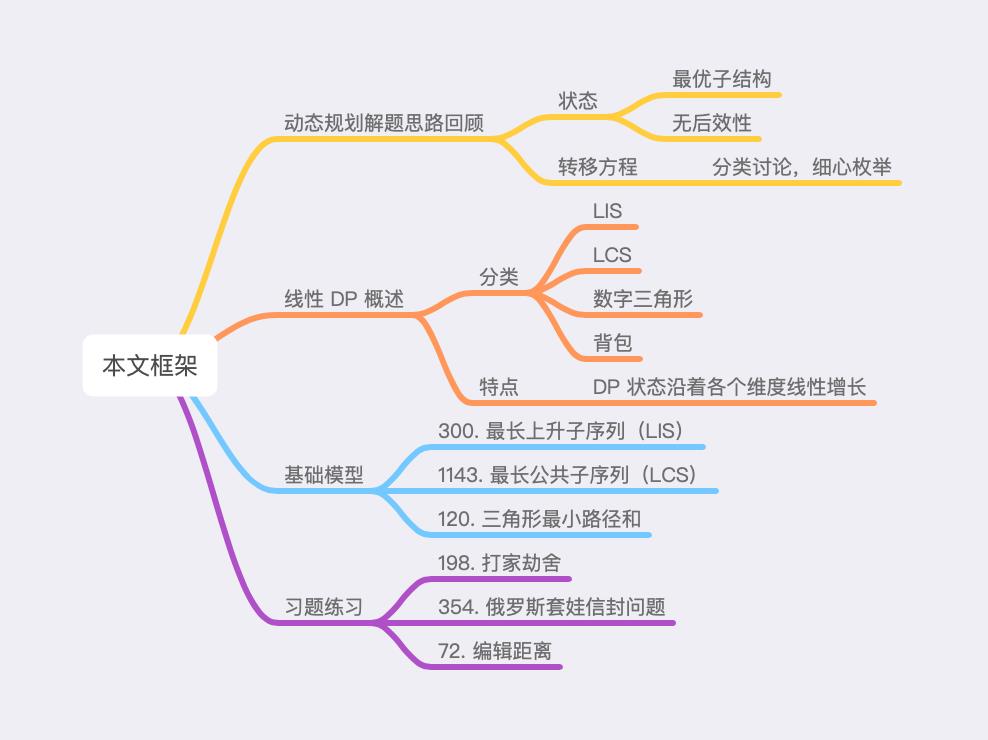

动态规划解题思路回顾
在正式开始线性 DP 的介绍前,我们需要回忆一下「」中的主要内容,即动态规划的解题思路。

线性 DP 概述
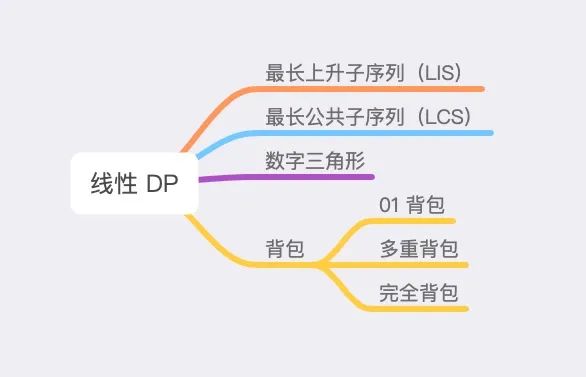

基础模型
300. 最长上升子序列(LIS)
题目描述
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例
输入: [10,9,2,5,3,7,101,18]输出: 4解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
模型讲解
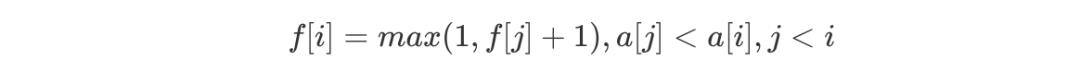
C++ 代码实现
class Solution {public:int lengthOfLIS(vector<int>& nums) {int sz = nums.size(), ans = 0;vector<int> f(sz, 0);for(int i = 0; i < sz; i++) {int tmp = 1;for(int j = i-1; j >= 0; j--) {if(nums[i] > nums[j])tmp = max(tmp, f[j]+1);}f[i] = tmp;ans = max(ans, tmp);}return ans;}};
1143. 最长公共子序列(LCS)
题目描述
示例 1
输入:text1 = "abcde", text2 = "ace"输出:3解释:最长公共子序列是 "ace",它的长度为 3。
示例 2
输入:text1 = "abc", text2 = "abc"输出:3解释:最长公共子序列是 "abc",它的长度为 3。
示例 3
输入:text1 = "abc", text2 = "def"输出:0解释:两个字符串没有公共子序列,返回 0。
提示

模型讲解
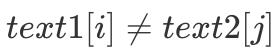 ,即 text1[i] 无法与 text2[j] 匹配,因此 f[i][j] = max(f[i][j - 1],f[i - 1][j])。
,即 text1[i] 无法与 text2[j] 匹配,因此 f[i][j] = max(f[i][j - 1],f[i - 1][j])。
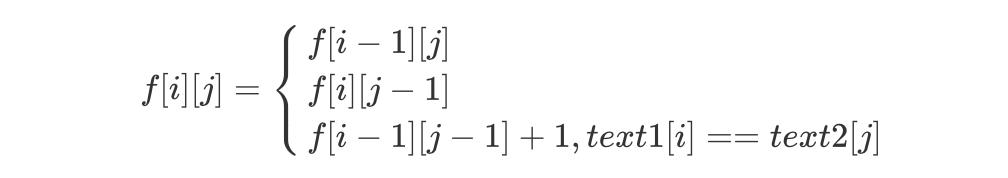
C++ 代码实现
class Solution {public:int longestCommonSubsequence(string text1, string text2) {int n = text1.length(), m = text2.length();vector<vector<int> > f(n+1, vector<int>(m+1, 0));for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {f[i][j] = max(f[i-1][j], f[i][j-1]);if(text1[i-1] == text2[j-1])f[i][j] = max(f[i][j], f[i-1][j-1]+1);}}return f[n][m];}};
120. 三角形最小路径和
题目描述
[[2],[3,4],[6,5,7],[4,1,8,3]]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明
模型讲解
由于题目中限制(i,j)只能由(i - 1,j - 1)和(i - 1,j)两个点到达,因此我们可以得到如下「DP 转移方程」:
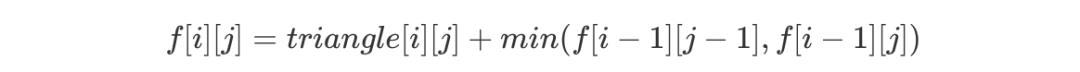
C++ 代码实现
class Solution {public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size(), ans = 1e9;vector<vector<int> > f(n+1, vector<int>(n+1, 0));for(int i = 0; i < n; i++) {for(int j = 0; j < triangle[i].size(); j++) {if(j == triangle[i].size()-1)f[i+1][j+1] = triangle[i][j] + f[i][j];else if(j == 0)f[i+1][j+1] = triangle[i][j] + f[i][j+1];elsef[i+1][j+1] = triangle[i][j] + min(f[i][j+1], f[i][j]);if(i == n-1)ans = min(ans, f[i+1][j+1]);}}return ans;}};
滚动数组优化
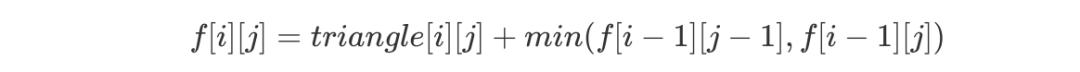
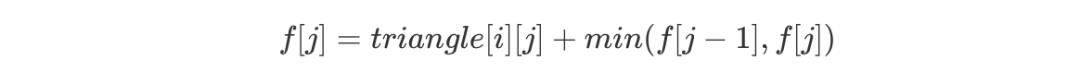
for(int i = 0; i < n; i++) {for(int j = triangle[i].size()-1; j >= 0; j--) {f[j] = triangle[i][j] + min(f[j-1], f[j]);}}
在上述代码中我们可以发现,在更新 f[j] 时,f[j - 1] 与 f[j] 并未更新,此时的 f[j - 1] 与 f[j] 其实是 f[i - 1][j - 1] 和 f[i - 1][j] 的值,因此这种转移方式正确。
滚动数组完整代码
class Solution {public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size(), ans = 1e9;vector<int> f(n+1, 0);for(int i = 0; i < n; i++) {for(int j = triangle[i].size()-1; j >= 0; j--) {if(j == triangle[i].size()-1)f[j+1] = triangle[i][j] + f[j];else if(j == 0)f[j+1] = triangle[i][j] + f[j+1];elsef[j+1] = triangle[i][j] + min(f[j+1], f[j]);if(i == n-1)ans = min(ans, f[j+1]);}}return ans;}};

习题练习
如何识别这是一道「线性 DP」问题
「DP 状态」是如何设置的
如何根据「DP 状态」得到「DP 转移方程」
题目描述
示例 1
输入:[1,2,3,1]输出:4解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2
输入:[2,7,9,3,1]输出:12解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示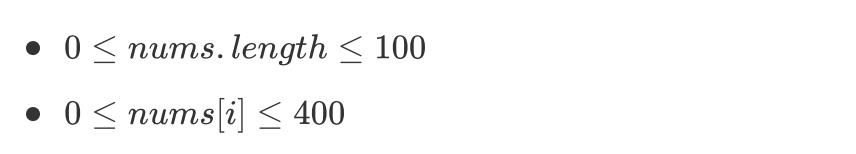
解题思路
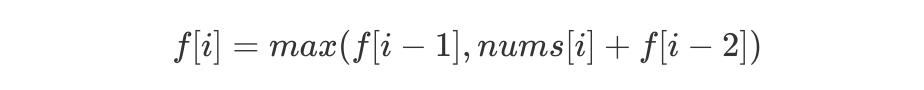
C++ 代码实现
class Solution {public:int rob(vector<int>& nums) {int n = nums.size();if(n == 0) return 0;vector<int> f(n, 0);for(int i = 0; i < n; i++) {f[i] = nums[i];if(i >= 2) f[i] = max(f[i], f[i-2]+nums[i]);if(i >= 1) f[i] = max(f[i], f[i-1]);}return f[n-1];}};
题目描述
说明
示例
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]输出: 3解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
解题思路
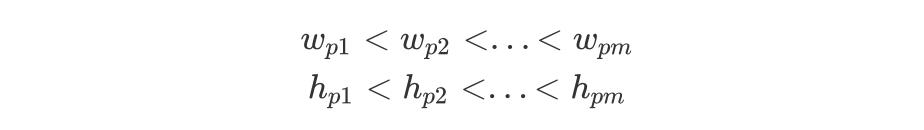
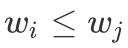 ,因此我们可以先对于信封进行排序,w 为第一关键字,h 为第二关键字,排完序后再进行初始的一维 LIS「DP 转移」。
,因此我们可以先对于信封进行排序,w 为第一关键字,h 为第二关键字,排完序后再进行初始的一维 LIS「DP 转移」。
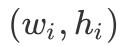 为结尾的最长上升子序列,「DP 转移方程」如下:
为结尾的最长上升子序列,「DP 转移方程」如下:
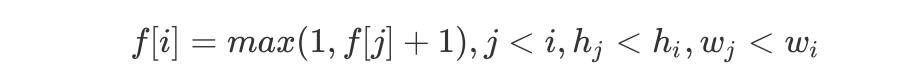
C++ 代码实现
class Solution {public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end());int n = envelopes.size(), ans = 0;vector<int> f(n, 0);for(int i = 0; i < n; i++) {int tmp = 0;for(int j = 0; j < i; j++) {if(envelopes[j][1] < envelopes[i][1] && envelopes[j][0] < envelopes[i][0])tmp = max(tmp, f[j]);}f[i] = tmp + 1;ans = max(f[i], ans);}return ans;}};
题目描述
插入一个字符
删除一个字符
替换一个字符
示例 1
输入:word1 = "horse", word2 = "ros"输出:3解释:horse -> rorse (将 'h' 替换为 'r')rorse -> rose (删除 'r')rose -> ros (删除 'e')
示例 2
输入:word1 = "intention", word2 = "execution"输出:5解释:intention -> inention (删除 't')inention -> enention (将 'i' 替换为 'e')enention -> exention (将 'n' 替换为 'x')exention -> exection (将 'n' 替换为 'c')exection -> execution (插入 'u')
解题思路
与 LCS 的思考过程一致,假如 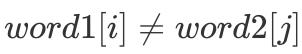 ,则必定涉及删除或增加:
,则必定涉及删除或增加:
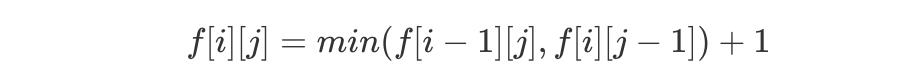
假如 word1[i] == word2[j],则需要在原先基础上增加一种转移方式:
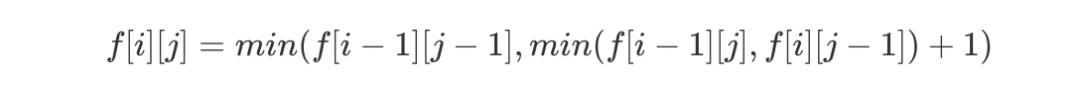
最后我们需要控制一下边界:
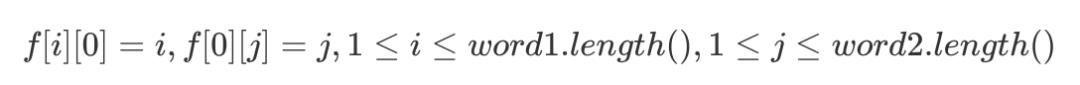
C++ 代码实现
class Solution {public:int minDistance(string word1, string word2) {int n = word1.length(), m = word2.length();vector<vector<int> > f(n+1, vector<int>(m+1, 0));for(int i = 1; i <= n; i++) f[i][0] = i;for(int j = 1; j <= m; j++) f[0][j] = j;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(word1[i-1] == word2[j-1]) f[i][j] = f[i-1][j-1];else f[i][j] = min(f[i-1][j-1]+1, min(f[i][j-1]+1, f[i-1][j]+1));}}return f[n][m];}};

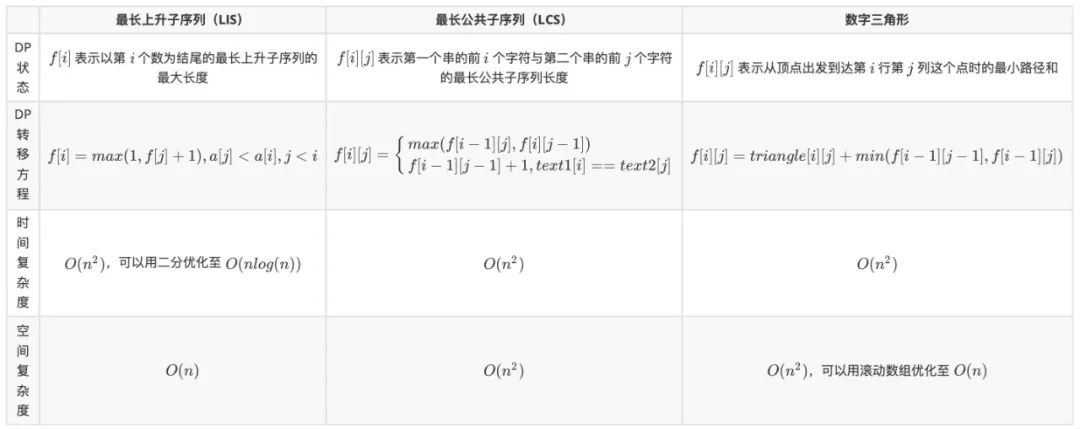
总结
小漾
以上是关于文末福利算法萌新如何学好动态规划(第二弹)的主要内容,如果未能解决你的问题,请参考以下文章