开发者说丨使用动态规划实现正则表达式匹配

Posted 2021-04-18 Apollo开发者社区

动态规划的英文为：Dynamic Programming，这里的“Programming”并非指编写程序代码，而是指一种表格计算法（A tabular method），即基于表格查询的方法计算得到最优结果。

本文由社区荣誉布道师——贺志国撰写，对使用动态规划实现正则表达式匹配进行了详细讲解，希望这篇文章能给感兴趣的开发者带来更多帮助。

  以下，ENJOY  

给定一个字符串 s 和一个字符串模式 p，请你来实现一个支持 . 和 * 的正则表达式匹配。

1. . 匹配任意单个字符。

2. * 匹配零个或多个前面的那一个元素。

所谓匹配，是要涵盖整个字符串 p，而不是部分字符串。

说明：

1. s 可能为空，且只包含从 a-z 的小写字母。

2. p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 * 。

 

示例1：

1输入:
2s = "aa"
3p = "a"
4输出: 
5false
6解释: 
7"a" 无法匹配 "aa" 整个字符串。

<左右滑动以查看完整代码>

示例2：

1输入:
2s = "aa"
3p = "a*"
4输出: 
5true
6解释: 
7因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。
8因此，字符串 "aa" 可被视为 'a' 重复了一次。

<左右滑动以查看完整代码>

示例3：

 

1输入:
2s = "ab"
3p = ".*"
4输出: 
5true
6解释: 
7".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。
8首先，".*"匹配'a'，接下来".*"匹配' b'。

<左右滑动以查看完整代码>

示例4：

1输入:
2s = "aab"
3p = "c*a*b"
4输出: 
5true
6解释: 
7因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

<左右滑动以查看完整代码>

示例5：

1输入:
2s = "mississippi"
3p = "mis*is*p*."
4输出: 
5false
6解释: 
7因为 '*' 表示零个或多个，'s*p'不能匹配'ssip' 。

<左右滑动以查看完整代码>

动态规划与分治法（the divide-and-conquer method）有些类似，也是将问题分解为多个子问题，并且基于子问题的结果获得最终解。二者的区别是，分治法将初始问题划分为多个不关联（disjoint）的子问题（subproblem)（即子问题互不依赖），递归地解决子问题，然后将子问题的解合并得到初始问题的解。与之相反，动态规划法分解得到的子问题是相互重叠的（overlap），即子问题依赖于子子问题（subsubproblem)，子子问题又进一步依赖于下一级的子子问题，这样不断循环直至抵达不需分解的初始条件。在求解过程中，为了避免重复计算子子问题从而提高算法效率，需要将一系列子子问题的解保存到一张表中（table，C++编程一般使用std::array、std::vector 或std::list 实现），这也就是动态规划又被称为查表计算法的原因。

动态规划一般应用于最优化问题（optimization problems）。这类问题一般存在多个解，每个解都具有一个度量值，我们期望得到具有度量值最优（即取最大或最小值）的解。该最优解一般称为最优化问题的一个解。注意，这个解并非唯一，因为最优化问题可能存在多个最优解。

构建一个动态规划算法的一般步骤如下：

1. 刻画出一个最优解的结构特征（即使用数学表达式来表述一个最优解）；

2. 迭代定义一个最优解的度量值；

3. 计算每个最优解的度量值，通常采用自下而上的方式；

4. 根据计算得到的信息构建出原问题的一个最优解。

步骤1-3是使用动态规划求解问题的基础形式。如果我们只需获得最优解的度量值而非最优解本身，则可以忽略步骤4。

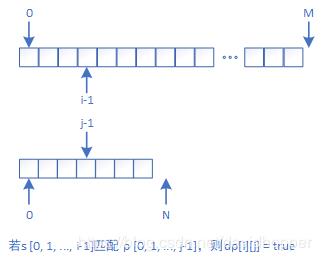
如上图所示，令字符串 s 的长度为 M ，字符串模式 p 的长度为 N 。如果s[0,1,...,i-1]与p[0,1,...,j-1]匹配，则令dp[i][j]=true 。根据上述定义，可得：dp[0][0]=true表示空字符串完全匹配空字符串，dp[1][1]=true表示p[0]完全匹配 s[0] ，dp[M][N]=true表示 p 完全匹配 s。

现在的任务是使用动态规划思想求解迭代表达式dp[i][j]（即s[0,1,...,i-1]与p[0,1,...,j-1]的匹配情况），下面分别阐述之：

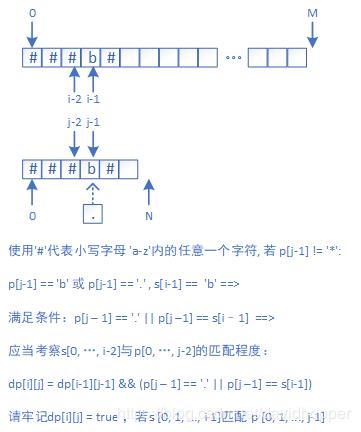
如上图所示，若p[j-1]!='*'，则p[j-1]要么是a-z的小写字母中的任意一个，要么是 . ，于是可得迭代表达式：

1 dp[i][j] = && dp[i - 1][j - 1] && (s[i - 1] == p[j - 1] || p[j - 1] == '.')

<左右滑动以查看完整代码>

说明：要求i>0&&i<=m&&j>0&&j<=N，以确保dp[i][j]与dp[i-1][j-1]取值不越界（下同，不再赘述）。

举例：s[0,...,i-1]='abc'，p[0,...,j-1]='abc'或p[0,...,j-1]='ab.'，可满足上述条件。

若p[j-1]=='*'，分为两种情况：

1.  p[j-2]==s[i-1]或p[j-2]=='.'

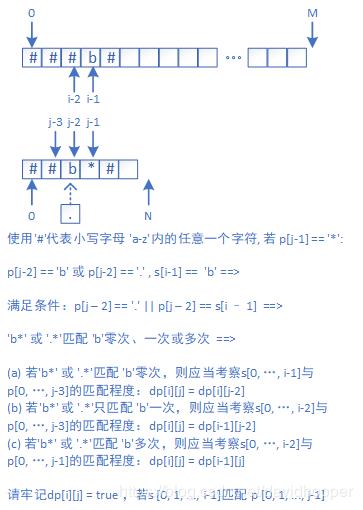
如上图所示，迭代表达式为：

1dp[i][j] = dp[i][j-2] || dp[i - 1][j - 2] || dp[i - 1][j], if p[j – 2] == s[i – 1] || p[j – 2] == '.'

<左右滑动以查看完整代码>

举例：p[0,...,j-1]='abc*'或p[0,...,j-1]='ab.*'可匹配s[0,...,i-1]='abc'（匹配 c 零次），s[0,...,i-1]='abcc'（匹配 c 一次）, s[0,...,i-1]='abcccc'（匹配 c 多次）。

2.  p[j-2]!=s[i-1]且P[j-2]!='.'

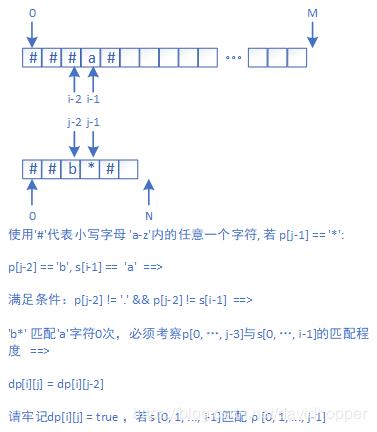
如上图所示，迭代表达式为：

1dp[i][j] = dp[i][j-2], if p[j-2] != '.' && p[j-2] != s[i-1] 

<左右滑动以查看完整代码>

举例：p[0,...,j-1]='abc*'可匹配s[0,...,i-1]='ab'。

综上所述，得到最终的迭代表达式如下：

1(1) if p[j - 1] != '*': 
2dp[i][j] = dp[i - 1][j - 1] && (s[i - 1] == p[j - 1] || p[j - 1] == '.'), 
3(2) if p[j - 1] == '*': 
4dp[i][j] = dp[i][j - 2] || ((p[j - 2] == '.' || p[j - 2] == s[i - 1])  &&  
5       (dp[i - 1][j - 2] || dp[i - 1][j]))  

<左右滑动以查看完整代码>

使用C++11实现，代码如下：

 1#include  
       
 2#include  
       
 3#include  
       
 4
 5class Solution {
 6public:
 7bool IsMatch(const std::string& s, const std::string& p) {
 8int m = s.size(), n = p.size();
 9std::vector<std::vector<bool>> dp(m + 1, std::vector<bool>(n + 1, false));
10dp[0][0] = true;
11for (int i = 0; i <= m; ++i) {
12  for (int j = 1; j <= n; ++j) {
13    // The first character shouldn't be '*'
14    if (j > 1 && p[j - 1] == '*') {
15      dp[i][j] = dp[i][j - 2] ||
16                 (i > 0 && (p[j - 2] == '.' || p[j - 2] == s[i - 1]) &&
17                  (dp[i - 1][j - 2] || dp[i - 1][j]));
18    } else {
19      dp[i][j] = i > 0 && dp[i - 1][j - 1] &&
20                 (s[i - 1] == p[j - 1] || p[j - 1] == '.');
21    }
22  }
23}
24return dp[m][n];
25}
26};
27
28int main() {
29std::string s1 = "aa";
30std::string p1 = "a";
31std::string s2 = "aa";
32std::string p2 = "a*";
33std::string s3 = "ab";
34std::string p3 = ".*";
35std::string s4 = "aab";
36std::string p4 = "c*a*b";
37std::string s5 = "mississippi";
38std::string p5 = "mis*is*p*.";
39std::string s6 = "test";
40std::string p6 = "*.";
41std::string s7 = "mississippi";
42std::string p7 = "mis*is*ip*.";
43
44Solution solution;
45std::cout << "Expected: 
false, true, true, true, false, false, true"
46        << std::endl;
47std::cout << "Actual: 
"
48        << std::boolalpha << solution.IsMatch(s1, p1) << ", "
49        << solution.IsMatch(s2, p2) << ", " << solution.IsMatch(s3, p3)
50        << ", " << solution.IsMatch(s4, p4) << ", "
51        << solution.IsMatch(s5, p5) << ", " << solution.IsMatch(s6, p6)
52        << ", " << solution.IsMatch(s7, p7) << std::endl;
53
54return 0;
55}

<左右滑动以查看完整代码>

输出结果：

1Expected: 
2false, true, true, true, false, false, true
3Actual: 
4false, true, true, true, false, false, true 

<左右滑动以查看完整代码>

以上是"使用动态规划实现正则表达式匹配"的全部内容，更多话题讨论、技术交流可以扫描下方二维码添加『Apollo小哥哥』为好友，进开发者交流群。

* 以上内容为开发者原创，不代表百度官方言论。

内容来自开发者CSDN：