动态规划之正则表达式匹配字符串
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划之正则表达式匹配字符串相关的知识,希望对你有一定的参考价值。
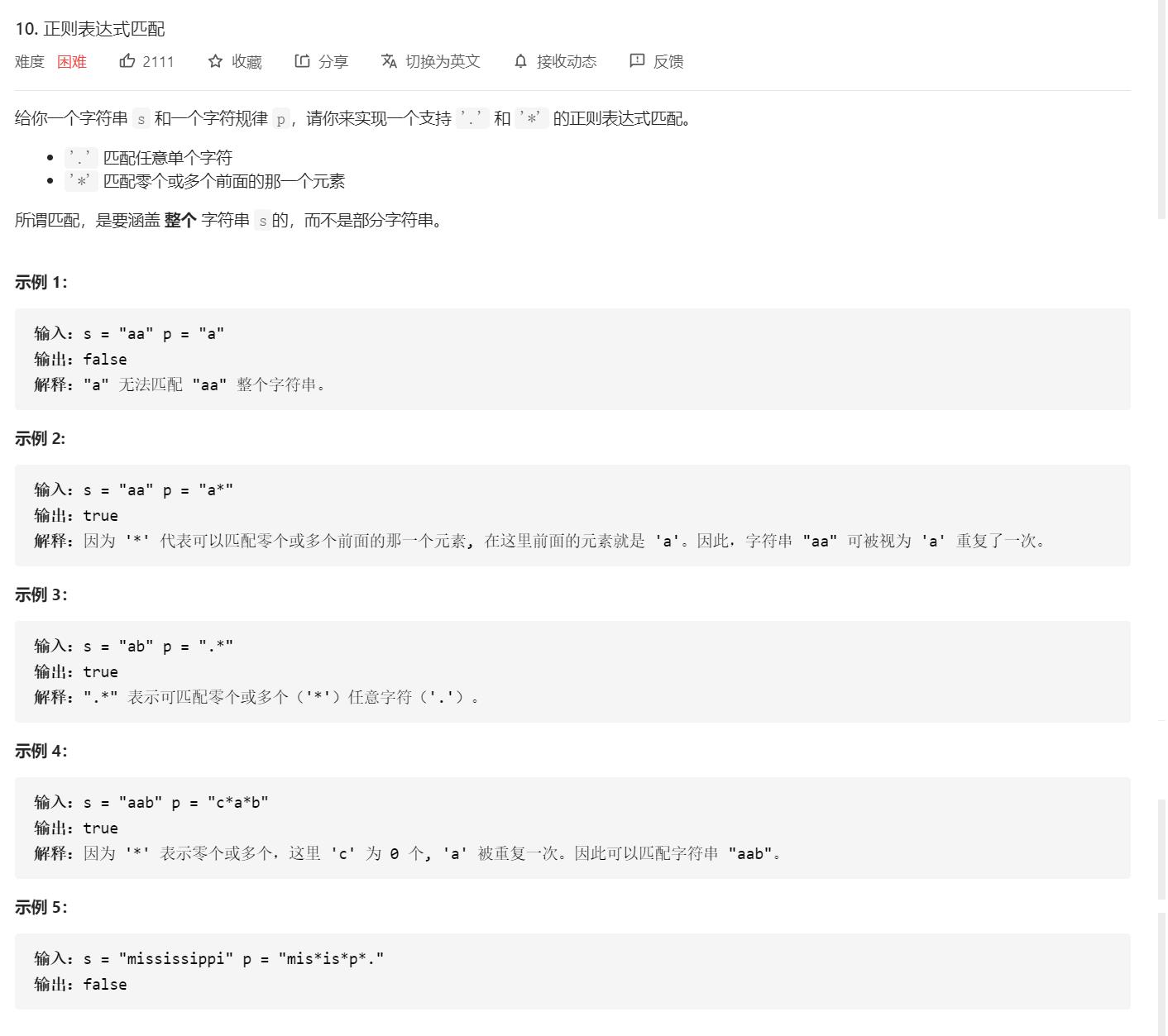
题目
解题思路
正则表达式的匹配规则我在这里就不多说了,相信大家都很清楚。
本题会给出两个字符串s和p,p代表的是模式串,也就是带有正则表达式的那个字符串,判断p是否可以匹配字符串s
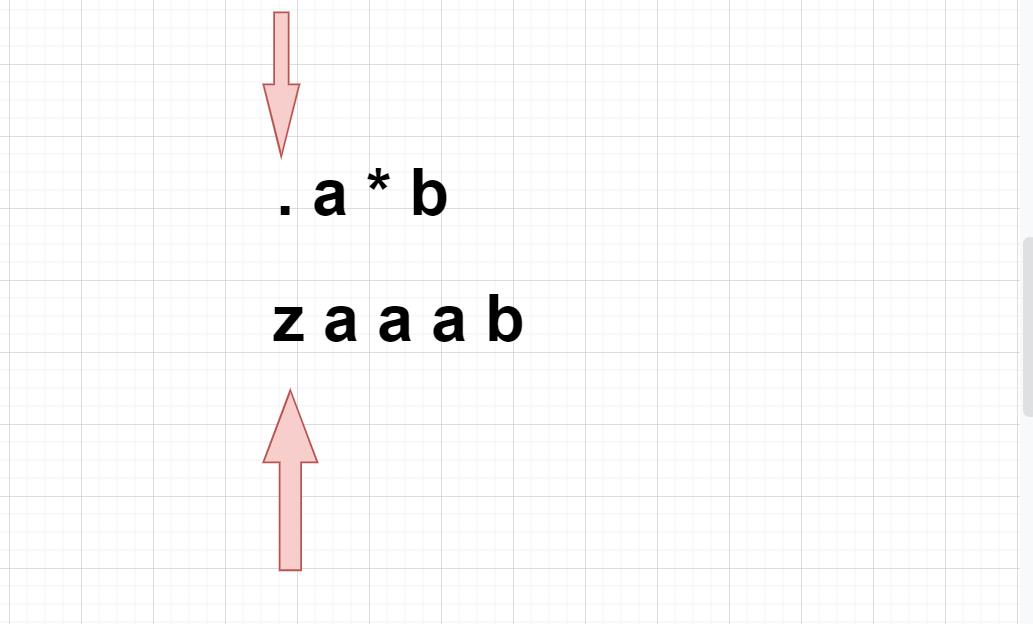
.号很好实现,遇到它直接匹配就可。难点就在于*,因为一旦出现 *号,它前面的字符可以出现1次,也可以出现n次,也可以不出现。比如.a*b就可以匹配zaaab
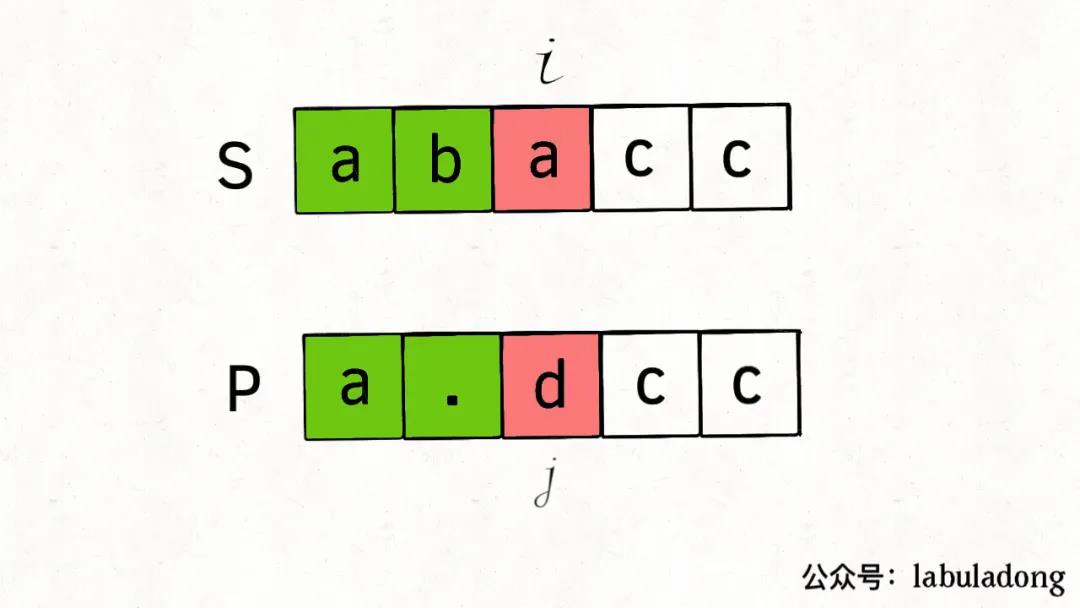
关于字符串的撇匹配,大家首先想到的肯定是两个指针:i和j分别在s和p上移动,如果他们都能移动到各自的字符串末尾,则匹配成功,否则失败
所以如果我们先不要考虑*,代码就能很容易写出来
bool isMatch(string s,string p)
{
int i,j=0;
while(i<s.size() && j<p.size())
{
if(s[j]==s[j] || p[j]=='.')
{
i++;
j++;
}
else
return false;
}
return true;
}
如果p[j+1]为通配符*,则考虑的情况较多,主要分为以下两种
1:如果s[i]==p[j],那么
p[j]有可能匹配多个字符,比如当s="aaa",p="a*"时,就匹配了3次p[j]也有可能匹配0个字符,比如当s="aa",p="a*aa",可以发现匹配了0次
2:如果s[i]!=p[j],那么
p[j]只能匹配0次,然后看p的下一个字符是否能和s[i]匹配。比如s="aa",p="b*aa"
于是我们可以写出伪代码如下
if(s[i]==p[j] || p[j]=='.')
{
if(j<p.size()-1 && p[j+1]=='*')
{
//有通配符*可以匹配0次或多次
}
else
{
//没有通配符*只能匹配1次
i++;
j++;
}
}
else
{
if(j<p.size()-1 && p[j+1]=='*')
{
//有通配符*可以,只能匹配0次
}
else
{
//没有通配符直接失败
return false;
}
}
代码的思路很清晰了,看起来的确很简单,那么为什么这道题难度还是hard呢?其实问题就在于*应该匹配0次还是多次 。那么既然属于动态规划的题目,因此这个问题就需要用到咋们之前讲到过的思想来解决了。
- 状态是什么?自然是i和j的位置
- 选择是什么?自然就是
p[j],也即是*应该匹配几个字符
动态规划
根据以上描述,首先按照暴力解法思想,先定义一个dp函数,如下
bool dp(string& s,int i,string& p,int j)
如果该函数返回值为true,表示可以匹配,反之不可以
bool isMathch(string s,string p)
{
return dp(s,0,p,0);
}
bool dp(string& s,int i,string& p,int j)
{
if(s[i]==p[j] || p[j]=='.')
{
if(j<p.size()-1 && p[j+1]=='*')
{
//1:可以匹配0次,或者多次
return dp(s,i,p,j+2) || dp(s,i+1,p,j);
}
else
{
//:2:只能匹配1次
return dp(s,i+1,p,j+1);
}
}
else
{
if(j<p.size()-1 && p[j+1]=='*')
{
//3:只能匹配0次,看下面有没有相等的
return dp(s,i,p,j+2);
}
else
{
//4:无法匹配
return false;
}
}
}
上述代码中,注释中的解释分别如下
1:可以匹配0次,或者多次:return dp(s,i,p,j+2) || dp(s,i+1,p,j)
-
j+2,i不变就是直接跳过p[j]和后面的通配符,即匹配了0次
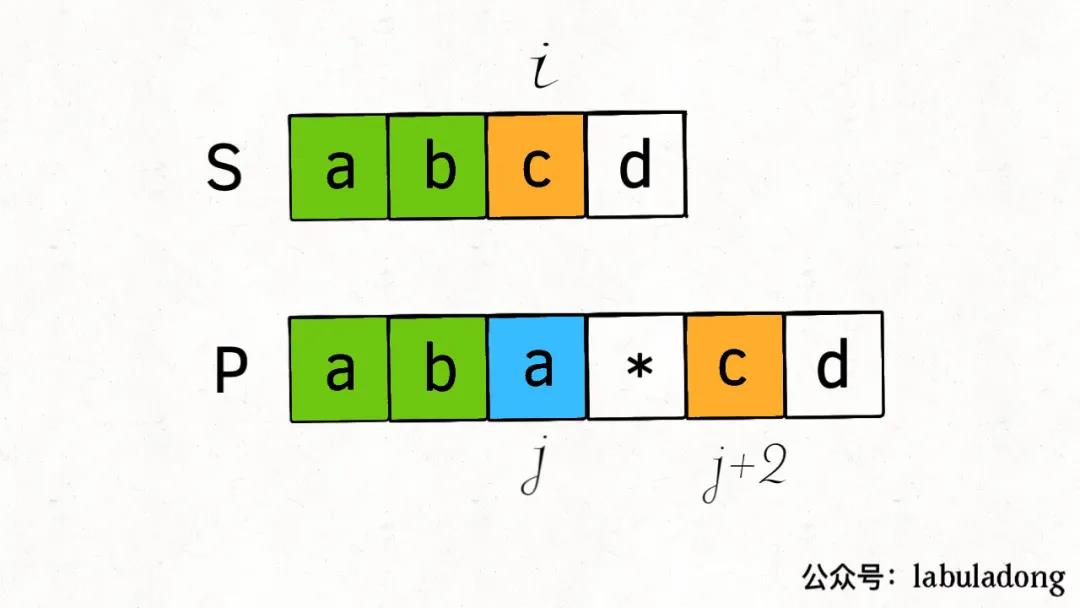
-
i+1,j不变,就是p[j]已经匹配了s[i],但是p[j]还可以匹配s[i]后面的,也就是匹配多次
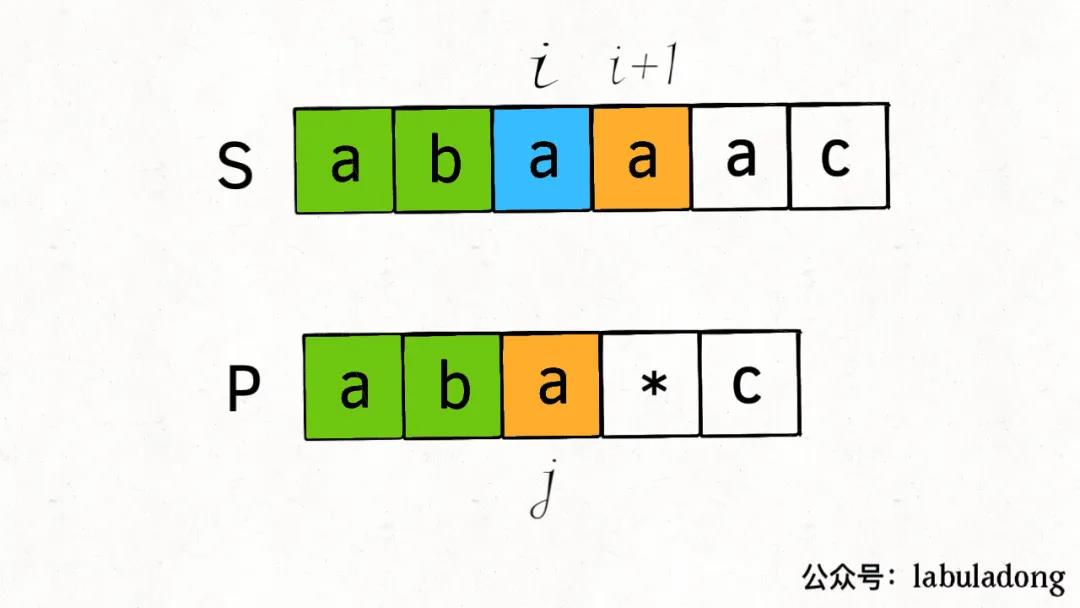
2:只能匹配1次:return dp(s,i+1,p,j+1),这种情况就不多做解释了
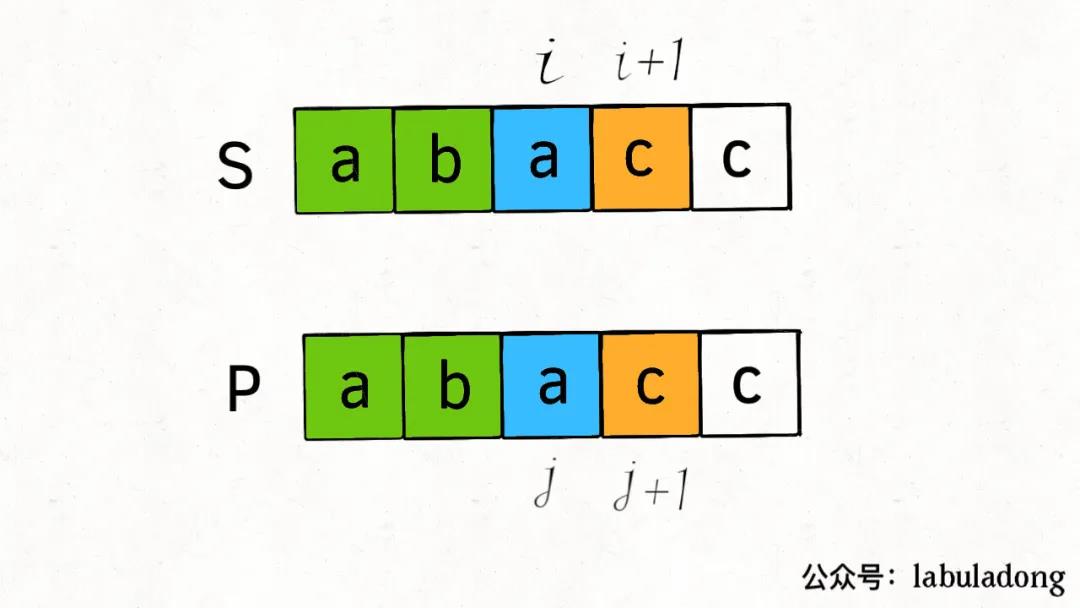
3:只能匹配0次,看下面有没有相等的:return dp(s,i,p,j+2)
- 这种情况和情况1中的第一种类似,也就是匹配0次
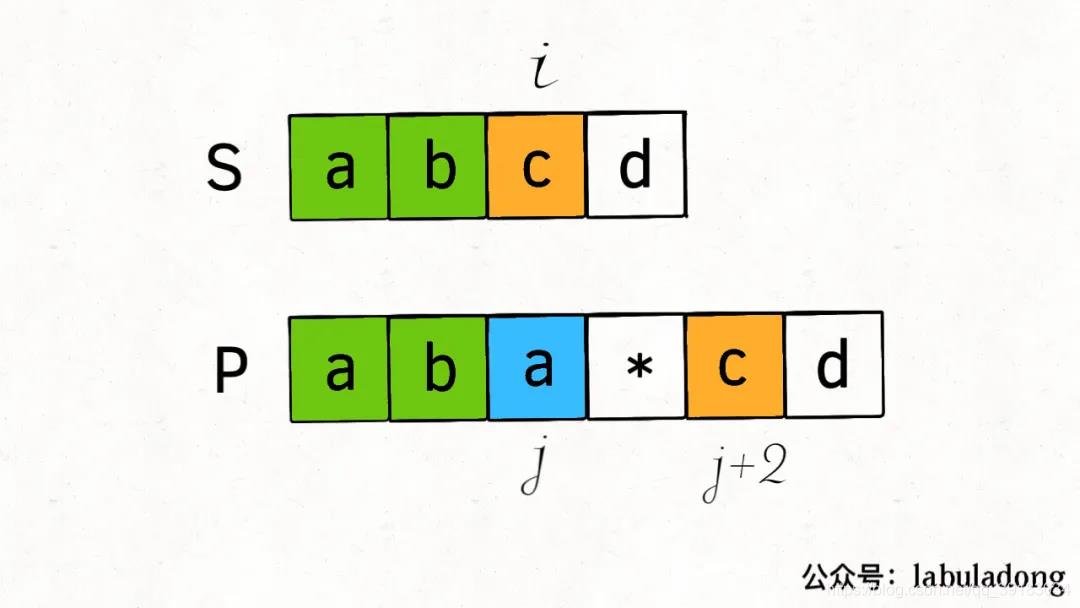
4:最后一种情况就是失败
最后需要处理一个棘手的问题,就是base case,因为base case决定了程序何时退出,以及退出的结果是否正确。
- 如果
j==p.size(),也就是p串走完,那么此时如果i也等于s.size(),就表示匹配成功 - 但是如果
i=p.size(),是不能通过判断是否j==p.size()的方式来判断是否成功的。因为可能会出现s="a",p=“ab*c*”这种情况,可以发现虽然p没有走完,但是它仍然是匹配的。
所以我们的思路是,首先if(j==p.size()),那么就return i==s.size(),如果此时i还等于s.size(),一定成功。
另一个重点就是i==size()时,去除掉一些干扰情况
- 如果
i==size(),那么对于p来说,其中的字符和*一定是成对出现的
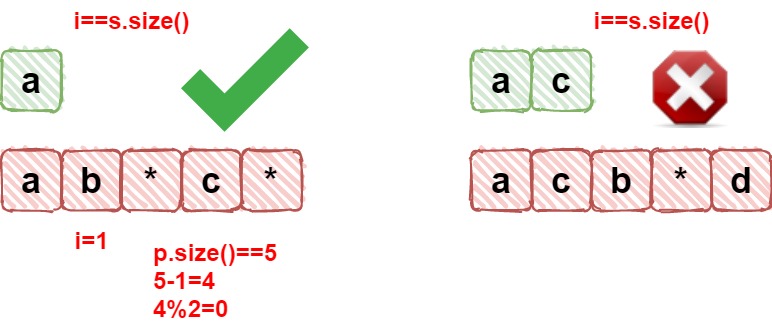
- 上面成对出现有一种非常奇葩的情况,就是通配符出现字母前,这样是无法匹配的,因此要把这种情况给剔除掉
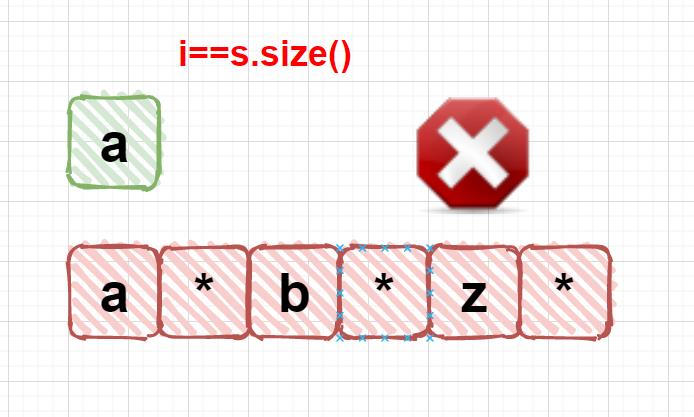
判断的代码如下
if(i==s.size())
{
if(p.size()-j)%2!=0)
{
return false;
}
for(;j<p.size();j+=2)
{
if(p[j+1]!='*')
{
return false;
}
}
return true;
}
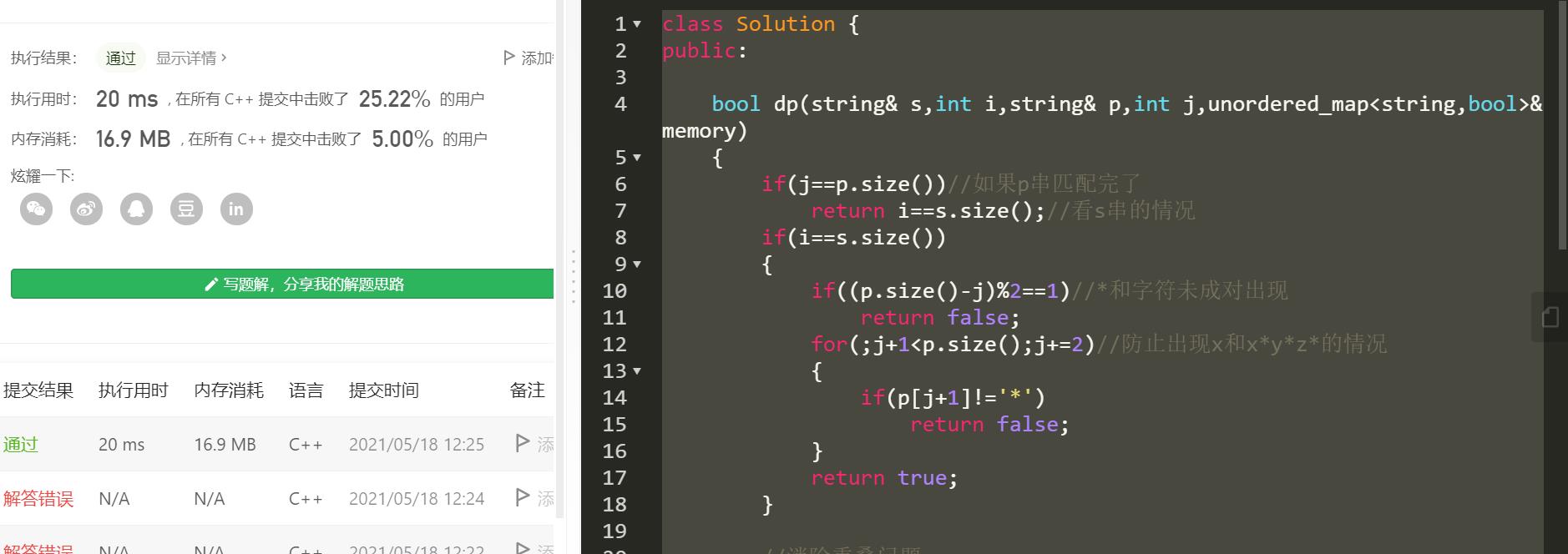
CODE
至此我们就可以写出完整的代码了
class Solution {
public:
bool dp(string& s,int i,string& p,int j,unordered_map<string,bool>& memory)
{
if(j==p.size())//如果p串匹配完了
return i==s.size();//看s串的情况
if(i==s.size())
{
if((p.size()-j)%2==1)//*和字符未成对出现
return false;
for(;j+1<p.size();j+=2)//防止出现x和x*y*z*的情况
{
if(p[j+1]!='*')
return false;
}
return true;
}
//消除重叠问题
string key=to_string(i)+","+to_string(j);
if(memory.count(key))
return memory[key];
bool res=false;
if(s[i]==p[j] || p[j]=='.')
{
if(j<p.size()-1 && p[j+1]=='*')
{
res=dp(s,i,p,j+2,memory) || dp(s,i+1,p,j,memory);
}
else
{
res=dp(s,i+1,p,j+1,memory);
}
}
else
{
if(j<p.size()-1 && p[j+1]=='*')
{
res=dp(s,i,p,j+2,memory);
}
else
{
res=false;
}
}
memory[key]=res;
return res;
}
bool isMatch(string s, string p)
{
unordered_map<string,bool> memory;
return dp(s,0,p,0,memory);
}
};
以上是关于动态规划之正则表达式匹配字符串的主要内容,如果未能解决你的问题,请参考以下文章