「清晰&图解」巧妙的动态规划
Posted 力扣加加
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了「清晰&图解」巧妙的动态规划相关的知识,希望对你有一定的参考价值。
1320. 二指输入的的最小距离
题目描述
二指输入法定制键盘在 XY 平面上的布局如上图所示,其中每个大写英文字母都位于某个坐标处,例如字母 A 位于坐标 (0,0),字母 B 位于坐标 (0,1),字母 P 位于坐标 (2,3) 且字母 Z 位于坐标 (4,1)。
给你一个待输入字符串 word,请你计算并返回在仅使用两根手指的情况下,键入该字符串需要的最小移动总距离。坐标 (x1,y1) 和 (x2,y2) 之间的距离是 |x1 - x2| + |y1 - y2|。
注意,两根手指的起始位置是零代价的,不计入移动总距离。你的两根手指的起始位置也不必从首字母或者前两个字母开始。
示例 1:
输入:word = "CAKE"
输出:3
解释:
使用两根手指输入 "CAKE" 的最佳方案之一是:
手指 1 在字母 'C' 上 -> 移动距离 = 0
手指 1 在字母 'A' 上 -> 移动距离 = 从字母 'C' 到字母 'A' 的距离 = 2
手指 2 在字母 'K' 上 -> 移动距离 = 0
手指 2 在字母 'E' 上 -> 移动距离 = 从字母 'K' 到字母 'E' 的距离 = 1
总距离 = 3
示例 2:
输入:word = "HAPPY"
输出:6
解释:
使用两根手指输入 "HAPPY" 的最佳方案之一是:
手指 1 在字母 'H' 上 -> 移动距离 = 0
手指 1 在字母 'A' 上 -> 移动距离 = 从字母 'H' 到字母 'A' 的距离 = 2
手指 2 在字母 'P' 上 -> 移动距离 = 0
手指 2 在字母 'P' 上 -> 移动距离 = 从字母 'P' 到字母 'P' 的距离 = 0
手指 1 在字母 'Y' 上 -> 移动距离 = 从字母 'A' 到字母 'Y' 的距离 = 4
总距离 = 6
示例 3:
输入:word = "NEW"
输出:3
示例 4:
输入:word = "YEAR"
输出:7
提示:
2 <= word.length <= 300
每个 word[i] 都是一个大写英文字母。
常规做法
思路
我们将左指和右指所在的键位组成,看成一个状态。每次输入一个字母时,则其中一个手指会进行移动,「移动」的过程即是「状态转移」的过程。并且由于字母输入的顺序是固定的,每一个字母都可以看成一个阶段,字母不断输入的过程即是「阶段」的递增,例如第一个字母为第一个阶段,第二个字母为第二个阶段,后面以此类推。
因此,我们需要一个三维的状态来表示整个动态规划的过程,包括当前考虑的「字母下标」,「左指的键位」,「右指的键位」。
二指组成形成的状态:
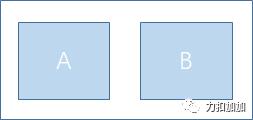
三维状态:

接下来,让我们思考状态如何进行转移。假设字符串为 CAKE,并且此时阶段为 1,即当前考虑字母是 A。在这个阶段下,左右指会存在一种现象,要么左指为 A ,要么右指为 A,此时才能输入字母 A。
对于左指为 A,表示我们通过「移动左指」来到达这个阶段,而右指是「没有移动」的。总结来说,这个阶段下,左指会「变」成 A,右指「不变」。因此,我们需要遍历上一个阶段左指和右指的所有情况,并且转移到下一个阶段时,只移动左指(dp[1][A][R] = Math.min(dp[1][A][R], dp[0][L][R] + move(L, A)))。
注意观察,如果上一个阶段右指为 R,此时这个阶段右指也必须保持不变,同样为 R。
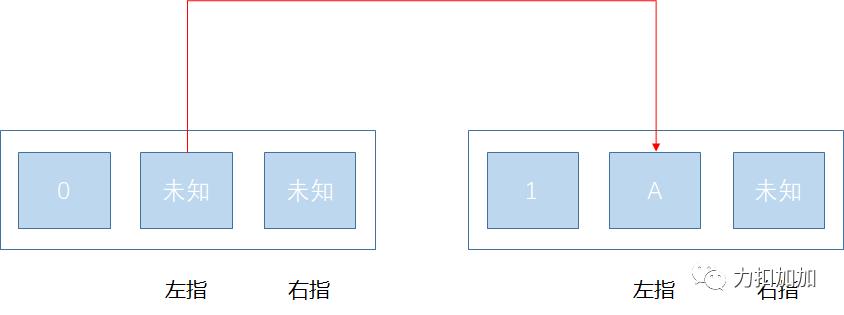
-
阶段 1 的右指和阶段 0 的右指键位相同。 -
阶段 1 的左指键位为 A。
对于右指为 A 的情况同理。
代码
class Solution {
public int minimumDistance(String word) {
// 初始化
int[][][] dp = new int[301][26][26];
for (int i = 1; i <= 300; i++) {
for (int j = 0; j < 26; j++) {
Arrays.fill(dp[i][j], Integer.MAX_VALUE);
}
}
int ans = Integer.MAX_VALUE;
char[] ca = word.toCharArray();
// 遍历每个字母
for (int i = 1; i <= word.length(); i++) {
int v = ca[i - 1] - 'A';
// 遍历上一个阶段左指键位
for (int l = 0; l < 26; l++) {
// 遍历上一个阶段右指键位
for (int r = 0; r < 26; r++) {
// 判断上一个阶段的状态是否存在
if (dp[i - 1][l][r] != Integer.MAX_VALUE) {
// 移动左指
dp[i][v][r] = Math.min(dp[i][v][r], dp[i - 1][l][r] + help(l, v));
// 移动右指
dp[i][l][v] = Math.min(dp[i][l][v], dp[i - 1][l][r] + help(r, v));
}
if (i == word.length()) {
ans = Math.min(ans, dp[i][v][r]);
ans = Math.min(ans, dp[i][l][v]);
}
}
}
}
return ans;
}
// 计算距离
public int help(int a, int b) {
int x = a / 6, y = a % 6;
int x2 = b / 6, y2 = b % 6;
return (int)(Math.abs(x - x2)) + (int)(Math.abs(y - y2));
}
}
「复杂度分析」
-
时间复杂度: ,其中 N 为字符串 word的长度。 -
空间复杂度: ,其中 N 为字符串 word的长度。
空间优化
思路
由于每个阶段只和上个阶段相关,我们可以使用滚动数组思想,循环利用数组,例如 i % 2 代表当前阶段,(i - 1) % 2 代表上一个阶段。
值得注意的是,每次我们计算出新数组后dp[i % 2],需要重新初始化另外一个数组dp[(i - 1) % 2],读者可尝试注释相关代码, 观察结果。
代码
class Solution {
public int minimumDistance(String word) {
// 初始化
int[][][] dp = new int[2][26][26];
for (int i = 0; i < 26; i++) {
Arrays.fill(dp[1][i], Integer.MAX_VALUE);
}
int ans = Integer.MAX_VALUE;
char[] ca = word.toCharArray();
// 遍历每个字母
for (int i = 1; i <= word.length(); i++) {
int v = ca[i - 1] - 'A';
// 遍历上一个阶段左指键位
for (int l = 0; l < 26; l++) {
// 遍历上一个阶段右指键位
for (int r = 0; r < 26; r++) {
// 判断上一个阶段的状态是否存在
if (dp[(i - 1) % 2][l][r] == Integer.MAX_VALUE) {
continue;
}
if (dp[(i - 1) % 2][l][r] != Integer.MAX_VALUE) {
// 移动左指
dp[i % 2][v][r] = Math.min(dp[i % 2][v][r], dp[(i - 1) % 2][l][r] + help(l, v));
// 移动右指
dp[i % 2][l][v] = Math.min(dp[i % 2][l][v], dp[(i - 1) % 2][l][r] + help(r, v));
}
if (i == word.length()) {
ans = Math.min(ans, dp[i % 2][v][r]);
ans = Math.min(ans, dp[i % 2][l][v]);
}
}
}
// 重新初始化另外一个数组
for (int l = 0; l < 26; l++) {
for (int r = 0; r < 26; r++) {
dp[(i - 1) % 2][l][r] = Integer.MAX_VALUE;
}
}
}
return ans;
}
// 计算距离
public int help(int a, int b) {
int x = a / 6, y = a % 6;
int x2 = b / 6, y2 = b % 6;
return (int)(Math.abs(x - x2)) + (int)(Math.abs(y - y2));
}
}
「复杂度分析」
-
时间复杂度: ,其中 N 为字符串 word的长度。 -
空间复杂度:
时间优化
思路
我们再重新观察一下这三个维度信息,分别是:「字母下标」,「左指的键位」,「右指的键位」。由于每次需要按下「一个字母」,左指键位或者右指键位必然有一个是这个「字母的键位」,因此字母下标也「隐含」着一个指头的「键位信息」,使用三个维度显然会有「冗余」,我们可以重新设计一种新的状态:「字母下标」(可以代表「第一个」指头键位),「另外一个指头的键位」。
每次按下一个字母时,要么是字母下标所在的指头(「第一个指头」)移动,要么是「另外一个指头」移动。
第一个指头移动的状态转移图如下:

-
状态 1 的另外一个指头键位等于状态 0 另外一个指头键位 -
dp[1][r] = Math.min(dp[1][r], dp[0][r] + move(word[0], word[1]))
另外一个指头移动的状态转移图如下:
-
注意两个指头顺序交换,第一个指头变成另外一个指头,另外一个指头变成第一个指头。 -
状态 1 的另外一个指头键位等于状态 0 第一个指头键位 -
dp[1][word[0]] = Math.min(dp[1][word[0]], dp[0][r] + move(r, word[1]))
代码
class Solution {
public int minimumDistance(String word) {
// 初始化
int len = word.length();
int ans = Integer.MAX_VALUE;
char[] ca = word.toCharArray();
// 第一个字母的初始值为 0,从第二个字母开始考虑。
int[][] dp = new int[2][26];
Arrays.fill(dp[1], Integer.MAX_VALUE);
// 遍历每个字母
for (int i = 2; i <= word.length(); i++) {
int v = ca[i - 1] - 'A';
// 遍历上一个阶段键位
for (int j = 0; j < 26; j++) {
if (dp[i % 2][j] == Integer.MAX_VALUE) {
continue;
}
int preV = ca[i - 2] - 'A';
dp[(i + 1) % 2][j] = Math.min(dp[(i + 1) % 2][j], dp[i % 2][j] + help(preV, v));
dp[(i + 1) % 2][preV] = Math.min(dp[(i + 1) % 2][preV], dp[i % 2][j] + help(j, v));
if (i == word.length()) {
ans = Math.min(ans, dp[(i + 1) % 2][j]);
ans = Math.min(ans, dp[(i + 1) % 2][preV]);
}
}
Arrays.fill(dp[i % 2], Integer.MAX_VALUE);
}
return ans;
}
// 计算距离
public int help(int a, int b) {
int x = a / 6, y = a % 6;
int x2 = b / 6, y2 = b % 6;
return (int)(Math.abs(x - x2)) + (int)(Math.abs(y - y2));
}
}
「复杂度分析」
-
时间复杂度: ,其中 N 为字符串 word的长度。 -
空间复杂度:
如果该题解对你有帮助,点个赞再走呗~
原文来自:https://leetcode-cn.com/u/hlxing/ 欢迎来撩~
❝点关注,不迷路。如果再给 ➕ 个星标就更棒啦!
❞
推荐阅读
1、
2、
3、
4、
5、
如果觉得文章不错,帮忙点个在看呗
以上是关于「清晰&图解」巧妙的动态规划的主要内容,如果未能解决你的问题,请参考以下文章