文本挖掘 | 高考大纲应该怎么用？
Posted 效率研究所
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了文本挖掘 | 高考大纲应该怎么用？相关的知识，希望对你有一定的参考价值。
高考大纲的文本内涵非常深刻 | 有很多被人忽视的知识点，在《高考大纲》中实际上是被明确要求的，例如：立方差公式。
文章较长，纯干货，建议先转发或收藏，留着慢慢看；
结尾有巨！大！福！利！，别怪我没提醒你。
「以纲为纲」这种口号，在我读高中的时候就有了。
《高考大纲》的确是个好东西，可是大多数情况下高中老师好像很忙的样子，忙着布置各种练习题、模拟题、“预测题”，仿佛这些题目才是根本。而当初说好的「以纲为纲」，就仿佛渣男在床上的甜言蜜语，转过身就忘的一干二净。
实际上，这种舍本逐末的轻佻行为非常危险。
就高考而言，大纲的文字内涵非常深刻。
我举一个简单的例子：
比如在「导数及其应用」这个章节里，有一条不太明显的文本表述——要求同学们可以「根据定义」求解几个常见的幂函数的导数：
| 微信扫码，收听例题讲解音频
而且《高考大纲》对文、理科考生划出了一条不太明显的分界线——是上一页PPT中的绿字儿部分：对理科考生而言，特别要求你们会用定义求解三次函数与根号函数的导数。
幂函数的求导公式相信大家都是懂得的，可能大部分同学会说：能直接用公式，你还用定义，这不是有病吗？
如果你这么认为，那你的学习过程可能就永远损失掉了一个《高考大纲》中明确要求的知识点。
翻开人教版的选修教材，如何使用定义求解根号函数的导数，教材已经写的很详细了：
注意，这个运算过程中本身就蕴含了一个很重要的变形技巧：平方差公式——你注意看第二和第三个等号之间，分子和分母有什么变化就可以了。
三次函数求导的方法教科书里没有写，各位同学也许认为是「类似可得」，但如果你自己真提笔去算，就会发现这还真不是一个依葫芦画瓢就能轻易完成的工作，我给大家做了份笔记：
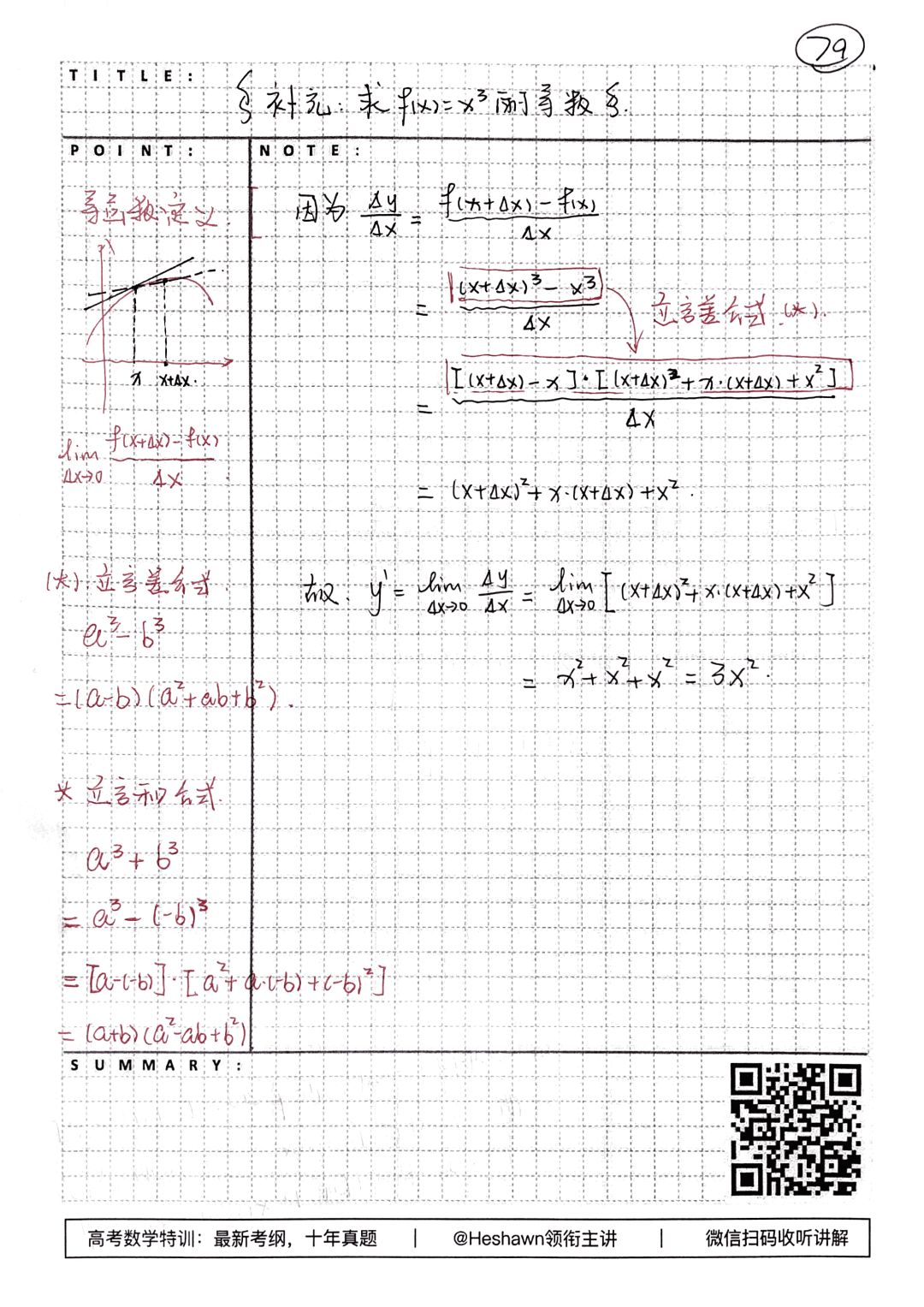| 微信扫码，收听例题讲解音频
——这里面，用到最重要的一项工具，是立方差公式。除非使用这项个等式进行代数变形，否则你是不可能得到最终结果的。
当然，立方差公式衍生的，实际上还有立方和公式——只不过是将（a^3-b^3）当中的b整体代换成(-b)即可。
这个例子就很能说明《高考大纲》的意义何在了。
我不知道今天是不是每一个数学老师都在课堂上为学生强调了「立方差公式」这个东西，也不知道同学们是不是都知道这么个公式——但从《高考大纲》的文本解读而言，立方差公式是一个明确要求所有理科考生必须知道的知识点——因为如果没有这项工具，你是不可能根据定义求解三次函数的导数的。
无论你知不知道这么个东西，但2017年江苏卷最后一道压轴计算题确实用到了这个知识点：
| 微信扫码，收听例题讲解音频
——如果你不懂得用立方和公式对其中各项进行拆分，这道题目基本上就算废了。
考试结束后，有同学拿着参考答案愤愤不平地说：老师，这道题居然需要用立方和公式才能做，明显超纲了啊！
快醒醒吧... 你不能什么题不会做都往「超纲」身上甩锅啊！
# 福利
微信扫码，进入更大世界
﹀
﹀
﹀
以上是关于文本挖掘 | 高考大纲应该怎么用？的主要内容，如果未能解决你的问题，请参考以下文章