广度优先层次遍历还能这么用！

Posted 2021-04-14 PKU软微TQL团队

----树专题三----

树的深度与广度问题

　　昨天我们推送了有关二叉树的构造的问题，如果大家有什么更好的想法或者点子，也欢迎大家与我们交流讨论。今天我们将跟大家分享有关树的深度和广度的问题。

　　所谓树的深度，就是树的最大层次，或者说就是根结点到叶子结点的最短路径的最大长度（也可以称为树的高度），树的广度（宽度）指的是树的某一层的结点数目的最大值。有关树深度的问题，我们可以用深度优先算法解决，或者用递归的思想解决。而关于树的宽度的问题，则可以用广度优先（或者层次遍历）的算法思想解决。我们来看几个例题：

例题1：

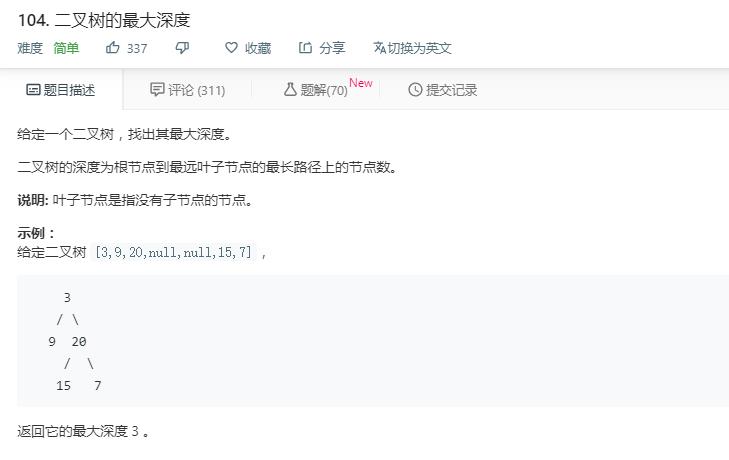
　　先来看一下这道简单的问题，要我们求二叉树的最大深度。无论是关于二叉树的题目还是n叉树的题目，我们都只要灵活地运用树的性质就可以解决。

　　关于树的深度的问题，我们可以利用该性质：对于二叉树来说，其最大深度取决于其左右子树中最大深度较大者；而对于一般树来说，以某一个结点为根结点的树的最大深度取决于其所有子树最大深度的最大值。

　　因此对于二叉树来说，我们只需要递归求出其左右子树的最大深度，那么整个二叉树的最大深度就是左右子树最大深度的较大者加1。(层次遍历也可解哦，自己试试吧！)

C++参考代码：

例题2：

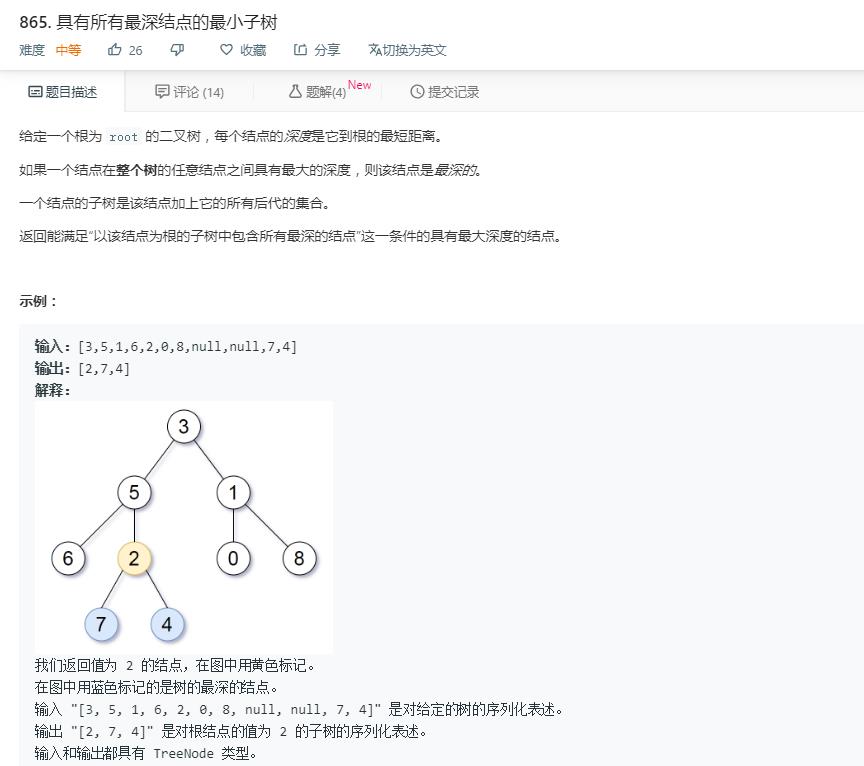
　　我们首先要读懂题目的意思，事实上就是求所有最大深度的叶子结点的公共祖先中最大深度的结点。比如示例中，结点7,4是深度最大的叶子结点，深度均为4，结点2,5,3都是7,4的公共祖先，但是这三个公共祖先结点中，2的深度最大，所以应该返回结点2。

　　一种可行的方法是：我们先通过一次深度优先遍历，确定各个结点的深度，并找到所有深度最大的叶子结点，然后再找到所有最大深度的叶子结点的公共祖先。这种方法交给大家自己去尝试。

　　这里我们介绍另一种方法，思考一下对于某一个结点来说：如果该结点的左子树高度与右子树高度相等，那么说明其左子树和右子树都有深度最大的叶子结点；而如果该结点左子树的高度比右子树的高度高，则说明所有的最大深度的叶子结点只可能在左子树下，而不可能在右子树下；反之亦然。因此，我们可以先求出以各个结点为根结点的树的高度，存入哈希表；然后从根结点开始，根据分析，一步一步确定确定最终结果。

C++参考代码：

例题3：

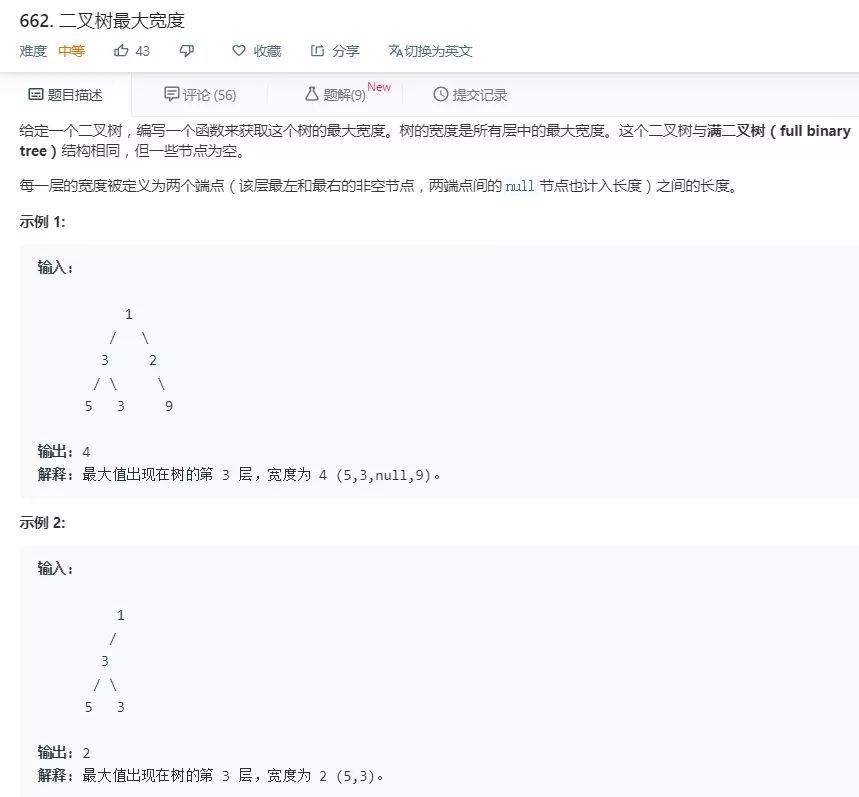
　　相比于简单地求二叉树（或者N叉树）的各层结点数目的最大值，此题中求二叉树的宽度则要复杂一些，因为层间最左和最右的非空结点之间的空节点也算在宽度里面了。我们不能再简单地利用队列模拟层次遍历去求解了，不过我们只需要在层次遍历的基础上，增加一些操作即可。

    我们使用双端队列作为辅助的数据结构，我们依然按照层次遍历的步骤，先将根结点入队，外层循环每一次处理一层；但是不同的是，我们允许队列中有空结点，对于每一层的循环来说，如果队首元素是空结点，那么我们在将队首元素出队之后，再依次入队虚拟的左右子树（均为空结点），如果队首元素是非空结点，那么我们将队首元素出队之后，再依次将其左右子树从队尾入队；此外，还需要在每一层的结点出队完成之后，将队列中（此时队列中元素为下一层的结点）元素从起始位置开始的所有空结点以及从末尾位置开始往前的所有空结点都删去，以保证在处理下一层结点时，队列首尾都是非空结点。

C++参考代码：

　　上面的解法有些浪费资源，这里再给出一个解法，同样是层次遍历，我们记录下结点的序号，将每层的最前和最后结点的序号进行对比，可以得出宽度。

下面的推荐练习题，大家要认真完成哟。

推荐练习题：

Leetcode 111  二叉树的最小深度

Leetcode 559  n叉树的最大深度

Leetcode 543  二叉树的直径