前N项和公式

Posted 2023-03-02

等比，等差前N项和公式是什么啊有几个帮我写几个，最好写一下什么符号都代表什么！谢谢

等差数列前N项和公式：

①Sn=n*a1+n(n-1)d/2

②Sn=n(a1+an)/2

Sn代表项数之和，n代表项数，a1代表数列的第一项，an代表数列的最后一项，d代表数列的公差。

性质：

⑴数列为等差数列的重要条件是：数列的前n项和S 可以写成S = an^2 + bn的形式(其中a、b为常数)．

⑵在等差数列中,当项数为2n (n∈ N+)时,S偶－S奇 = nd,S奇÷S偶=an÷a（n+1） ；当项数为(2n－1）(n∈ N+)时,S奇—S偶=a中 ,S奇÷S偶 =n÷（n-1）．

⑶若数列为等差数列,则S n,S2n －Sn ,S3n －S 2n,…仍然成等差数列,公差为k^2d ．

(4)若数列an与bn均为等差数列,且前n项和分别是Sn和Tn,则am/bm=S2m-1/T2m-1.

⑸在等差数列中,S = a,S = b (n>m),则S = (a－b)．

2. 等比数列前N项和公式：

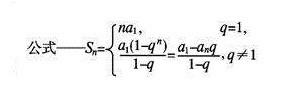
Sn代表项数之和，n代表项数，a1代表数列的第一项，an代表数列的最后一项，q代表数列的公比。

性质：

①若 m、n、p、q∈N，且m+n=p+q，则aman=apaq；

②在等比数列中，依次每 k项之和仍成等比数列；

③若m、n、q∈N，且m+n=2q，则am×an=(aq)^2；

④ 若G是a、b的等比中项，则G2=ab（G ≠ 0）；

⑤在等比数列中，首项a1与公比q都不为零.

⑥在数列an中每隔k(k∈N*)取出一项，按原来顺序排列，所得新数列仍为等比数列且公比为qk+1

⑦当数列an使各项都为正数的等比数列，数列lgan是lgq的等差数列。

参考技术A

通常所说的前n项和的公式包括等差数列和等比数列等。公式如下：

等差数列an的通项公式为：an=a1+(n-1)d。前n项和公式为：Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。注意： 以上n均属于正整数。

等比数列前n项和公式：

若数列｛an｝是公比为q的等比数列，则它的前n项和公式是






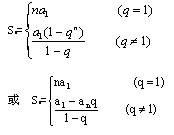
不规则的数列或者规律不明显的数列需要运用多种数学方法，包括归纳法，错位相减法等等。

·关于数列：数列（sequence of number）是以正整数集（或它的有限子集）为定义域的函数，是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项，通常用an表示。

参考技术B (一)1.等差数列an:
通项公式an=a1+(n-1)d 首项a1,公差d, an第n项数
an=ak+(n-k)d ak为第k项数
若a,A,b构成等差数列 则 A=(a+b)/2
2.等差数列前n项和:
设等差数列an的前n项和为Sn
即 Sn=a1+a2+...+an;
那么 Sn=na1+n(n-1)d/2
=dn^2(即n的2次方) /2+(a1-d/2)n
还有以下的求和方法: 1,不完全归纳法 2 累加法 3 倒序相加法
(二)1.等比数列an:
通项公式 an=a1*q^(n-1)(即q的n-1次方) a1为首项,an为第n项
an=a1*q^(n-1,am=a1*q^(m-1))
则an/am=q^(n-m)
(1)an=am*q^(n-m)
(2)a,G,b 若构成等比中项,则G^2=ab (a,b,G不等于0)
(3)若m+n=p+q 则 am*an=ap+aq
2.等比数列前n项和an
设 a1,a2,a3...an构成等比数列
前n项和Sn=a1+a2+a3...an
Sn=a1+a1*q+a1*q^2+....a1*q^(n-2)+a1*q^(n-1)(这个公式虽然是最基本公式,但一部分题目中求前n项和是很难用下面那个公式推倒的,这时可能要直接从基本公式推倒过去,所以希望你这个公式也要理解)
Sn=a1(1-q^n)/(1-q)=(a1-an*q)/(1-q);
注: q不等于1;
Sn=na1 注:q=1
求和一般有以下4个方法: 1,不完全归纳法 2 累乘法 3 错位求和法

参考资料：把我当年课堂笔记翻出来,整理了下...

本回答被提问者采纳 参考技术C 没有公式.不过可以查表得到。
你把每一项都减1就可以看出来。
前n项和相当于是N+（1加1/2。。。一直加到1/N）
括号内部分可以写为Ln(n)+R
其中R是欧拉常数,值约为0.57721566490，或者你写作：1/n[1/(1/n)+1/(2/n)+………+1/（1/n)]=积分
1/xdx（区间是0到1）
这是一个发散级数 参考技术D 等差数列：Sn=a1n+n(n-1)d/2
等比数列：1:q=1时;Sn=na1
2:q#1时;Sn=a1(1-q的n次方）/（1-q）

数列前n项和都有哪些求法？

1、公式法求和
（1）等差数列
(2)等比数列q=i和q≠1
（3）几个常见数列的前n项和：①1+2+3+…+n＝［n（n＋1）］／2
②1＾2＋2＾2＋3＾2+…+n＾2＝［n（n＋1）（2n＋1）］／6
③1＾3＋2＾3＋3＾3＋…+n＾3＝［n（n＋1）］＾2／4
2、倒叙相加法：将一个数列倒过来排列（反序），当它与原来数列对应相加时，如有公因式可提，并且剩余项的和易于求得则可用此法，它是等差数列求和公式的推广。
3、错位相减法（推导等比数列的前n项和公式时所用的方法）
4、裂项相消法：前提是数列中的每一项均能分裂成一正一负两项，一般形如1/a（n+1）an（其中an是等差数列）的数列可用此法。常用裂项技巧有：（1）1/[n(n+k)]=1/k[1/n-1/(n+k)](2)1/(√(n+k)+√n)=1/k[√(n+k)-√n]
(3)1/[(2n+1)(2n-1)]=1/2[1/(2n-1)-1/(2n+1)]
(4)1/[n(n+1)(n+2)]=1/2[1/n(n+1)-1/(n+1)(n+2)]
5、分组转化求和：有一类数列，既不是等差，也不是等比，但若把数列的每一项分成多个项或把数列的项重新组合，就能转化为等差或等比，从而利用等差、等比数列的求和公式解决。 参考技术A 常用的，有两种：（这两个方法，教科书上都有）
一是，等差数列求和方法：倒写相加法
其次，等比数列求和方法：错位相减法
后者用的很多，不仅仅局限于等比数列求和，还适用于一个等差数列乘以一个等比数列构成的新数列的和，即an*bn，其中an是等差数列，公差是d，bn是等比数列，公比是q，
那么an*bn的前n项和
Sn
=
a1*b1
+
a2*b2
+
...
+
an*bn，只要两边同乘以q，
q*Sn
=
a1*b1*q
+
a2*b2*q
+
...
+
an*bn*q
=
a1*b2
+
a2*b3
+
...
+
an*b(n+1)
两式错位相减得
(1-q)*Sn
=
a1*b1
+
d*(b2
+
b3
+
...
+
bn)
-
an*b(n+1)
=
...
后面的应该会了 参考技术B (一）
等差数列的前n项和(分组求和)sn
＝（1＋1）＋[a^(-1)+4]＋[a^(-2)+7]＋……＋[a^(1-n)+(3n-2)]
＝[1＋a^(-1)+a^(-2)＋……＋a^(1-n)]
+
[1＋4＋7+……＋(3n-2)]
前者为等比数列，公比为a^(-1)
后者为等差数列，公差为3
=[1-a^(-n)]/(1-a)+[1+(3n-2)]*n/2
=[1-a^(-n)]/(1-a)+(3n-1)n/2
(裂项法求和
)
这是分解与组合思想在数列求和中的具体应用.
裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的.
通项分解（裂项）如：
（1）1/n(n+1)=1/n-1/(n+1)
（2）1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)]
（3）1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)]
（4）1/(√a+√b)=[1/(a-b)](√a-√b)
（5）
n·n!=(n+1)!-n!
[例]
求数列an=1/n(n+1)
的前n项和.
解：设
an=1/n(n+1)=1/n-1/(n+1)
（裂项）
则
sn=1-1/2+1/2-1/3+1/4…+1/n-1/(n+1)（裂项求和）
＝
1-1/(n+1)
＝
n/(n+1)
小结：此类变形的特点是将原数列每一项拆为两项之后，其中中间的大部分项都互相抵消了。只剩下有限的几项。
注意：
余下的项具有如下的特点
1余下的项前后的位置前后是对称的。
2余下的项前后的正负性是相反的。（二）(1)
等比数列：a
(n+1)/an=q
(n∈n)。
(2)
通项公式：an=a1×q^(n-1)；
推广式：an=am×q^(n-m)；
(3)
求和公式：sn=n×a1
(q=1)
sn=a1(1-q^n)/(1-q)
=(a1-an×q)/(1-q)
(q≠1)
(q为公比，n为项数）