牛顿法，拟牛顿法，共轭梯度法各自的优缺点是啥？

Posted 2023-05-16

各自的算法是怎样的？

参考技术A 牛顿法需要函数的一阶、二阶导数信息，也就是说涉及到Hesse矩阵，包含矩阵求逆运算，虽然收敛速度快但是运算量大。拟牛顿法采用了一定的方法来构造与Hesse矩阵相似的正定矩阵，而这个构造方法计算量比牛顿法要小；共轭梯度法的基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜素，求出目标函数的极小点。根据共轭方向基本性质，这种方法运算量不太大收敛速度也不慢。

牛顿法梯度下降法与拟牛顿法

牛顿法、梯度下降法与拟牛顿法

• 0 引言
• 1 关于泰勒展开式
• • 1.1 原理
  • 1.2 例子
• 2 牛顿法
• • 2.1 x 为一维
  • 2.2 x 为多维
• 3 梯度下降法
• 4 拟牛顿法
• • 4.1 拟牛顿条件
  • 4.2 DFP 算法
  • 4.3 BFGS 算法
  • 4.4 L-BFGS 算法

0 引言

机器学习中在求解非线性优化问题时，常用的是梯度下降法和拟牛顿法，梯度下降法和拟牛顿法都是牛顿法的一种简化

牛顿法是在一个初始极小值点做二阶泰勒展开，然后对二阶泰勒展开式求极值点，通过迭代的方式逼近原函数极值点

在牛顿法迭代公式中，需要求二阶导数，而梯度下降法将二阶导数简化为一个固定正数方便求解

拟牛顿法也是在求解过程中做了一些简化，不用直接求二阶导数矩阵和它的逆

1 关于泰勒展开式

1.1 原理

如果我们有一个复杂函数 $f(x)$, 对这个复杂函数我们想使用 n 次多项式（多项式具有好计算，易求导，且好积分等一系列的优良性质）去拟合这个函数，这时就可以对 $f(x)$进行泰勒展开，求某一点 $x_0$附近的 n 次多项式：

注意：
n 次多项式只是在 $x_0$ 较小的邻域内能较好拟合 $f(x)$，也就是说，泰勒展开式其实是一种局部近似的方法，只近似 $x=x_0$那一点的函数性

1.2 例子

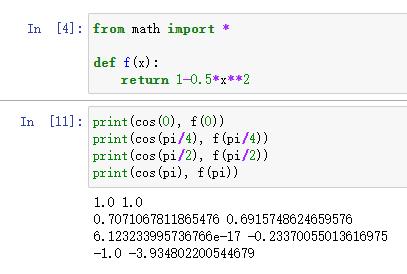
现在要求 $f(x)=cos(x)$ 在 $x_0=0$ 处的二阶泰勒展开，因为我们去掉了高阶项，所以只是近似

直接套用公式
$f(x_0)=f(0)=cos(0)=1$
$f^{\prime }(x_0)=f^{\prime }(0)=-sin(0)=0$
$f^{\prime \prime }(x_0)=f^{\prime \prime }(0)=-cos(0)=-1$
所以展开后的公式为
$$f(x)\approx f(x_0)+f^{\prime }(x_0)\ast x+f^{\prime \prime }(x_0)\ast x^2/2=1-0.5\ast x^2$$

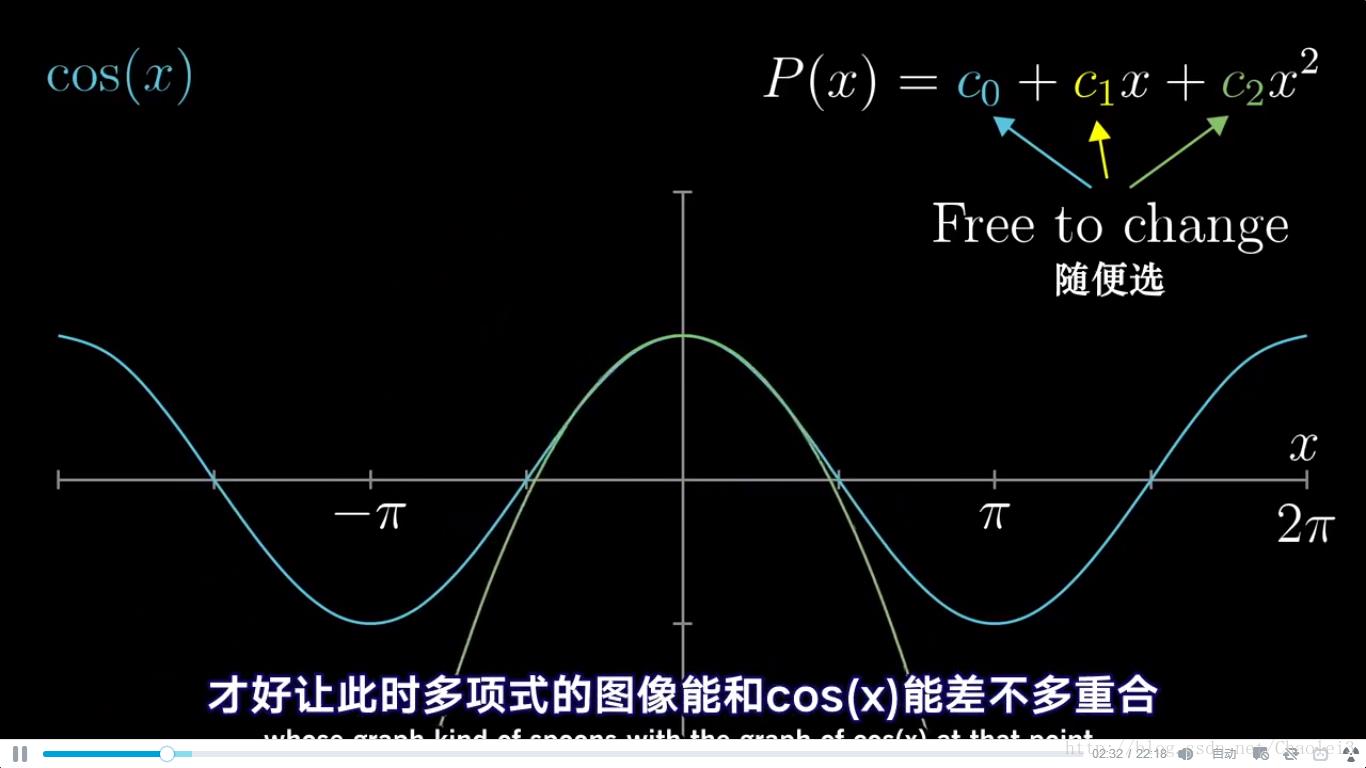
从下方运行程序可以看出，离展开点越近的点，拟合程度越高，越远的点，越离谱

2 牛顿法

2.1 x 为一维

现在假设我们有目标函数 $f(x)$，我们希望求此函数的极小值，牛顿法的基本思想是：随机找到一个点设为当前极值点 $x_k$，在这个点对 $f(x)$ 做二次泰勒展开，进而找到极小点的下一个估计值。在 $x_k$ 附近的二阶泰勒展开为：

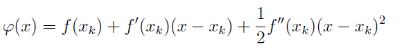
现在想求 $\phi (x)$ 的极值点，由极值的必要条件可知，$\phi (x)$ 应满足导数为 0，即：
$${\phi }^{\prime }(x)=0$$
即
$${\phi }^{\prime }(x)=f^{\prime }(x_k)+f^{\prime \prime }(x_k)(x-x_k)=0$$
这样就可以求得 x 的值
$$x=x_k-\frac{f^{\prime }(x_k)}{f^{\prime \prime }(x_k)}$$
于是给定初始值 $x_0$,就可以通过迭代的方式逼近$f(x)$的极值点：
$$x_{k+1}=x_k-\frac{f^{\prime }(x_k)}{f^{\prime \prime }(x_k)}$$

如下图，首先在 $x_n$ 处泰勒展开，得到$f(x)$ 的近似函数 $g_n(x)$ ，求得 $g_n(x)$ 的极值点 $x_{n+1}$

随后在 $x_{n+1}$ 出泰勒展开，得到$g_{n+1}(x)$ 函数，继续求$g_{n+1}(x)$ 的极值点

一直迭代最后就会逼近 $f(x)$ 的极值点

2.2 x 为多维

上面讨论的是参数 x 为一维的情况，当 x 有多维时，二阶泰勒展开式可以做推广，此时：
$$\phi (x)\&\#$$