数据结构 实验6 堆和搜索树
Posted 山大软院苏苏
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构 实验6 堆和搜索树相关的知识,希望对你有一定的参考价值。
实验六 堆和搜索树
一、 要求完成时间
实验开始后的第七周之前完成
二、 实验目的
掌握堆和搜索树的基本概念,插入、删除方法。
三、 实验内容
1、 输入一系列不为零的正整数(最多不超过20个),遇到0代表输入结束(不包含0)。
2、 根据上面输入的数据序列,用初始化方法创建最大堆(不要用节点依次插入的办法创建最大堆),然后输出最大堆的层次序列。
3、 输出用堆排序后的排序结果。
4、 根据上面输入的数据,创建二叉搜索树(关键字不允许重复,如遇重复,则不重复插入该关键字),输出二叉搜索树的前序序列、中序序列(分行输出)。
四、 测试用例及答案
测试如下所有用例及答案,且确保运行后出现完全一样的输出,
(操作系统提示“请按任意键继续….”等,可以不一样。)
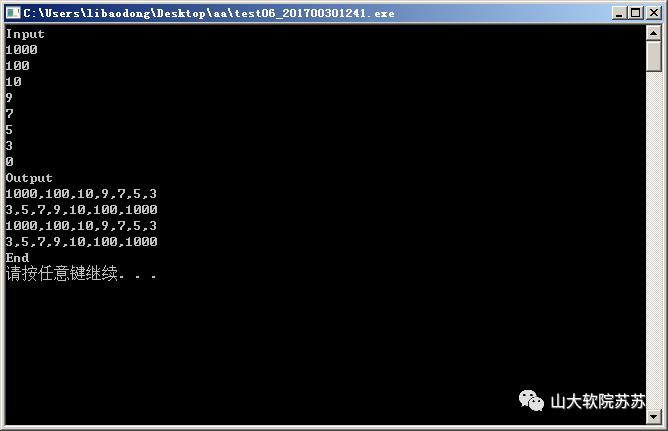
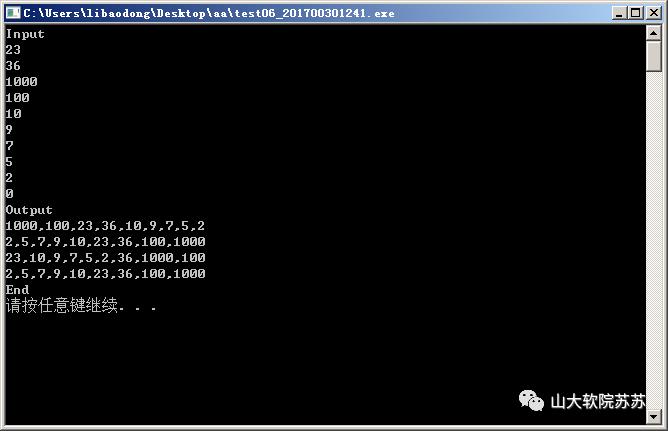
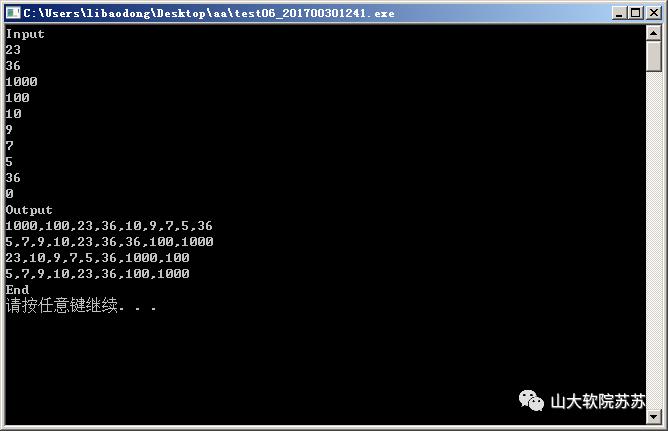
分析:
1.堆排序:借助最大堆的定义,返回的肯定是堆内最大的元素,将堆内的元素依次弹出,直到堆为空。这样就实现了排序。
2.BSTree继承自前面实验的BinaryTree以减少类方法的设计。只需根据二叉搜索树的定义,在插入、删除时,根据元素的大小遍历左子树或右子树。
以下是代码,有点略多,仅供参考,希望你写出更好的方法!
代码:
#include<iostream>
#include<string>
using namespace std;
class OutOfBounds {
public:
OutOfBounds(){
cout<<"Out of bounds!"<<endl;
}
};
class NoMen{
public:
NoMen(){
cout<<"NoMen error!"<<endl;
}
};
//处理数BadInput的报错
class BadInput{
public:
BadInput(){
cout<<"BadInput!"<<endl;
}
};
class NoElement{
public:
NoElement(){
cout<<"NoElement!"<<endl;
}
};
//类最大堆
template<class T>
class MaxHeap{
public:
MaxHeap(int MaxHeapSize = 10);
~MaxHeap(){delete [] heap;}
int Size() const{return CurrentSize;}
T Max(){if(CurrentSize == 0) throw OutOfBounds();
return heap[1];}
MaxHeap<T>& Insert(const T& x);
MaxHeap<T>& DeleteMax(T& x);
void Initialize(T a[],int size,int ArraySize);
void Output();
private:
int CurrentSize,MaxSize;
T *heap;//元素数组
};
template<class T>
MaxHeap<T>::MaxHeap(int MaxHeapSize){
MaxSize = MaxHeapSize;
heap = new T[MaxSize+1];
CurrentSize = 0;
}
template<class T>
MaxHeap<T>& MaxHeap<T>::Insert(const T& x){
//把x插入到最大堆中
if(CurrentSize == MaxSize)
throw NoMen();
//为x寻找插入位置
//i从新的叶节点开始,并沿着树上升
int i = ++CurrentSize;
while(i != 1 && x > heap[i/2]){
//不能够把x放入heap[i]
heap[i] = heap[i/2];//将元素下移
i /= 2;//移向父节点
}
heap[i] = x;
return *this;
}
template<class T>
MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x){
//将最大元素放入x,并从堆中删除最大元素
//检查堆是否为空
if(CurrentSize == 0)
throw OutOfBounds();
x = heap[1];
//重构堆
T y = heap[CurrentSize--];
//从根节点开始,为y寻找合适的位置
int i = 1;//堆的当前节点
int ci = 2;//i的孩子
while(ci <= CurrentSize){
//heap[ci]应是i的比较大的孩子
if(ci < CurrentSize && heap[ci] < heap[ci+1])
ci++;
if(y >= heap[ci])
break;
heap[i] = heap[ci];
i = ci;
ci *= 2;
}
heap[i] = y;
return *this;
}
template<class T>
void MaxHeap<T>::Initialize(T a[],int size,int ArraySize){
//把最大堆初始化为数组a
delete [] heap;
heap = a;
CurrentSize = size;
MaxSize = ArraySize;
//产生一个最大堆
for(int i = CurrentSize/2;i >= 1;i--){
T y = heap[i];//子树的根
//寻找放置y的位置
int c = 2*i;//c的父节点是y的目标位置
while(c <= CurrentSize){
if(c < CurrentSize && heap[c] < heap[c+1])
c++;
if(y >= heap[c])
break;
heap[c/2] = heap[c];
c *= 2;
}
heap[c/2] = y;
}
}
template<class T>
void MaxHeap<T>::Output(){
for(int i = 1;i <= MaxSize;i++){
cout<<heap[i];
if(i != MaxSize)
cout<<",";
}
}
//类BinaryTreeNode
template<class T>
class BinaryTreeNode {
public:
BinaryTreeNode() {LeftChild=RightChild=NULL;}
BinaryTreeNode(const T&e)
{
data=e;
LeftChild=RightChild=NULL;
}
BinaryTreeNode(const T&e, BinaryTreeNode *l,
BinaryTreeNode *r)
{
data=e;
LeftChild=l;
RightChild=r;
}
BinaryTreeNode<T> *LeftChild; //左子树
BinaryTreeNode<T> *RightChild; //右子树
T data;
};
//类BinaryTree
template<class T>
class BinaryTree{
public:
BinaryTree(){root=NULL;}
~BinaryTree(){Delete();}
void Delete(){PostOrder(Free, root); root=0;}
static void Free(BinaryTreeNode<T>* t){delete t;}
int IsEmpty()const
{return ((root) ? 0 : 1);}
int Root(T& x)const;
void MakeTree(const T& element, BinaryTree<T>& left,
BinaryTree<T>& right);
void BreakTree(T& element, BinaryTree<T>& left,
BinaryTree<T>& right);
void PreOrder(void(*Visit)(BinaryTreeNode<T> *u))
{PreOrder(Visit, root);}
void InOrder(void(*Visit)(BinaryTreeNode<T> *u))
{InOrder(Visit, root);}
void PostOrder(void(*Visit)(BinaryTreeNode<T> *u))
{PostOrder(Visit, root);}
BinaryTreeNode<T>* root; //根节点指针
//遍历方法
void PreOrder(void(*Visit)
(BinaryTreeNode<T> *u), BinaryTreeNode<T> *t);
void InOrder(void(*Visit)
(BinaryTreeNode<T> *u), BinaryTreeNode<T> *t);
void PostOrder(void(*Visit)
(BinaryTreeNode<T> *u), BinaryTreeNode<T> *t);
//为了输出,
void PreOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i);
void InOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i);
void PostOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i);
static void Output(BinaryTreeNode<T> *t)
{
cout << t->data << " ";
}
static void Output2(BinaryTreeNode<T> *t,int i)
{
if(i != 0)cout<<",";
cout<<t->data;
}
void PreOutput()
{
static int i = 0;PreOrder(Output2,root,i);
cout << endl;
}
void InOutput()
{
static int i = 0;InOrder(Output2,root,i);
cout << endl;
}
void PostOutput()
{
static int i = 0;PostOrder(Output2,root,i);
cout << endl;
}
};
//类BSTree
template<class E, class K>
class BSTree : public BinaryTree<E>{
public:
int Search(const K& k, E& e)const;
BSTree<E,K>& Insert(const E& e);
BSTree<E,K>& Delete(const K& k, E& e);
//在e中存储树的最大元素
void MaxNode(E& e)const;
};
/*---------------------BinaryTree Methods()-------------------------*/
template<class T>
int BinaryTree<T>::Root(T& x) const
{ //取根节点的data域,放入x
//如果没有根节点,则返回false
if(root)
{
x=root->data;
return 1;
}
else return 0; //没有根节点
}
template<class T>
void BinaryTree<T>::MakeTree(const T& element,
BinaryTree<T>& left, BinaryTree<T>& right)
{//将left, right,和 element 合并成一棵新树
//left, right和 this必须是不同的树
//创建新树
root=new BinaryTreeNode<T>(element, left.root, right.root);
//阻止访问left和right
left.root=right.root=0;
}
template<class T>
void BinaryTree<T>::BreakTree(T& element,
BinaryTree<T>& left, BinaryTree<T>& right)
{//left, right和 this必须是不同的树
//检查树是否为空
if(!root) //空树
throw BadInput();
//分解树
element=root->data;
left.root=root->LeftChild;
right.root=root->RightChild;
delete root;
root=0;
}
template<class T>
void BinaryTree<T>::PreOrder(void(*Visit)
(BinaryTreeNode<T>* u), BinaryTreeNode<T>* t)
{//前序遍历
if(t)
{
Visit(t);
PreOrder(Visit, t->LeftChild);
PreOrder(Visit, t->RightChild);
}
}
template<class T>
void BinaryTree<T>::InOrder(void(*Visit)(BinaryTreeNode<T>* u),
BinaryTreeNode<T>* t)
{//中序遍历
if(t)
{
InOrder(Visit, t->LeftChild);
Visit(t);
InOrder(Visit, t->RightChild);
}
}
template<class T>
void BinaryTree<T>::PostOrder(void(*Visit)(BinaryTreeNode<T>* u),
BinaryTreeNode<T>* t)
{//后序遍历
if(t)
{
PostOrder(Visit, t->LeftChild);
PostOrder(Visit, t->RightChild);
Visit(t);
}
}
//为了输出,
template<class T>
void BinaryTree<T>::PreOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i){
if(t){
Visit(t,i);
PreOrder(Visit,t->LeftChild,++i);
PreOrder(Visit,t->RightChild,++i);
}
}
template<class T>
void BinaryTree<T>::InOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i){
if(t){
InOrder(Visit,t->LeftChild,i);
if(t->LeftChild)i++;
Visit(t,i++);
InOrder(Visit,t->RightChild,i);
}
}
template<class T>
void BinaryTree<T>::PostOrder(void(*Visit)(BinaryTreeNode<T> *u,int i),BinaryTreeNode<T> *t,int i){
if(t){
PostOrder(Visit,t->LeftChild,i);
PostOrder(Visit,t->RightChild,i);
Visit(t,i++);
}
}
/*----------------------End of BinaryTree Methods()------------------*/
/*------------------------BSTree Methods()---------------------------*/
template<class E, class K>
int BSTree<E,K>::Search(const K& k, E& e) const
{//搜索与k匹配的元素
//指针p从树根开始进行查找
BinaryTreeNode<E> *p=this->root;
while(p) //检查p->data
{
if(k<p->data)
p=p->LeftChild;
else if(k>p->data)
p=p->RightChild;
else{ //找到元素
e=p->data;
return 1;
}
}
return 0;
}
template<class E, class K>
BSTree<E,K>& BSTree<E,K>::Insert(const E& e)
{ //如果不出现重复,则插入e
BinaryTreeNode<E> *p=NULL; //搜索指针
BinaryTreeNode<E> *pp=NULL; //p的父节点指针
//寻找插入点
p=this->root; //p is now the root
while(p)
{
pp=p;
//将p移向孩子节点
if(e<p->data)
p=p->LeftChild;
else if(e>p->data)
p=p->RightChild;
else
return *this; //出现重复,不插入,直接返回
}
//为e建立一个节点,并将该节点连接至to pp
BinaryTreeNode<E> *r=new BinaryTreeNode<E>(e);
if(this->root)
{//树非空
if(e<pp->data)
pp->LeftChild=r;
else if(e>pp->data)
pp->RightChild=r;
}
else //插入到空树中
this->root=r;
return *this;
}
template<class E, class K>
BSTree<E,K>& BSTree<E,K>:: Delete(const K& k, E& e)
{//删除关键值为k的元素,并将其放入e
//将p指向关键值为k的节点
BinaryTreeNode<E> *p=NULL; //搜索指针
BinaryTreeNode<E> *pp=NULL; //p的父节点指针
p=this->root;
while(p && p->data != k)
{//移动到p的孩子
pp=p;
if(k < p->data)
p=p->LeftChild;
else
p=p->RightChild;
}
if(!p) //没有关键值为k的元素
throw NoElement();
e=p->data; //保存欲删除的元素
//对树进重构
if(p->LeftChild && p->RightChild) //处理p有两个孩子的情形
{//转换成有0或1个孩子的情形
//在p的左子树中寻找最大元素
BinaryTreeNode<E> *s=p->LeftChild;
BinaryTreeNode<E> *ps=p; //s的父节点
while(s->RightChild)
{//移动到较大的元素
ps=s;
s=s->RightChild;
}
//将最大元素从s移动到p
p->data=s->data;
p=s;
pp=ps;
}//end all if
//p最多有一个孩子
//在c中保存孩子节点
BinaryTreeNode<E> *c;
if(p->LeftChild)
c=p->LeftChild;
else
c=p->RightChild;
//删除p
if(p==this->root)
this->root=c;
else{
//p是pp的左孩子还是pp的右孩子?
if(p==pp->LeftChild)
pp->LeftChild=c;
else
pp->RightChild=c;
}
delete p;
return *this;
}
template<class E, class K>
void BSTree<E,K>::MaxNode(E &e)const
{//function returns max. value of tree (rightmost value)
BinaryTreeNode<E>* p=NULL; //root node
BinaryTreeNode<E>* pp=NULL; //parent of p
p=this->root;
while(p)
{
pp=p;
p=p->RightChild;
}
//p points to NULL, pp points to node before NULL
e=pp->data; //max. value stored
}
int main(){
//最大堆部分
BSTree<int,int> abst;
int a [22];
int length = 0;
cout<<"Input"<<endl;
for(int i = 0;i < 21;i++){
cin>>a[i+1];
if(a[i+1] != 0)
abst.Insert(a[i+1]);
if(a[i+1] == 0)break;
length++;
}
cout<<"Output"<<endl;
//初始化最大堆
MaxHeap<int> oneMaxHeap;
oneMaxHeap.Insert(0);
oneMaxHeap.Initialize(a,length,length);
oneMaxHeap.Output();
cout<<endl;
//堆排序
int array[length];
for(int i = 0;i < length;i++){
oneMaxHeap.DeleteMax(array[length-1-i]);
}
for(int i = 0;i < length;i++){
cout<<array[i];
if(i != length-1)
cout<<",";
}
cout<<endl;
//二叉搜索树部分
abst.PreOutput();
abst.InOutput();
cout<<"End"<<endl;
return 0;
}
运行截图:
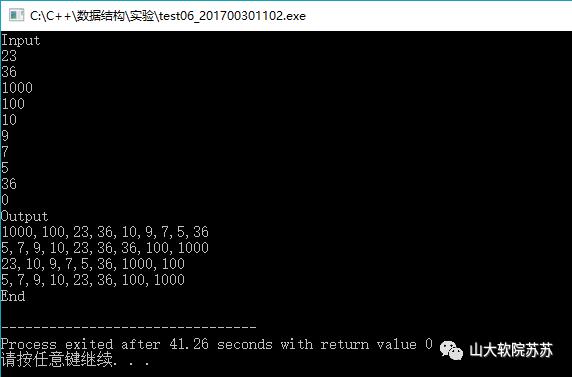
ps:
多敲代码,丰衣足食。
END
以上是关于数据结构 实验6 堆和搜索树的主要内容,如果未能解决你的问题,请参考以下文章