数据结构(荣誉)实验三 搜索树
Posted 上山打老虎D
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构(荣誉)实验三 搜索树相关的知识,希望对你有一定的参考价值。
1. 过河问题–搜索树
题目描述
多个囚犯参与者要过河,其中只有监管者一人可以划船。小船每次最多载两人过河。监管者不在时,已有积怨的囚犯可能会斗殴。请问他们该如何安全过河?
假设一开始所有人都在河的左岸,用0表示,如果成功过河,则到达河的右岸,用1表示。
请采用BFS求解,并输出过河过程。
输入
首先输入要过河的人数n(包括监管者和囚犯)
接着输入监管者的编号s(假设每个人的编号从0开始,编号最小的在最右边)
然后输入有积怨的囚犯的对数m
接下来m行,两两输入有积怨的囚犯编号
输出
如有解,输出划船过河方案,即每一步的状态,也就是每个人此时在河的左岸还是右岸。初始状态全部为0。
否则,输出No solution
样例输入
4
3
2
0 1
1 2
样例输出
0000
1010
0010
1011
0001
1101
0101
1111
题解
#include<iostream>
#include<stack>
#include <vector>
#include <map>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
vector<PII> limits;
class Node {
public:
string data;
Node() {
data = "";
}
Node(string str) {
this->data = str;
}
};
int admin;
int n;
bool isOK(Node node) {
for (auto i = limits.begin(); i != limits.end(); i++) {
if (node.data[i->first] != node.data[admin] && node.data[i->first] == node.data[i->second]) {
return false;
}
}
return true;
}
bool isFinish(Node node) {
for (int i = 0; i < n; i++) {
if (node.data[i] != '1') {
return false;
}
}
return true;
}
int main() {
int num;
cin >> n >> admin >> num;
admin = n - admin - 1;
while (num--) {
int temp1, temp2;
cin >> temp1 >> temp2;
limits.emplace_back(n - temp1 - 1, n - temp2 - 1);
}
queue<Node> dataQueue;
map<string, string> dataMap;
Node start;
for (int i = 0; i < n; i++) {
start.data += '0';
}
dataMap[start.data] = "finish";
dataQueue.push(start);
while (!dataQueue.empty()) {
for (int i = n - 1; i >= 0; i--) {
Node temp(dataQueue.front());
if (temp.data[i] == temp.data[admin] && i != admin) {
if (temp.data[i] == '0') {
temp.data[i] = '1';
} else {
temp.data[i] = '0';
}
}
if (temp.data[admin] == '0') {
temp.data[admin] = '1';
} else {
temp.data[admin] = '0';
}
if (!isOK(temp) || dataMap.count(temp.data)) {
continue;
}
dataMap[temp.data] = dataQueue.front().data;
dataQueue.push(temp);
if (isFinish(temp)) {
string str = temp.data;
vector<string> resData;
while (str != "finish") {
resData.push_back(str);
str = dataMap[str];
}
for(int i=resData.size()-1;i>=0;i--){
cout<<resData[i]<<endl;
}
return 0;
}
}
dataQueue.pop();
}
cout << "No solution" << endl;
return 0;
}
2. 八数码问题–搜索树
题目描述
在3×3的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。
给出一种初始状态S0和目标状态Sg,请找到一种最少步骤的移动方法,实现从初始状态S0到目标状态Sg的转变。
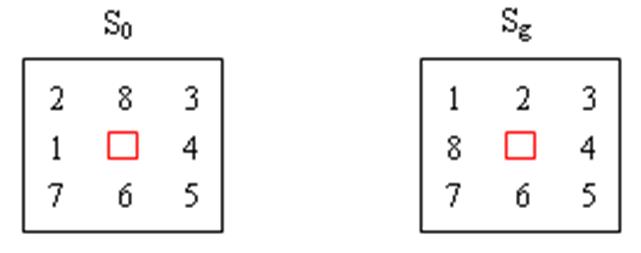
输入
输入测试次数t
对于每次测试,首先输入一个初始状态S0,一行九个数字,空格用0表示。然后输入一个目标状态Sg,一行九个数字,空格用0表示。
输出
只有一行,该行只有一个数字,表示从初始状态S0到目标状态Sg需要的最少移动次数(测试数据中无特殊无法到达目标状态数据)
样例输入
2
283104765
123804765
283104765
283164705
样例输出
4
1
题解
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <string>
#include <vector>
using namespace std;
class Node
{
public:
string data;
int depth;
Node() {}
Node(string data, int depth)
{
this->data = data;
this->depth = depth;
}
};
bool isFind(queue<Node> q, string str)
{
while (!q.empty())
{
if (q.back().data == str)
{
return true;
}
q.pop();
}
return false;
}
int main()
{
int t;
cin >> t;
while (t--)
{
string startData;
string endData;
cin >> startData >> endData;
queue<Node> statusQueue;
Node root(startData, 0);
statusQueue.push(root);
bool flag = false;
if (startData == endData)
{
cout << "0" << endl;
continue;
}
while (true)
{
if (flag)
{
break;
}
Node temp(statusQueue.front().data, statusQueue.front().depth);
statusQueue.pop();
int position = temp.data.find_first_of('0');
// cout << temp.data << endl;
// cout << position << endl;
for (int i = 0; i < 4; i++)
{
int x = position / 3;
int y = position % 3;
if (i == 0)
{
x++;
}
else if (i == 1)
{
x--;
}
else if (i == 2)
{
y++;
}
else
{
y--;
}
if (x < 0 || y < 0 || x > 2 || y > 2 || 3 * x + y > 8 || 3 * x + y < 0)
{
continue;
}
Node nextNode(temp.data, temp.depth + 1);
nextNode.data[position] = nextNode.data[3 * x + y];
nextNode.data[3 * x + y] = '0';
if (nextNode.data == endData)
{
flag = true;
cout << nextNode.depth << endl;
break;
}
if (isFind(statusQueue, nextNode.data))
{
//cout << "FIND" << endl;
}
else
{
statusQueue.push(nextNode);
}
}
}
}
return 0;
}
3.骑士
题目描述
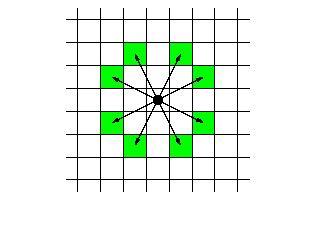
国际象棋中骑士的走法如图所示。
请计算给定骑士在棋盘上的起点,走到终点所需最少步数。
输入
每个测试包括一行,为用空格隔开的起点和终点。每个点由字母表示的列+数字表示的行组成。
输出
最少步数
样例输入
e2 e4
a1 b2
b2 c3
a1 h8
样例输出
2
4
2
6
题解
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <string>
using namespace std;
class Point {
public:
int x, y;
Point() {};
Point(int x, int y) {
this->x = x;
this->y = y;
}
};
class Node {
public:
Point point;
int depth;
Node() {};
Node(Point p, int depth) {
point.x = p.x;
point.y = p.y;
this->depth = depth;
}
Node(int x, int y, int depth) {
point.x = x;
point.y = y;
this->depth = depth;
}
};
bool isMeet(Point a, Point b) {
if (a.x == b.x && a.y == b.y) {
return true;
}
return false;
}
int main() {
char a, b;
int c, d;
while (cin >> a >> c >> b >> d) {
bool flag = false;
Point startPoint(a - 'a' + 1, c);
Point endPoint(b - 'a' + 1, d);
if (isMeet(startPoint, endPoint)) {
cout << "0" << endl;
break;
}
Node startNode(startPoint, 0);
queue<Node> pointQueue;
pointQueue.push(startNode);
while (true) {
Node temp(pointQueue.front());
pointQueue.pop();
for (int i = 0; i < 8; i++) {
Point newPoint;
if (i == 0) {
newPoint.x = temp.point.x - 2;
newPoint.y = temp.point.y + 1;
} else if (i == 1) {
newPoint.x = temp.point.x - 1;
newPoint.y = temp.point.y + 2;
} else if (i == 2) {
newPoint.x = temp.point.x + 1;
newPoint.y = temp.point.y + 2;
} else if (i == 3) {
newPoint.x = temp.point.x + 2;
newPoint.y = temp.point.y + 1;
} else if (i == 4) {
newPoint.x = temp.point.x + 2;
newPoint.y = temp.point.y - 1;
} else if (i == 5) {
newPoint.x = temp.point.x + 1;
newPoint.y = temp.point.y - 2;
} else if (i == 6) {
newPoint.x = temp.point.x - 2;
newPoint.y = temp.point.y - 1;
} else {
newPoint.x = temp.point.x - 1;
newPoint.y = temp.point.y - 2;
}
if (newPoint.x > 0 && newPoint.x < 9 && newPoint.y > 0 && newPoint.y < 9) {
if (isMeet(newPoint, endPoint)) {
flag = true;
cout << temp.depth + 1 << endl;
break;
} else {
Node newNode(newPoint, temp.depth + 1);
pointQueue.push(newNode);
}
} else {
continue;
}
}
if (flag) {
break;
}
}
}
return 0;
}
以上是关于数据结构(荣誉)实验三 搜索树的主要内容,如果未能解决你的问题,请参考以下文章