分析时间与空间复杂度《三钻数据结构与算法笔记》
Posted 技术银河
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分析时间与空间复杂度《三钻数据结构与算法笔记》相关的知识,希望对你有一定的参考价值。
本文是覃超老师的《算法训练营》的学习笔记,此笔记的内容包含了学习后的个人记录、个人总结、理解和思想。从而更好的学习算法。
前言
学习任何一门知识的时候,我们需要分析清楚这门知识的核心是什么,从而在这个核心中我们可以得到什么。如果我们是盲目的吸收知识,其实很多知识我们都是在目前场景、工作、生活中无法使用的。也是因为学习之后无法运用,所以我们很快就会遗忘,或者是在学习的过程中很容易就会放弃。
在一生的学习的过程中,发现学习我们急需使用或者能给我们及时带来价值的知识,我们会学的更加牢固,更加能坚持学习。
学习《数据结构与算法》这门知识的核心是什么?又能得到什么呢?
-
弄懂编程的底层逻辑; -
在编程的过程中,拥有一个哆啦A梦一样百宝工具袋; -
在遇到性能问题的时候,有算法的思维逻辑和规则来解决问题; -
提高编程思维;
这篇笔记记录了算法的核心时间和空间复杂度,《数据结构与算法》都是围绕着这个核心开展的。它的存在也是为了解决我们在编程的过程中性能问题,同时也让我们有更高级的思维和思路,写出更优质的程序。

复杂度指标 Big O Notation
-
O (1): 常数复杂度 - Constant Complexity -
O (log n): 对数复杂度 - Logarithmic Complexity -
O (n): 线性复杂度 - Linear Complexity -
O (n^2): 平方复杂度 - N square Complexity -
O (2^n): 指数 - Exponential Growth -
O (n!): 阶乘 - Factorial
如何看时间复杂度
-
分析函数; -
根据n的不同情况会运行多少次; -
最后得出一个平均的运行次数的量级;
Complexity 例子
O (1) - 常数复杂度
let n = 1000;
console.log("Hello - your input is: " + n)
O (N) - 线性复杂度
for (let i = 1; i <= n; i++) {
console.log("Hello world - your input is: " + i)
}
O (N^2)
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
console.log("Hello world - your input is: " + i + " and " + j)
}
}
那如果我们不是嵌套两层
for循环,是把两个循环分开来存放呢?这种方式时间复杂度是?
for (let i = 1; i <= n; i++) {
console.log("Hello world - your i input is: " + i)
}
for (let j = 1; j <= n; j++) {
console.log("Hello world - your j input is: " + j)
}
很多小伙伴应该猜到了,就是2* n次的复杂度,那就是O(2n)。其实还是O(n)的时间复杂度。
O(log(n))
for (let i = 1; i < n; i = i * 2) {
console.log("Hello world - your input is: " + i);
}
O(k^n)
// Fibonacci递归
function fib (n) {
if (n <= 2) return n;
return fib(n-1) + fib(n-2);
}
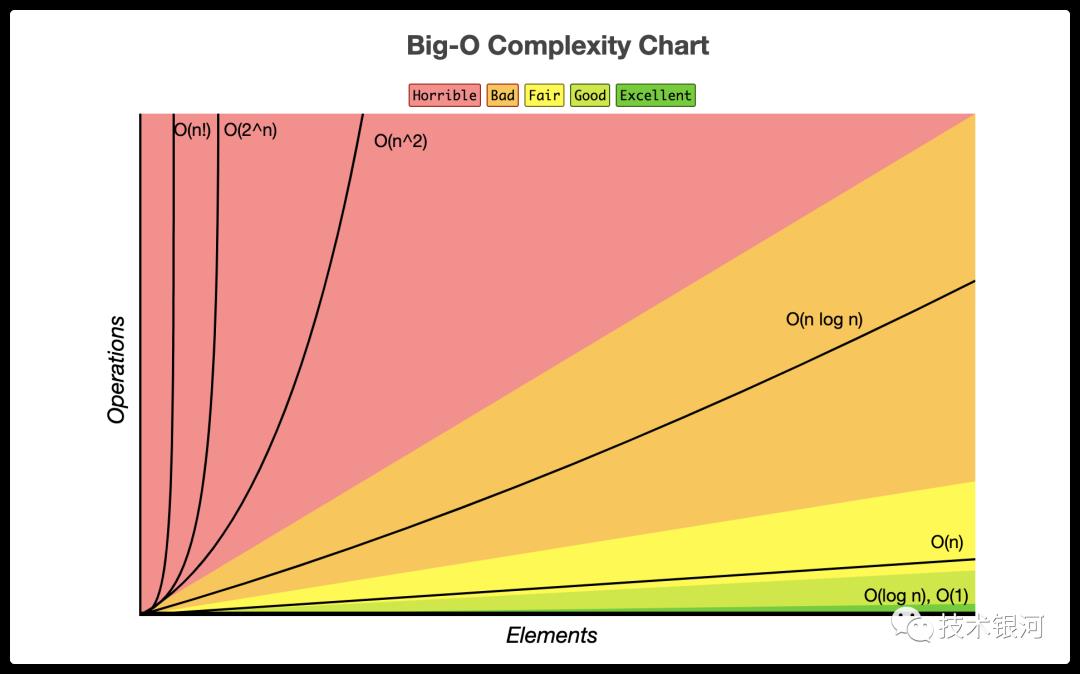
时间复杂度曲线
-
y轴是Operations就是操作复杂度的指数; -
x轴是Elements就是n我们的循环次数 ; -
这里我们可以看到在 n比较小的时候,复杂度是相对稳定的; -
但是当 n越来越大时,Big-O复杂度就会急速飙升;
所以在我们写程序的时候,如果能把时间和空间复杂度从
O(n^2)降到O(n)或者O(1)后,我们得到的优化收益是非常高的!
-
在编写程序的时候一定要注意到它的时间和空间复杂度,这样编写的时候就能预测出这段代码的性能级别; -
用最简洁的时间和空间复杂度完成这段程序; -
这样就是最顶尖的职业编程选手了; -
因为复杂度越高,程序损耗的时间(处理时间)和资源(内存)就越大;
降低时间和空间复杂度
我们用个例子就可以看到如何在编程中降低复杂度:
计算:1 + 2 + 3 + ... + n
方法一:循环1到n然后累加 (时间复杂度 O(n))
let sum = 0
for (let i = 1; i < n; i++) {
sum += i
}
console.log(sum)
方法二:求和公式 sum = n(n+1)/2 (时间复杂度 O(1))
let sum = n * (n + 1) / 2
console.log(sum)
注意:
在做题或者面试的时候先 确认题目,确保一切的条件和题目的理解无误;想出所有可能的解决方案;同时 比较每个方法的时间和空间复杂度;接下来 找出最优的解决方案(时间最快,内存使用最少)
判断时间和空间复杂度
斐波那契(Fibonacci)例子
公式:F(n) = F(n - 1) + F(n - 2)
我们可以直接使用递归来解题:
function fib(n) {
if (n <= 2) return n
return fib(n - 1) + fib(n - 2)
}
-
这个 fib斐波那契函数中是一个递归; -
每一次传入一个 n值时,都会循环递归fib方法来一层一层往下计算; -
最后到达 n小于2,返回最后的n值;
那针对这个递归,我们怎么计算它的时间复杂度呢?
-
要推断出这个程序的 复杂度,首先我们要知道具体在这个函数中程序做了什么; -
我们距离现在传入 n为6,那就是运行fib(6) -
这个时候 6被传入这个方法,然后返回的就是fib(5)+fib(4),这时fib(5)和fib(4)就会再进入fib函数,这里就分开了两个分支了。以此类推我们就会出现以下一个树状过程:
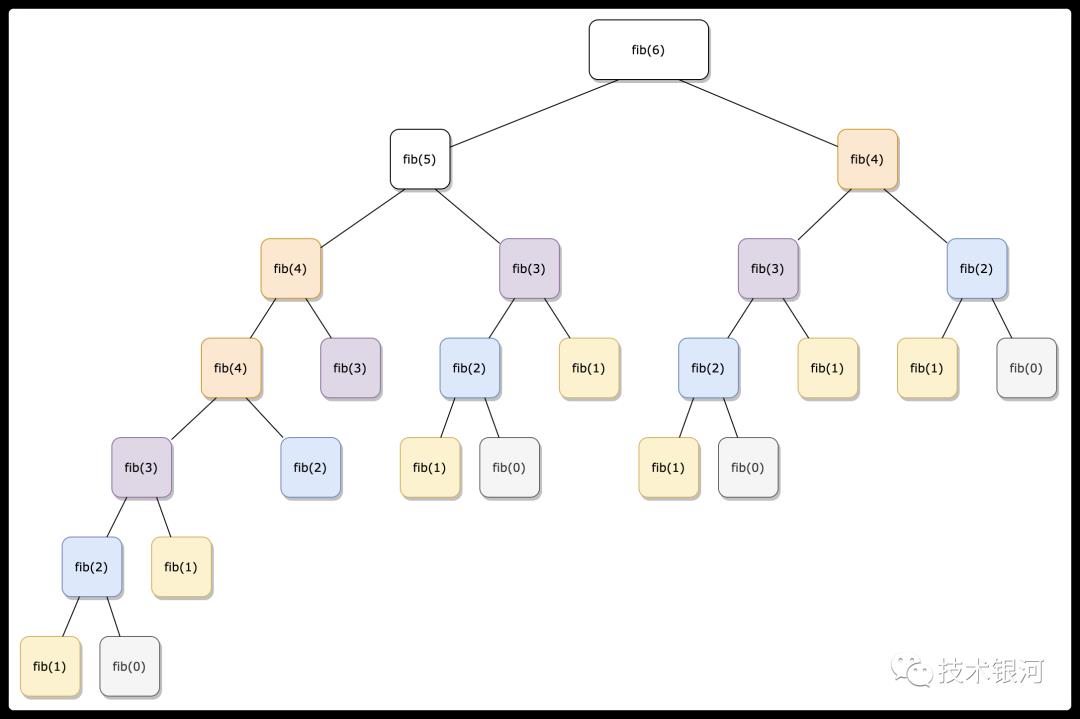
-
通过上图展开来的树,我们可以看到每一层是上一层的2倍: fib(6)展开为fib(5)+fib(4),然后fib(5)和fib(4)又展开了两个。 -
所以 fibonacci的执行次数就是一个指数级 - O(2^n) -
这里我们也可以看到 fib(3)、fib(4)等等,都被重复计算了多次,所以这个计算的 复杂度高达2的6次方; -
所以在做题和面试的时候就 不要运用上面的代码实例,我们要加入缓存机制, 缓存重复计算的结果或者用 一个循环来写,从而降低这个程序的复杂度。
主定理 Master Theorem
任何一个分治或者递归函数都可以通过这个定理来算出它们的时间复杂度。这个定理里面有4种最常用的,只要记住这4种就可以了。
| 算法 (Algorithem) | 时间复杂度 (Run time) |
|---|---|
| 二分查找 (Binary search) | O(log n) |
| 二叉树遍历 (Binary tree traversal) | O(n) |
| 排序二维矩阵 (Optimal sorted matrix search) | O(n) |
| 归并排序 (Merge sort) | O(n log n) |
常见面试题
-
二叉树遍历中的前序、中序、后序:时间复杂度是多少? -
时间复杂度是 O(n),无论是前序、中序或者后序每一个节点都会访问一次,并且仅访问一次; -
所以就是二叉树的节点总数,也就是 O(n)的线性时间复杂度; -
图的遍历:时间复杂度是多少? -
时间复杂也是 O(n), 这里的n就是图里面的节点总数; -
搜索算法:DFS、BFS时间复杂度是多少? -
DFS是深度优先,BFS是广度优先算法。 -
不管是深度优先还是广度优先,因为访问的节点只访问一次,所以时间复杂度也是 O(n)的。(n指的是搜索空间里面的节点总数) -
二分查找:时间复杂度是多少? -
答案是 O(log n)
总结
-
程序复杂度:Big O Notation -
O (1), O(log n), O(n), O(n^2), ... 等等,越复杂程序性能越差; -
分析复杂度法则:分析代码的逻辑,找到程序中运行的次数; -
降低程序时间和空间复杂度可以提升代码的质量,同时优化程序的性能; -
主定理: -
所有的 分治或者 递归函数都可以通过 主定理来分析出它的 时间复杂度; -
常见面试题: -
二叉树遍历中的前序、中序、后序:时间复杂度是多少? - O(n) -
图的遍历:时间复杂度是多少? - O(n) -
搜索算法:DFS、BFS时间复杂度是多少? - O(n) -
二分查找:时间复杂度是多少? - O(log n)
我是三钻,一个在技术银河中等你们一起来终身漂泊学习。点赞是力量,关注是认可,评论是关爱!下期再见
以上是关于分析时间与空间复杂度《三钻数据结构与算法笔记》的主要内容,如果未能解决你的问题,请参考以下文章