树的深度优先搜索(上)

Posted 2021-04-11 Alleria Windrunner

还记得我们说迭代法的具体应用中的二分法吗？我们讨论了一个查字典的例子。如果要使用二分查找，我们首先要把整个字典排个序，然后每次都通过二分的方法来缩小搜索范围。

不过在平时的生活中，咱们查字典并不是这么做的。我们都是从单词的最左边的字母开始，逐个去查找。比如查找“boy”这个单词，我们一般是这么查的。首先，在 a～z 这 26 个英文字母里找到单词的第一个字母 b，然后在 b 开头的单词里找到字母 o，最终在 bo 开头的单词里找到字母 y。

你可以看我画的这种树状图，其实就是从树顶层的根结点一直遍历到最下层的叶子结点，最终逐步构成单词字典的过程。对应的数据结构就是字典树（prefix tree），或者叫字典树（trie）。

那字典树究竟该如何构建呢？有了字典树，我们又该如何查询呢？本篇，我们从图论的基本概念出发，来给你讲一下什么样的结构是树，以及如何通过树的深度优先搜索，来实现字典树树的构建和查询。

图论的一些基本概念

字典树是一种有向树。那什么是有向树？顾名思义，有向树就是一种树，特殊的就是，它的边是有方向的。而树是没有简单回路的连通图。

如果一个图里所有的边都是有向边，那么这个图就是有向图。如果一个图里所有的边都是无向边，那么这个图就是无向图。既含有向边，又含无向边的图，称为混合图。

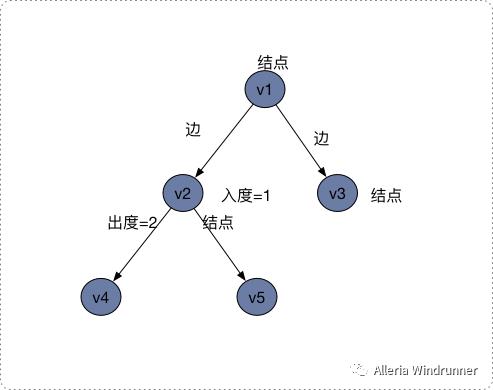
在有向图中，以结点 v 为出发点的边的数量，我们叫作 v 的出度。而以 v为 终点的边之数量，称为 v 的入度。在上图中，结点 v2 的入度是 1，出度是 2。

还有两个和有向树有关的概念，回路和连通，我这里简单给你解释一下，你很容易就能明白了。

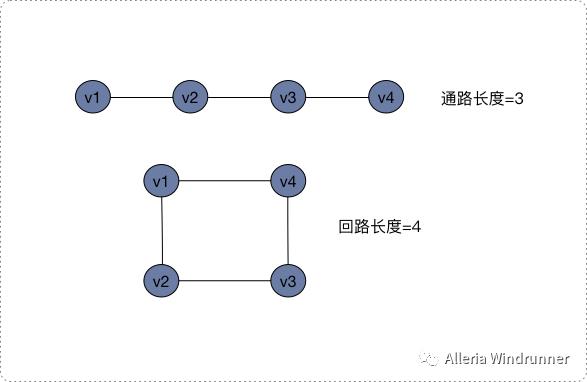
结点和边的交替序列组成的就是通路。所以，通路上的任意两个结点其实就是互为连通的。如果一条通路的起始点 v1 和终止点 vn 相同，这种特殊的通路我们就叫作回路。从起始点到终止点所经过的边之数量，就是通路的长度。示意图如下，这里面有 1 条通路和 1 条回路，第一条非回路通路的长度是 3，第二条回路的长度是 4。

理解了图的基本概念，我们再来看树和有向树。树是一种特殊的图，它是没有简单回路的连通无向图。这里的简单回路，其实就是指，除了第一个结点和最后一个结点相同外，其余结点不重复出现的回路。

那么，什么是有向树呢？顾名思义，有向树是一种特殊的树，其中的边都是有向的，而且它满足以下几个条件：

• 有且仅有一个结点的入度为 0，这个结点被称为根；
• 除根以外的所有结点，入度都为 1。从树根到任一结点有且仅有一条有向通路。

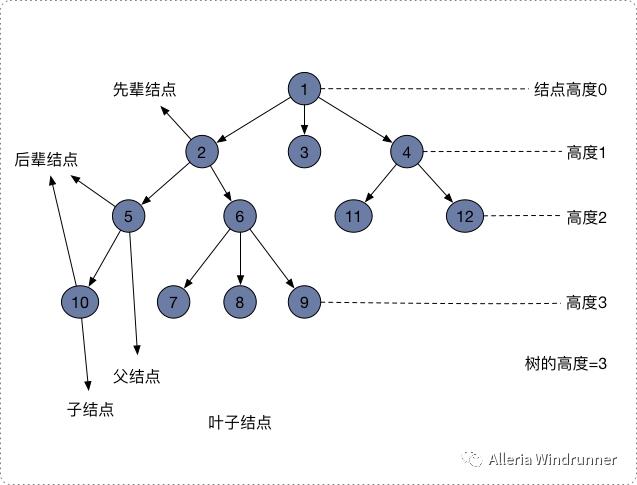
除了这些基本定义，有向树还有几个重要的概念，父结点、子结点、兄弟结点、先辈结点、后辈结点、叶子结点、结点的高度（或深度）、树的高度（或深度）。

字典树的构建和查询

好了，说了这么些，你对有向树应该有了理解。接下来，我们来看，如何使用有向树来实现字典树呢？这整个过程主要包括两个部分：构建字典树和查询字典树。

构建字典树

首先，我们把空字符串作为树的根。对于每个单词，其中每一个字符都代表了有向树的一个结点。而前一个字符就是后一个字符的父结点，后一个字符是前一个字符的子结点。这也意味着，每增加一个字符，其实就是在当前字符结点下面增加一个子结点，相应地，树的高度也增加了 1。

我们以单词 eleven 为例，从根结点开始，第一次我增加字符 e，在根结点下增加一个“e”的结点。第二次，我在“e”结点下方增加一个“l”结点。以此类推，最终我们可以得到下面的树。

查询字典树

假设我们已经使用牛津词典，构建完了一个完整的字典树，现在我们就能按照开篇所说的那种方式，查找任何一个单词了。从字典树的根开始，查找下一个结点，顺着这个通路走下去，一直走到到某个结点。如果这个结点及其字典代表了一个存在的单词，而待查找的单词和这个结点及其字典正好完全匹配，那就说明成功找到了一个单词。否则，就表示无法找到。

这里还有几种特殊情况，需要注意。

• 如果还没到叶子结点的时候，待查的单词就结束了。这个时候要看最后匹配上的非叶子结点是否代表一个单词；如果不是，那说明被查单词并不在字典中。
• 如果搜索到字典树的叶子结点，但是被查单词仍有未处理的字母。由于叶子结点没有子结点，这时候，被查单词不可能在字典中。
  如果搜索到一半，还没到达叶子结点，被查单词也有尚未处理的字母，但是当前被处理的字母已经无法和结点上的字符匹配了。这时候，被查单词不可能在字典中。
  
  

字典树的构建和查询这两者在本质上其实字典是一致的。构建的时候，我们需要根据当前的字典进行查询，然后才能找到合适的位置插入新的结点。而且，这两者都存在一个不断重复迭代的查找过程，我们把这种方式称为深度优先搜索（Depth First Search）。

所谓树的深度优先搜索，其实就是从树中的某个结点出发，沿着和这个结点相连的边向前走，找到下一个结点，然后以这种方式不断地发现新的结点和边，一直搜索下去，直到访问了所有和出发点连通的点、或者满足某个条件后停止。

如果到了某个点，发现和这个点直接相连的所有点都已经被访问过，那么就回退到在这个点的父结点，继续查看是否有新的点可以访问；如果没有就继续回退，一直到出发点。由于单棵树中所有的结点都是连通的，所以通过深度优先的策略可以遍历树中所有的结点，因此也被称为深度优先遍历。

其中，结点上的数字表示结点的 ID，而虚线表示遍历前进的方向，结点边上的数字表示该结点在深度优先搜索中被访问的顺序。在深度优先的策略下，我们从点 110 出发，然后发现和 110 相连的点 123，访问 123 后继续发现和 12字典3 相连的点 162，再往后发现 162 没有出度，因此回退到 123，查看和 123 相连的另一个点 587，根据 587 的出度继续往前推进，如此类推。

把深度优先搜索，和在字典树中查询单词的过程对比一下，你就会发现两者的逻辑是一致的。不过，使用字典树匹配某个单词的时候，只需要沿着一条可能的通路搜索下去，而无需遍历树中所有的结点。