树的广度优先搜索(上)

Posted 2021-04-13 Alleria Windrunner

上一篇我们探讨了如何在树的结构里进行深度优先搜索。说到这里，有一个问题，不知道你有没有思考过，树既然是两维的，我们为什么一定要朝着纵向去进行深度优先搜索呢？是不是也可以朝着横向来进行搜索呢？本篇我们就来看另一种搜索机制，广度优先搜索。

社交网络中的好友问题

LinkedIn、Facebook、微信、QQ 这些社交网络平台都有大量的用户。在这些社交网络中，非常重要的一部分就是人与人之间的“好友”关系。

在数学里，为了表示这种好友关系，我们通常使用图中的结点来表示一个人，而用图中的边来表示人和人之间的相识关系，那么社交网络就可以用图论来表示。而“相识关系”又可以分为单向和双向。

单向表示，两个人 a 和 b，a 认识 b，但是 b 不认识 a。如果是单向关系，我们就需要使用有向边来区分是 a 认识 b，还是 b 认识 a。如果是双向关系，双方相互认识，因此直接用无向边就够了。

从上面的例图可以看出，人与人之间的相识关系，可以有多条路径。比如，张三可以直接连接赵六，也可以通过王五来连接赵六。比较这两条通路，最短的通路长度是 1，因此张三和赵六是一度好友。也就是说，这里我用两人之间最短通路的长度，来定义他们是几度好友。照此定义，在之前的社交关系示意图中，张三、王五和赵六互为一度好友，而李四和赵六、王五为二度好友。

寻找两个人之间的最短通路，或者说找出两人是几度好友，在社交中有不少应用。例如，向你推荐新的好友、找出两人之间的关系的紧密程度、职场背景调查等等。在 LinkedIn 上，有个功能就是向你推荐了你可能感兴趣的人。下面这张图是我的 LinkedIn 主页里所显示的好友推荐。

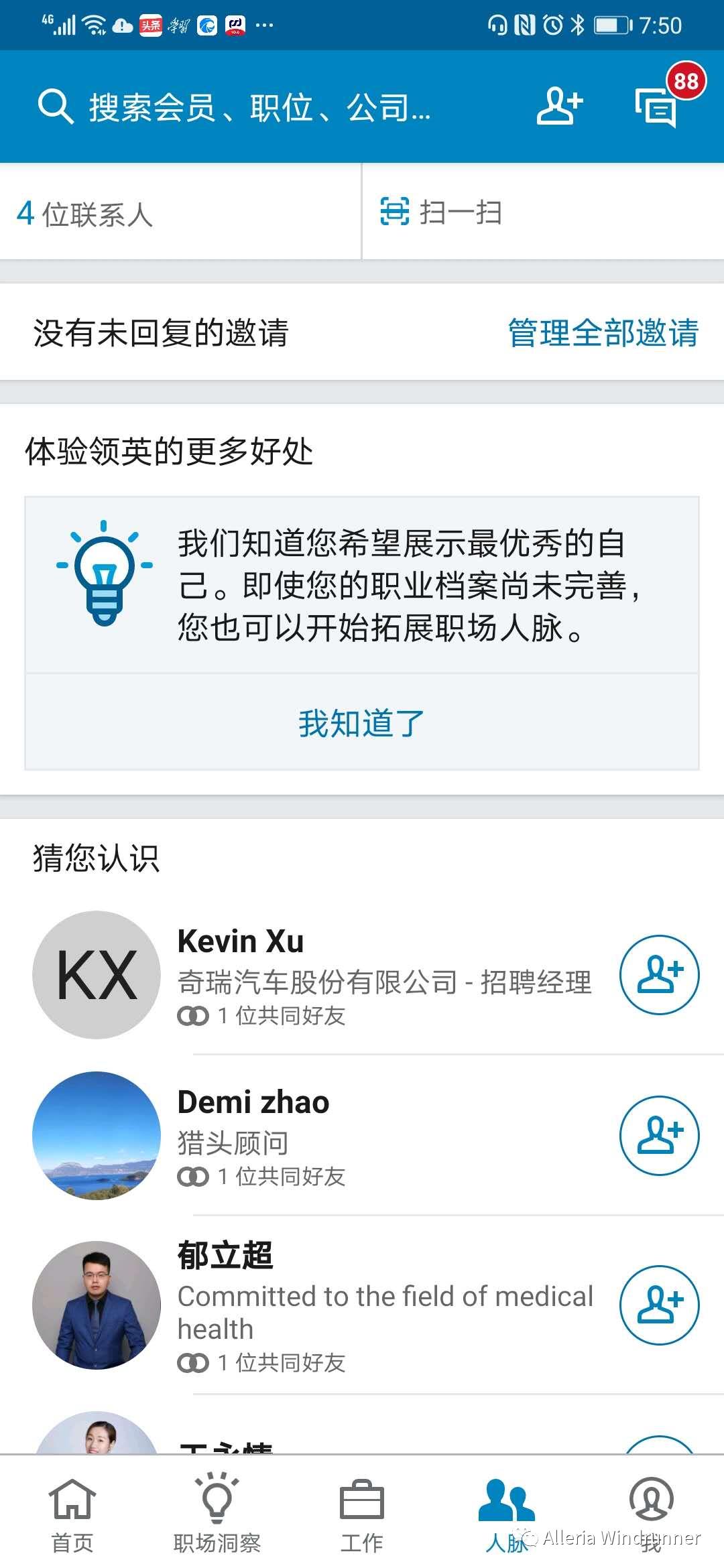
这些被推荐的候选人，和我都有不少的共同连接，也就是共同好友。所以他们都是我的二度好友。但是，他们和我之间还没有建立直接的联系，因此不是一度好友。也就是说，对于某个当前用户，LinkedIn 是这么来选择好友推荐的：

• 被推荐的人和当前用户不是一度好友；
• 被推荐的人和当前用户是二度好友。

那为什么我们不考虑“三度“甚至是“四度”好友呢？我前面已经说过，两人之间最短的通路长度，表示他们是几度好友。那么三度或者四度，就意味着两人间最短的通路也要经历 2 个或更多的中间人，他们的关系就比较疏远，互相添加好友的可能性就大大降低。

所以呢，总结一下，如果我们想进行好友推荐，那么就要优先考虑用户的“二度“好友，然后才是“三度”或者“四度”好友。那么，下一个紧接着要面临的问题就是：给定一个用户，如何优先找到他的二度好友呢？

深度优先搜索面临的问题

这种情况下，你可能会想到上一篇介绍的深度优先搜索。深度优先搜索不仅可以用在树里，还可以应用在图里。不过，我们要面临的问题是图中可能存在回路，这会增加通路的长度，这是我们在计算几度好友时所不希望的。所以在使用深度优选搜索的时候，一旦遇到产生回路的边，我们需要将它过滤。具体的操作是，判断新访问的点是不是已经在当前通路中出现过，如果出现过就不再访问。

如果过滤掉产生回路的边，从一个用户出发，我们确实可以使用深度优先的策略，搜索完他所有的 n 度好友，然后再根据关系的度数，从二度、三度再到四度进行排序。这是个解决方法，但是效率太低了。为什么呢？

你也许听说过社交关系的六度理论。这个理论神奇的地方在于，它说地球上任何两个人之间的社交关系不会超过六度。咋一听，感觉不太可能。仔细想想，假设每个人平均认识 100 个人（我真心不觉得 100 很多，不信你掰着指头数数看自己认识多少人），那么你的二度好友就是 100^2，这个可以用我们前面讲的排列思想计算而来。

以此类推，三度好友是 100^3，到五度好友就有 100 亿人了，已经超过了地球目前的总人口。即使存在一些好友重复的情况下，例如，你的一度好友可能也出现在你的三度好友中，那这也不可能改变结果的数量级。所以目前来看，地球上任何两个人之间的社会关系不会超过六度。

六度理论告诉我们，你的社会关系会随着关系的度数增加，而呈指数级的膨胀。这意味着，在深度搜索的时候，每增加一度关系，就会新增大量的好友。但是你仔细回想一下，当我们在用户推荐中查看可能的好友时，基本上不会看完所有推荐列表，最多也就看个几十个人，一般可能也就看看前几个人。所以，如果我们使用深度优先搜索，把所有可能的好友都找到再排序，那效率实在太低了。

广度优先搜索

更高效的做法是，我们只需要先找到所有二度的好友，如果二度好友不够了，再去找三度或者四度的好友。这种好友搜索的模式，其实就是我们今天要介绍的广度优先搜索。

广度优先搜索（Breadth First Search），也叫宽度优先搜索，是指从图中的某个结点出发，沿着和这个点相连的边向前走，去寻找和这个点距离为 1 的所有其他点。只有当和起始点距离为 1 的所有点都被搜索完毕，才开始搜索和起始点距离为 2 的点。当所有和起始点距离为 2 的点都被搜索完了，才开始搜索和起始点距离为 3 的点，如此类推。

我用上一篇介绍深度优先搜索顺序的那棵树，带你看一下广度优先搜索和深度优先搜索，在结点访问的顺序上有什么不一样。

同样，我们用结点上的数字表示结点的 ID，用虚线表示遍历前进的方向，用结点边上的数字表示该结点在广度优先搜索中被访问的顺序。从这个图中，你有没有发现，广度优先搜索其实就是横向搜索一颗树啊！

尽管广度优先和深度优先搜索的顺序是不一样的，它们也有两个共同点。

第一，在前进的过程中，我们不希望走重复的结点和边，所以会对已经被访问过的点做记号，而在之后的前进过程中，就只访问那些还没有被标记的点。这一点上，广度优先和深度优先是一致的。有所不同的是，在广度优先中，如果发现和某个结点直接相连的点都已经被访问过，那么下一步就会看和这个点的兄弟结点直接相连的那些点，从中看看是不是有新的点可以访问。

例如，在上图中，访问完结点 945 的两个子结点 580 和 762 之后，广度优先策略发现 945 没有其他的子结点了，因此就去查看 945 的兄弟结点 131，看看它有哪些子结点可以访问，因此下一个被访问的点是 906。而在深度优先中，如果到了某个点，发现和这个点直接相连的所有点都已经被访问过了，那么不会查看它的兄弟结点，而是回退到这个点的父节点，继续查看和父结点直接相连的点中是不是存在新的点。例如在上图中，访问完结点 945 的两个子结点之后，深度优先策略会回退到点 110，然后访问 110 的子结点 131。

第二，广度优先搜索也可以让我们访问所有和起始点相通的点，因此也被称为广度优先遍历。如果一个图包含多个互不连通的子图，那么从起始点开始的广度优先搜索只能涵盖其中一个子图。这时，我们就需要换一个还没有被访问过的起始点，继续广度优先遍历另一个子图。

如何实现社交好友推荐？

之前我说深度优先是利用递归的嵌套调用、或者是栈的数据结构来实现的。然而，广度优先的访问顺序是不一样的，我们需要优先考虑和某个给定结点距离为 1 的所有其他结点。等距离为 1 的结点访问完，才会考虑距离为 2 的结点。等距离为 2 的结点访问完，才会考虑距离为 3 的结点等等。在这种情况下，我们无法不断地根据结点的边走下去，而是要先遍历所有距离为 1 的点。

那么，如何在记录所有已被发现的结点情况下，优先访问距离更短的点呢？仔细观察，你会发现和起始点更近的结点，会先更早地被发现。也就是说，越早被访问到的结点，越早地处理它，这是不是很像我们平时排队的情形？早到的人可以优先接受服务，而晚到的人需要等前面的人都离开，才能轮到。所以这里我们需要用到队列这种先进先出（First In First Out）的数据结构。

如果你不是很熟悉队列的数据结构，我这里简短地回顾一下。队列是一种线性表，要被访问的下一个元素来自队列的头部，而所有新来的元素都会加入队列的尾部。

我画了张图给你讲队列的工作过程。首先，读取已有元素的时候，都是从队列的头部来取，例如 x1，x2 等等。所有新的元素都加入队列的尾部，例如 xm，xm+1。

那么在广度优先搜索中，队列是如何工作的呢？这主要分为以下几个步骤。

首先，把初始结点放入队列中。然后，每次从队列首位取出一个结点，搜索所有在它下一级的结点。接下来，把新发现的结点加入队列的末尾。重复上述的步骤，直到没有发现新的结点为止。

• 第 1 步，将初始结点 110 加入队列中。
• 第 2 步，取出结点 110，搜出下一级结点 123、879、945 和 131。
• 第 3 步，将点 123、879、945 和 131 加入队列的末尾。
• 第 4 步，重复第 2 和第 3 步，处理结点 123，将新发现结点 162 和 587 加入队列末尾。
• 第 5 步，重复第 2 和第 3 步，处理结点 879，没有发现新结点。
• 第 6 步，重复第 2 和第 3 步，处理结点 945，将新发现的结点 580 和 762 加入队列末尾。
• 第 n-1 步，重复第 2 和第 3 步，处理结点 906，没有发现新结点。
• 第 n 步，重复第 2 和第 3 步，处理结点 681，没有发现新的结点，也没有更多待处理的结点，整个过程结束。

理解了如何使用队列来实现广度优先搜索之后，我们就可以开始着手编写代码。我们现在没有现成的用户关系网络数据，所以我们需要先模拟生成一些用户结点及其间的相识关系，然后利用队列的数据结构进行广度优先的搜索。基于此，主要使用的数据结构包括：

• 用户结点 Node。这次设计的用户结点和前缀树结点 TreeNode 略有不同，包含了用户的 ID user_id，以及这个用户的好友集合。我用 HashSet 实现，便于在生成用户关系图的时候，确认是否会有重复的好友。
• 表示整个图的结点数组 Node[]。由于每个用户使用 user_id 来表示，所以我可以使用连续的数组表示所有的用户。用户的 user_id 就是数组的下标。
• 队列 Queue。由于 Java 中 Queue 是一个接口，因此需要用一个拥有具体实现的 LinkedList 类。

public class Node {  public int user_id; // 结点的名称，这里使用用户id public HashSet<Integer> friends = null;  // 使用哈希映射存放相连的朋友结点。哈希便于确认和某个用户是否相连。 public int degree; // 用于存放和给定的用户结点，是几度好友  // 初始化结点 public Node(int id) { user_id = id; friends = new HashSet<>(); degree = 0; } }

我们可以用代码随机生成用户间的关系。首先根据指定的用户数量，生成 Node[]数组，以及数组中的每个用户的节点 Node。然后根据边的数量，生成用户之间的相识关系。需要注意的是，自己不能是自己的好友，而且某个用户的所有好友之中不能有重复的人。

Node[] user_nodes = new Node[user_num];
// 生成所有表示用户的结点for (int i = 0; i < user_num; i++) { user_nodes[i] = new Node(i);}
// 生成所有表示好友关系的边for (int i = 0; i < relation_num; i++) { int friend_a_id = rand.nextInt(user_num); int friend_b_id = rand.nextInt(user_num); if (friend_a_id == friend_b_id) continue;  // 自己不能是自己的好友。如果生成的两个好友id相同，跳过 Node friend_a = user_nodes[friend_a_id]; Node friend_b = user_nodes[friend_b_id];
 friend_a.friends.add(friend_b_id); friend_b.friends.add(friend_a_id);}

其中，user_num- 用户的数量，也就是结点的数量。relation_num- 好友关系的数量，也就是边的数量。由于 HashSet 有去重的功能，所以我这里做了简化处理，没有判断是否存在重复的边，也没有因为重复的边而重新生成另一条边。

随后我们的主角，广度优先搜索就要出场了。这里我使用了一个 visited 变量，存放已经被访问过的结点，防止回路的产生。

/*** @Description: 通过广度优先搜索，查找好友* @param user_nodes-用户的结点；user_id-给定的用户ID，我们要为这个用户查找好友* @return void*/
public static void bfs(Node[] user_nodes, int user_id) {  if (user_id > user_nodes.length) return; // 防止数组越界的异常  Queue<Integer> queue = new LinkedList<Integer>(); // 用于广度优先搜索的队列  queue.offer(user_id); // 放入初始结点 HashSet<Integer> visited = new HashSet<>(); // 存放已经被访问过的结点，防止回路 visited.add(user_id);  while (!queue.isEmpty()) { int current_user_id = queue.poll(); // 拿出队列头部的第一个结点 if (user_nodes[current_user_id] == null) continue;  // 遍历刚刚拿出的这个结点的所有直接连接结点，并加入队列尾部 for (int friend_id : user_nodes[current_user_id].friends) { if (user_nodes[friend_id] == null) continue; if (visited.contains(friend_id)) continue; queue.offer(friend_id); visited.add(friend_id); // 记录已经访问过的结点 user_nodes[friend_id].degree = user_nodes[current_user_id].degree + 1; // 好友度数是当前结点的好友度数再加1 System.out.println(String.format("	%d度好友：%d", user_nodes[friend_id].degree, friend_id)); } }  }

需要注意的是，这里用户结点之间的边是随机生成的，所以每次结果会有所不同。如果想重现固定的结果，可以从某个文件加载用户之间的关系。