深度优先搜索与广度优先搜索

Posted 2021-04-11 WadeLearnsToCode

I See The Light.mp3 From WadeLearnsToCode 00:00 03:44

图的遍历是指从图的某一顶点出发，按照某种搜索方式沿着图中所有的顶点访问一次且仅访问一次。二叉树相比于图来说，是弱化的图。

深度优先搜索与广度优先搜索是常用的对图进行遍历的算法。

一、深度优先搜索

深度优先遍历相当于二叉树的x序遍历。

所谓深度优先搜索，是从图中的一个顶点出发，每次遍历当前访问顶点的临界点，一直到访问的顶点没有未被访问过的临界点为止。然后采用依次回退的方式，查看来的路上每一个顶点是否有其它未被访问的临界点。访问完成后，判断图中的顶点是否已经全部遍历完成，如果没有，以未访问的顶点为起始点，重复上述过程。

假如有上述的无向图，采用深度优先算法遍历这个图的过程为：

1. 首先任意找一个未被遍历过的顶点，例如从V1开始，由于V1率先访问过了，所以，需要标记V1的状态为访问过；

2. 然后遍历V1的邻接点，例如访问V2，并做标记，然后访问V2的邻接点，例如V4（做标记），然后V8，然后V5；

3. 当继续遍历V5的邻接点时，根据之前做的标记显示，所有邻接点都被访问过了。此时，从V5回退到V8 ，看V8是否有未被访问过的邻接点，如果没有，继续回退到V4，V2 ，V1；

4. 通过查看V1，找到一个未被访问过的顶点V3，继续遍历，然后访问V3 邻接点V6，然后V7；

5. 由于V7 没有未被访问的邻接点，所有回退到V6 ，继续回退至V3 ，最后到达V1 ，发现没有未被访问的；

6. 最后一步需要判断是否所有顶点都被访问，如果还有没被访问的，以未被访问的顶点为第一个顶点，继续依照上边的方式进行遍历。

经过上述流程，我们可以得到上述的图的深度优先遍历结果：

V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7

根据上面的描述，我们可以看得出来，深度优先搜索是一个递归的算法。即“找到一条路先走到黑”。

二、广度优先搜索

广度优先遍历则相当于二叉树的层次遍历。指从图中的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。最后还需要做的操作就是查看图中是否存在尚未被访问的顶点，若有，则以该顶点为起始点，重复上述遍历的过程。

仍然以这张图为例子：

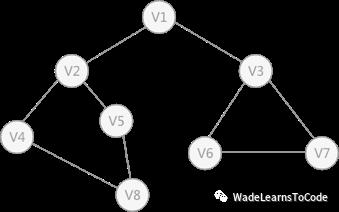
假设V1作为起始点，遍历其所有的邻接点V2和V3，以V2为起始点，访问邻接点V4和V5，以V3为起始点，访问邻接点V6、V7，以V4为起始点访问V8 ，以 V5为起始点，由于 V5 所有的起始点已经全部被访问，所有直接略过，V6 和 V7也是如此。以V1为起始点的遍历过程结束后，判断图中是否还有未被访问的点，由于图1中没有了，所以整个图遍历结束。遍历顶点的顺序为：

经过上述流程，我们可以得到上述的图的深度优先遍历结果：

V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> V8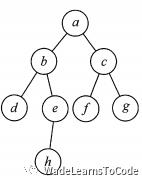

即一层一层地遍历。 类比与二叉树的层序遍历。 正因为其是一种分层的查找，每走一步都会访问一批顶点，不像深度优先搜索那样有回退的过程，所以它必然不是一个递归的算法，广度优先遍历需要辅助队列 。

三、代码实战

假设我们以下面的图为例：

就这个图而言，如果我们采用邻接矩阵来存储，我们可以得到如下的邻接矩阵：

a: 0, 1, 1, 0, 0, 0, 0, 0b: 1, 0, 0, 1, 1, 0, 0, 0c: 1, 0, 0, 0, 0, 1, 1, 0d: 0, 1, 0, 0, 0, 0, 0, 0e: 0, 1, 0, 0, 0, 0, 0, 1f: 0, 0, 1, 0, 0, 0, 0, 0g: 0, 0, 1, 0, 0, 0, 0, 0h: 0, 0, 0, 0, 1, 0, 0, 0

来看一下深度优先遍历和广度优先遍历的代码：

/*common.h*/

/*common.h*/#pragma once#include <vector>using namespace std;const char BIAS = 'a';int FirstNeighbor(const vector<vector<bool>> &vec, int u);int NextNeighbor(const vector<vector<bool>> &vec, int u, int w);

/*common.cpp */

/*common.cpp*/#include "common.h"int FirstNeighbor(const vector<vector<bool>> &vec, int u){ int sln; for(sln = 0; sln < vec.size() && vec[u].at(sln) == 0; sln++); return sln >= vec.size() ? -1 : sln;}int NextNeighbor(const vector<vector<bool>> &vec, int u, int w){ int sln = w + 1; for(; sln < vec.size() && vec[u].at(sln) == 0; sln++); return sln >= vec.size() ? -1 : sln;}

/*DFS.h*/

/*DFS.h*/#pragma once#include <iostream>#include "common.h"using namespace std;void DFSHelper(const vector<vector<bool>> &vec, int u, vector<bool>& visited);void DFS(const vector<vector<bool>> &vec, int u);

/*DFS.cpp*/

/*DFS.cpp*/#include "DFS.h"void DFSHelper(const vector<vector<bool>> &vec, int u, vector<bool>& visited){ cout << char(u + BIAS) << ' '; visited[u] = true; for(auto w = FirstNeighbor(vec, u); w >= 0; w = NextNeighbor(vec, u, w)) if(!visited[w]) DFSHelper(vec, w, visited);}void DFS(const vector<vector<bool>> &vec, int u){ vector<bool> visited(vec.size(), false); for(int i = u; i < vec.size(); i++) if(!visited[i]) DFSHelper(vec, i, visited);}

/* BFS.h */

/*BFS.h*/#pragma once#include <iostream>#include "common.h"void BFSHelper(const vector<vector<bool>> &vec, int u, vector<bool>& visited);void BFS(const vector<vector<bool>> &vec, int u);

/*BFS.cpp*/

/*BFS.cpp*/#include "BFS.h"#include <queue>using namespace std;void BFSHelper(const vector<vector<bool>> &vec, int u, vector<bool>& visited, queue<int> &q){ cout << char(u + BIAS) << ' '; visited[u] = true; q.push(u); while(!q.empty()) { u = q.front(); q.pop(); for(auto w = FirstNeighbor(vec, u); w >= 0; w = NextNeighbor(vec, u, w)) if(!visited[w]) { cout << char(w + BIAS) << ' '; visited[w] = true; q.push(w); } }}void BFS(const vector<vector<bool>> &vec, int u){ vector<bool> visited(vec.size(), false); queue<int> q; for(auto i = u; i < vec.size(); i++) if(!visited[i]) BFSHelper(vec, i, visited, q);}

/*main.cpp */

/*main.cpp*/#include "BFS.h"#include "DFS.h"#include <assert.h>#include <iostream>using namespace std;
int main(){ const vector<vector<bool>> vec{ {0, 1, 1, 0, 0, 0, 0, 0},  {1, 0, 0, 1, 1, 0, 0, 0},  {1, 0, 0, 0, 0, 1, 1, 0},  {0, 1, 0, 0, 0, 0, 0, 0},  {0, 1, 0, 0, 0, 0, 0, 1},  {0, 0, 1, 0, 0, 0, 0, 0},  {0, 0, 1, 0, 0, 0, 0, 0},  {0, 0, 0, 0, 1, 0, 0, 0} }; int n; while (1) { cout << "Which Vertex to Start(Between " << 0 << "~" << vec.size() - 1 << "): "; cin >> n; if (n >= vec.size()) { cout << "Invalid n" << endl; continue; } cout << "DFS: "; DFS(vec, n); cout << endl; cout << "BFS: "; BFS(vec, n); cout << endl; } return 0;}

/*CMakeLists.txt*/

cmake_minimum_required(VERSION 3.6.1)project(BFS_DFS)add_executable(BFS_DFS common.h common.cpp DFS.h DFS.cpp BFS.h BFS.cpp main.cpp)

来看一下运行结果：

针对上述图片列出的5个测试用例，我们来进行分析

比如输入3：意味着从第三个顶点，即d开始遍历

以d为起始顶点画出图：

深度遍历，显然为d->b->a->c->f->g->e->h

广度遍历，即层次遍历，显然为d->b->a->e->c->h->f->g

再来分析一个： 输入1 意味着从第1个顶点，即b开始遍历

以 b为 起始顶点画出 图：

深度遍历，显然为b->a->c->f->g->d ->e->h

广度遍历，即层次遍历，显然为b->a->d->e->c->h->f->g

参考文章

[1] http://data.biancheng.net/view/39.html

[2] https://blog.csdn.net/weixin_38391755/article/details/80380786

[3] https://blog.csdn.net/u011520181/article/details/81702460