数据结构--平衡二叉树实现
Posted 码农修仙儿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构--平衡二叉树实现相关的知识,希望对你有一定的参考价值。
就在昨天,折磨我这么长时间的平衡二叉树终于算是有了一个进步
为了验证代码的执行结果,还手算了一遍
在结果验证正确的那一刻,感觉一切都值了~~
其实我是个菜鸟,能做到这一步,只是因为很有耐心...

还记得上一篇对平衡二叉树实现的分析吗?
来,复习一下
真的是说起来容易做起来难..理论上是可以,实现起来不容易啊,成功实现了一个“增加元素”的方法,就已经想哭了
头发有没有掉我没注意,但脑细胞绝对死了一大波儿了

废话不多说,直奔主题
先说第一个问题:如何识别二叉树是否平衡?
这个理论上是很简单了:
如果所有节点的左子树和右子树的高度差都小于等于1,那么就表示二叉树平衡了.
举个栗子,如下图
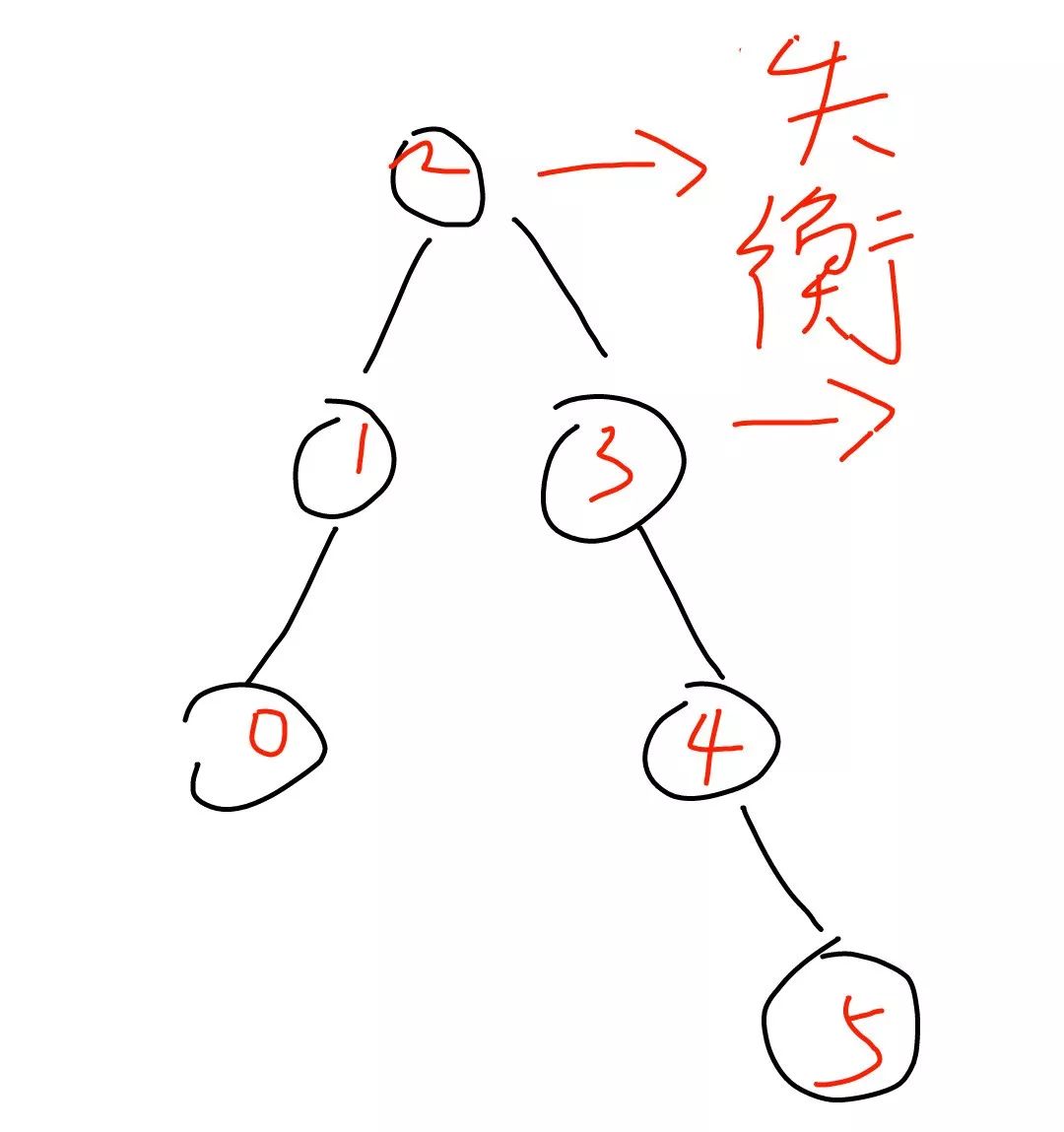
图中有两个失衡节点,2和3,所以二叉树不平衡,需要调整
在调整前要确认需要调整的失衡节点,失衡节点有两个,要调整哪个?调整深度最低的失衡节点。
明显2的深度要比3的大,所以需要调整节点3
也就是说,目前要做的就是两件事
第一,判断二叉树是否失衡,找到所有失衡节点
第二,找到需要调整的节点,从失衡节点中找到最低失衡节点
道理是这么个道理,谁都懂
但这是程序,又不是说肉眼去识别的,我该怎么找?这就涉及到程序设计了。
为了能够确认某个节点是否是失衡节点,那么我需要知道该节点的左子树高度和右子树高度
在确认了高度差之后,我还需要在失衡节点之间进行一个比较判断,所以我需要一个层级值,来表示节点深度
基于此,我的节点Node对象就出来了
1class Node<K, V> {
2 Node<K, V> parent;
3 Node<K, V> left;
4 Node<K, V> right;
5 K key;
6 V value;
7 int leftHeight;//左子树的深度
8 int rightHeight;//右子树的深度
9 int level;//从root节点为0开始,依次累加
10
11 Node(K key, V value, Node<K, V> parent) {
12 this.key = key;
13 this.value = value;
14 this.parent = parent;
15 leftHeight = 0;
16 rightHeight = 0;
17 level = 0;
18 }
19 }
借助一张图,来看下level和height的定义
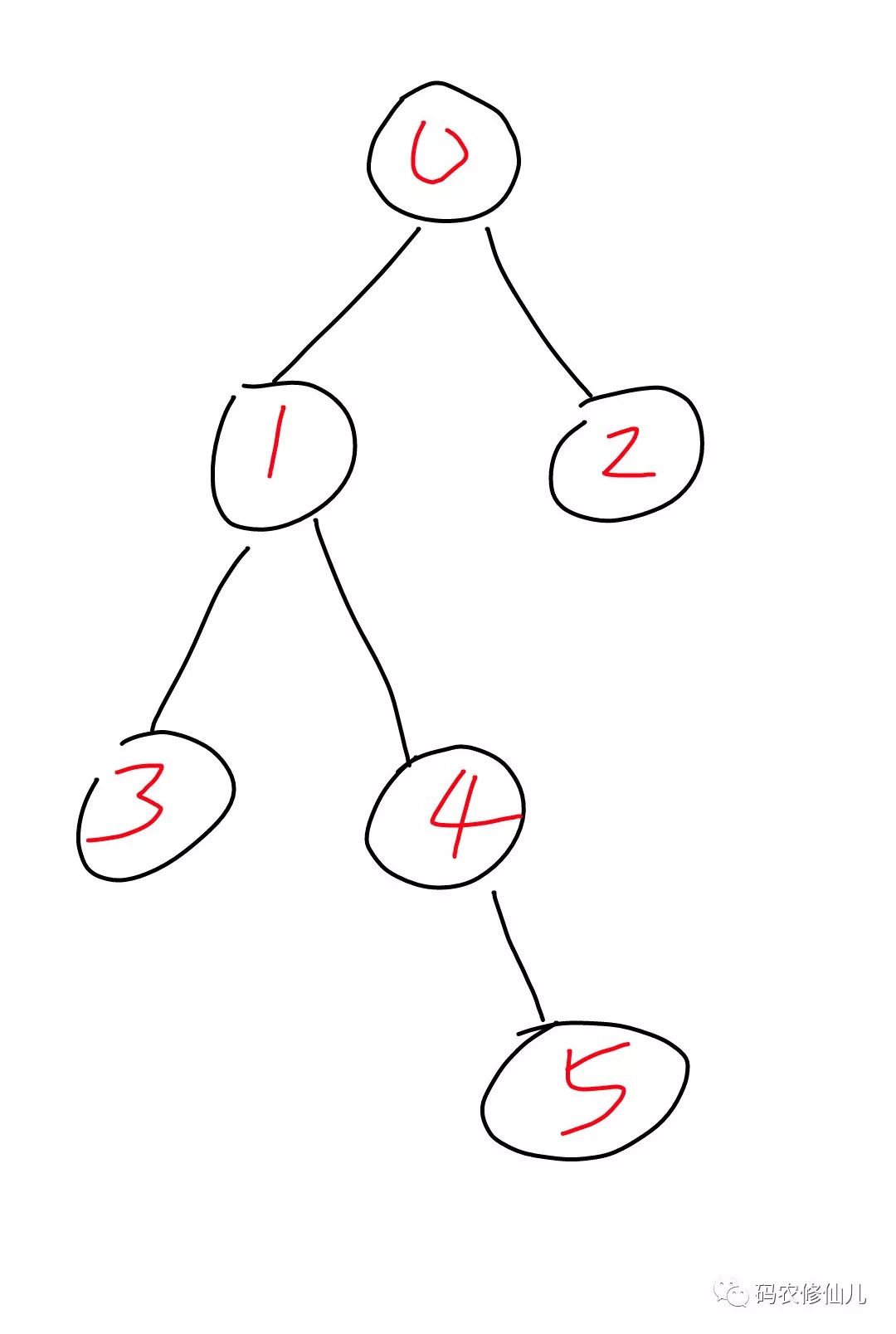
图中数字代表标号,不代表大小。
0号:level为0,leftHeight为3,rightHeight为1
1号:level为1,leftHeight为1,rightHeight为2
2号:level为1,leftHeight为0,rightHeight为0
3号:level为2,leftHeight为0,rightHeight为0
4号:level为2,leftHeight为0,rightHeight为1
5号:level为3,leftHeight为0,rightHeight为0
根据这个分析,就可以很明显的看出失衡节点是0.
那代码如何实现寻找最低失衡节点?
首先是找到左右子树差大于1的节点
再从这些失衡节点中找到level值大的那个节点
1 private Node<K, V> unbalanceNode() {
2 Node<K, V> temp = root;
3 Node<K, V> tempParent = null;
4 Node<K, V> lastBadNode = null;
5 /*
6 * 找到二叉树中的最小的节点:tempParent
7 */
8 while (temp != null) {
9 tempParent = temp;
10 temp = temp.left;
11 }
12 while (tempParent != null) {
13 /*
14 * 计算每个节点左右子树的高度差,找到失衡节点
15 */
16 int subValue = Math.abs(tempParent.leftHeight - tempParent.rightHeight);
17 if (subValue > 1 && (lastBadNode == null || lastBadNode.level < tempParent.level)) {
18 //高度差满足,并且遍历到的level是最大的,也就是位置最低
19 lastBadNode = tempParent;
20 }
21 //寻找下一个节点
22 tempParent = nextNode(tempParent);
23 }
24 return lastBadNode;
25 }
查找最低失衡节点就结束了
在查找过程中有一个方法:nextNode--寻找下一个节点
说一下nextNode的实现逻辑,也就是如何去寻找一个节点的下一个节点
首先,去寻找该节点的右子树的最小值,如果存在,那么就是该节点的下一个节点
否则,则要去遍历该节点的parent…parent,直至找到该节点存在于某个节点的左子树中,那么某个节点就是下一个节点
找到最低失衡节点之后,接下来就是调整了
1private void adjustTree(Node<K, V> parent) {
2 Node<K, V> unBalanceNode = unbalanceNode();
3 while (unBalanceNode != null) {
4 System.out.println("unBalanceNode:" + unBalanceNode);
5 //如果unBalanceNode is null 二叉树中没有失衡节点,所以不需要进行旋转
6 if ((unBalanceNode.leftHeight - unBalanceNode.rightHeight) > 1) {
7 rotateRight(unBalanceNode);
8 } else if ((unBalanceNode.leftHeight - unBalanceNode.rightHeight) < -1) {
9 rotateLeft(unBalanceNode);
10 }
11 unBalanceNode = unbalanceNode();
12 }
13}
如何进行调整?这又是一个值得考虑的问题了,二叉树的调整涉及到的是旋转问题
如果最低失衡节点的leftHeight > rightHeight,那么就表示左子树层级比较多,所以把左子树向右旋转,即调用rotateRight方法进行左子树右旋
反之,也就是说最低失衡节点的rightHeight > leftHeight, 那么就表示右子树层级比较多,所以把右子树左旋,即调用rotateLeft方法进行右子树左旋
在旋转结束后,还要继续判断二叉树中是否还存在失衡节点。
一个是因为失衡节点不止一个,还有一个原因是旋转后原先失衡节点可能依旧失衡
ok,好了,先是寻找到最低失衡节点,紧接着调整二叉树重新平衡了,对于二叉树的操作就完成了。
那么二叉树如何左旋和右旋的呢?
这个旋转会涉及到三个问题
节点的位置修改
节点的level修改
节点的height子树高度修改
关于”左旋和右旋时节点之间是如何替换的“这个问题,在上一文中已经写的很清楚了
如果是右子树左旋,那就是找到最低失衡节点的右子树的极小值点,来代替最低失衡节点的位置。
右子树的极小值点比右子树的所有节点都小,但却比最低失衡节点大
所以将最低失衡节点调整为极值点的左子树
既然是右子树的极小值点,那极值点必然只有右子树,没有左子树。将极值点的右子树交给极值点parent的左子树
如果是左子树右旋,那就寻找最低失衡节点的左子树的极大值点,来代替最低失衡节点的位置
左子树的极大值点比左子树的所有节点都大,但却比最低失衡节点小
所以将最低失衡节点调整为极值点的右子树
既然是左子树的极大值点,那么极值点必然只有左子树,没有右子树,将极值点的左子树交给极值点parent的右子树
其实节点替换还好说,关键难点在于level和height需要调整,这个真的是要哭了
不过最终还是成功了,感恩感恩
来看下level的调整,需要调整四个部分
需要旋转的子树的极值点,exNode极值点本身level=>badNode.level
最低失衡节点badNode的level +1
最低失衡节点badNode的所有子节点的level++
极值点exNode的所有子节点的level --
1 /**
2 *
3 * @param exNode 失衡极值点,
4 * @param badNode 最低失衡节点
5 * @param isRotateLeft 是否是右子树左旋
6 */
7 private void adjustLevelWhenRotate(Node<K, V> exNode, Node<K, V> badNode, boolean isRotateLeft) {
8
9 //调用必须是在调整之前
10 exNode.level = badNode.level;
11 badNode.level += 1;
12
13 //isRotateLeft为true表示右子树左旋,代表失衡节点的左子树需要调整
14 List<Node<K, V>> leftTree = iteratorTree(isRotateLeft, badNode);
15 for (Node<K, V> node : leftTree) {
16 if (node != null) {
17 node.level++;
18 }
19 }
20
21 //右子树中的最小值exNode为极值点,所以exNode只有右子树
22 List<Node<K, V>> ex_leftTree = iteratorTree(!isRotateLeft, exNode);
23 for (Node<K, V> node : ex_leftTree) {
24 if (node != null) {
25 node.level--;
26 }
27 }
这个level的调整,自己画个二叉树的图就清晰了。
因为极值点代替了失衡节点,所以极值点的level就等于失衡节点的level
最低失衡节点因为旋转的原因,一定会成为极值点的子树,也就是相对于原先的位置,层级又往下移。所以level+1
当然最低失衡节点的所旋转的子树,对应节点的位置是和badNode的变化保持一致的,所以level+1
最后就是极值点的子树中,所有节点位置上移,所以level-1
调整完level之后,就是height的调整了
需要调整哪些节点的height?
极值点的height肯定需要调整
最低失衡节点的height也需要调整
极值点的parent的height需要调整
极值点的parent.parent..都可能需要调整
这个还是需要区分左旋和右旋的
1if (exNode != exNode.parent.right) {
2 exNode.parent.leftHeight = exNode.rightHeight;
3} else {
4 exNode.parent.rightHeight = exNode.rightHeight;
5 }
6
7 Node<K, V> child = exNode.parent;
8 Node<K, V> parent = child.parent;
9 while (parent != null) {
10 if (child == parent.left) {
11 parent.leftHeight = Math.max(child.leftHeight, child.rightHeight) + 1;
12 } else {
13 parent.rightHeight = Math.max(child.leftHeight, child.rightHeight) + 1;
14 }
15
16 child = parent;
17 parent = child.parent;
18 }
19
20 exNode.leftHeight = badNode.leftHeight + 1;
21 exNode.rightHeight = badNode.rightHeight;
22 badNode.rightHeight = 0;
如果是右子树左旋,极值点是右子树的极小值点,调整代码如上图所示
对于极值点的parent来说,只需要调整包含极值点的子树的高度。那就是极值点的右子树的高度
在调整了parent节点之后,会不会对parent…parent…产生影响呢?
不管有没有影响,直接把child的高度给parent。所以parent的height有可能会修改,也可能不会
紧接着,极值点的左子树目前是失衡节点了,所以左子树高度就是失衡节点的左子树高度+1.极值点右子树高度就是失衡节点原先的右子树高度
最后,因为是右子树左旋,失衡节点的右子树被清空,所以失衡节点的右子树高度置为0
同理,可以推出左子树右旋时高度的调节
至此二叉树调整结束,回归平衡
接下来你可以开始增加元素了,也就是实现put方法
在插入之前,要明确几点
第一,插入之前二叉树一定是平衡的
第二,新插入的节点,如果是非root节点,那么一定是叶子节点
所以插入分为以下三步
1,首先执行插入操作,分三种情况
<1>若插入的为root节点,那么二叉树不需要进行任何调整
<2>若插入的是已存在的节点,那么二叉树只需要更新value,也不需要调整
<3>若插入的是新的节点,那就表示插入的一定是叶子节点,那么二叉树需要调整
2,调整height和level
<1>level,由root到根节点 ++
<2>height,由根节点到root修改(increaseHeight方法)
3,调整二叉树平衡,需要根据平衡二叉树的第四条性质,对二叉树进行相应的调整
代码就不贴了,难点也不在这儿。只要搞明白了如何寻找最低失衡节点,以及寻找到之后如何旋转二叉树,那么这儿的问题对你来说不算难点
具体代码实现可以去看gitHub
代码有很多注释,以及代码实现过程。点击阅读原文可以看到源码
最后的最后,分享转发一波儿呗~

以上是关于数据结构--平衡二叉树实现的主要内容,如果未能解决你的问题,请参考以下文章