平衡二叉树的定义及基本操作(查找插入删除)及代码实现
Posted 薛定谔的猫ovo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了平衡二叉树的定义及基本操作(查找插入删除)及代码实现相关的知识,希望对你有一定的参考价值。
文章目录
平衡二叉树的定义
为了避免树的高度增长过快,降低二叉排序树的性能,我们规定在插入和删除二叉树结点时,要保证在任意结点的左、右子树高度差的绝对值不超过1,将这样的树称为平衡二叉树(Balanced Binary Tree),简称平衡树(AVL)。此外,AVL树又称为高度平衡的二叉查找树。
定义结点左子树与右子树的高度差为该结点的平衡因子,则平衡二叉树结点的平衡因子的值只可能是-1,0或1 。
平衡二叉树可定义为:
或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的高度差的绝对值不超过1。

平衡二叉树的结点类型描述:
typedef struct AVLNode{
int data; //数据域
int bf; //平衡因子
struct AVLNode *lchild, *rchild; //指针域
}AVLNode, *AVLTree;
平衡二叉树的查找
平衡二叉树上进行查找的过程与二叉排序树相同,详细完整代码请参照二叉排序树的定义及基本操作(构造、查找、插入、删除)递归及非递归算法。因此,在查找过程中,与给定值进行比较的关键字个数不超过树的深度。
可以证明,含有n个结点的平衡二叉树的最大深度为O(log2n),因此平衡二叉树的平均查找长度为O(log2n)。
平衡二叉树的平衡旋转
二叉排序树保证平衡的基本思想如下:
每当在二叉排序树中插入(或删除)一个结点时,首先检查其插入路径上的结点是否因为此次操作导致了不平衡。若导致了不平衡,则先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A,再对以A为根的子树,在保持二叉排序树特性的前提下,调整各结点的位置关系,使之重新达到平衡。
一般可将失去平衡后进行调整的规律归纳为下列四种情况:LL平衡旋转,RR平衡旋转,LR平衡旋转,RL平衡旋转。
LL平衡旋转(右单旋转)
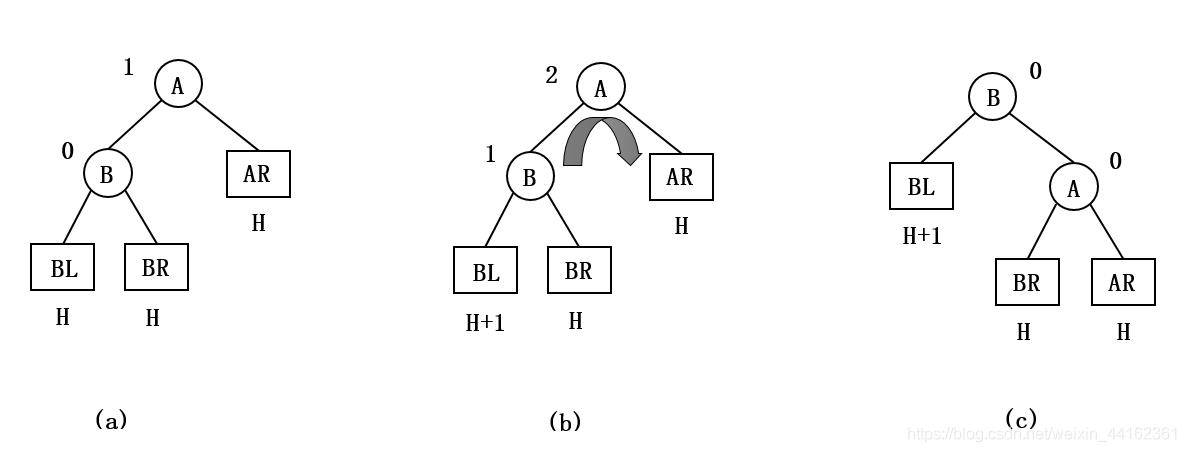
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致了以A为根的子树失去平衡。
需要一次向右的旋转操作:将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
如下图所示,结点旁的数值代表结点的平衡因子,方块表示相应结点的子树,方块下的数值代表该子树的高度,以下相同,不再赘述。
实现代码:
void Rotate_LL(AVLNode *&p){
AVLNode *s = p; //要右旋转的结点
p = s->lchild;
s->lchild = p->rchild; //卸掉p右边的负载
p->rchild = s; //右单旋, p成为新根
p->bf = 0;
s->bf = 0;
}
RR平衡旋转(左单旋转)
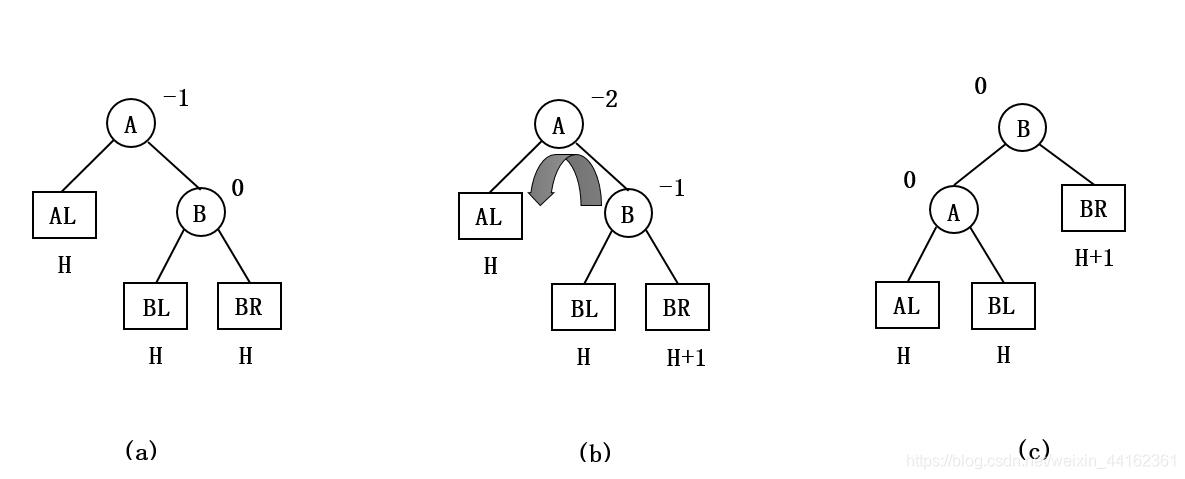
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡。
需要一次向左的旋转操作:将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树作为A结点的右子树。如下图所示:
实现代码:
void Rotate_RR(AVLNode *&p){
AVLNode *s = p; //要左旋转的结点
p = s->rchild; //卸掉p左边的负载
s->rchild = p->lchild;
p->lchild = s; //左单旋, p成为新根
p->bf = 0;
s->bf = 0;
}
LR平衡旋转(先左后右双旋转)
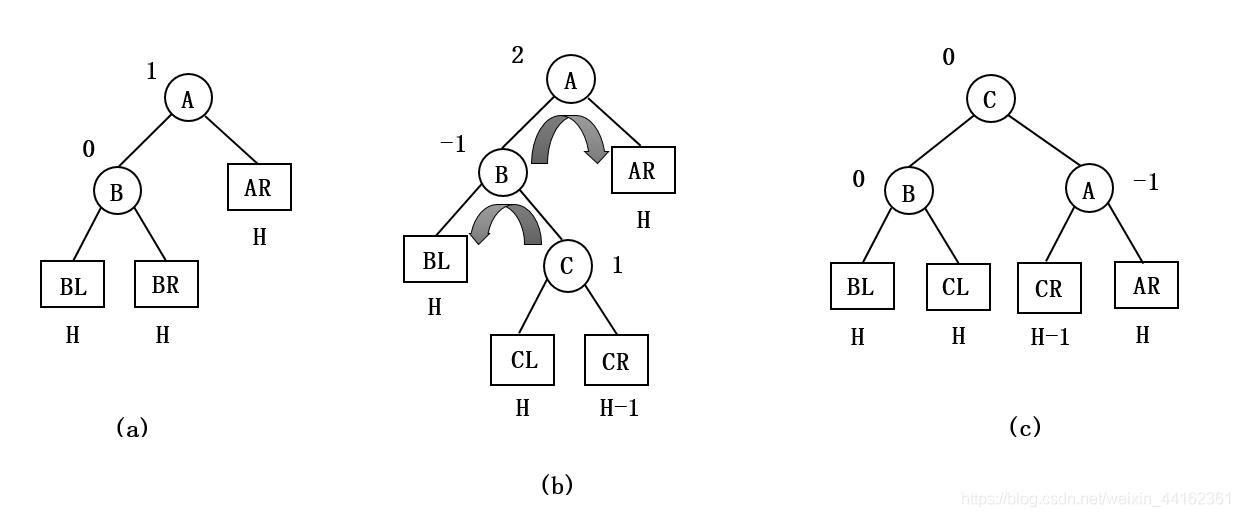
由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡。
需要进行两次旋转操作:先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置。如下图所示:
【注意】LR和RL旋转时,新结点究竟是插入C的左子树还是插入C的右子树均不影响旋转过程,在下面的图中以插入C的左子树中为例。
实现代码:
void Rotate_LR(AVLNode *&p){
AVLNode *sr = p, *sl = sr->lchild;
p = sr->rchild; //p成为新根
sl->rchild = p->lchild; //卸掉p左边的负载
p->lchild = sl;
sr->lchild = p->rchild; //卸掉p右边的负载
p->rchild = sr;
if(p->bf == 1){ //原p左子树高
sl->bf = 0;
sr->bf = -1;
}else if(p->bf == -1){ //原p右子树高
sl->bf = 1;
sr->bf = 0;
}else{ //原p两子树同高
sl->bf = 0;
sr->bf = 0;
}
p->bf = 0;
}
RL平衡旋转(先右后左双旋转)
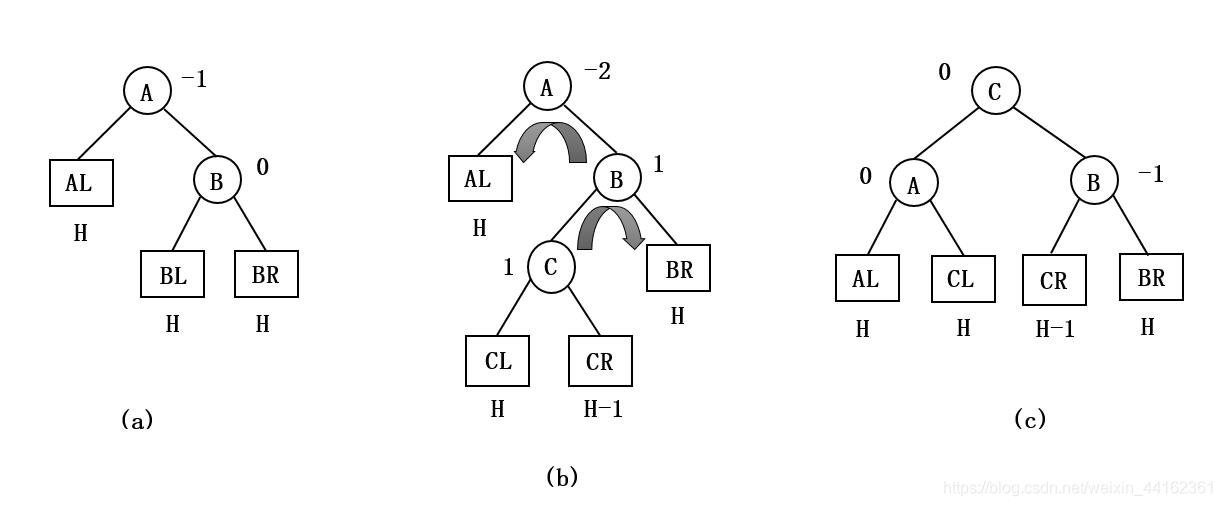
由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡。
需要进行两次旋转操作:先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。如下图所示:
实现代码:
void Rotate_RL(AVLNode *&p){
AVLNode *sl = p, *sr = p->rchild; //p成为新根
p = sr->lchild;
sr->lchild = p->rchild; //卸掉p右边的负载
p->rchild = sr;
sl->rchild = p->lchild; //卸掉p左边的负载
p->lchild = sl;
if(p->bf == 1){ //原p左子树高
sl->bf = 0;
sr->bf = -1;
}else if(p->bf == -1){ //原p右子树高
sl->bf = 1;
sr->bf = 0;
}else{ //原p两子树同高
sl->bf = 0;
sr->bf = 0;
}
p->bf = 0;
}
平衡二叉树的插入
平衡二叉树的插入过程前半部分与二叉排序树相同,但是在新结点插入后,若造成查找路径上的某个结点不再平衡,则需要做出相应的调整。
在新结点作为叶结点插入后,必须从插入位置沿到根结点的路径回溯,检查在此路径上的结点是否变得不平衡。若是,则找出其中的最小不平衡子树,在保持二叉查找树特性的情况下,调整最小不平衡子树中结点之间的关系,使之达到新的平衡;否则,本次插入结束。
所谓最小不平衡子树,是指插入后在所有失去平衡性的结点中,以离插入结点最近的结点作为根的那棵子树,这个根结点一定处于在查找插入位置时所经过的路径上。
然后,在找到的最小不平衡子树上识别平衡旋转类型(LL、RR、LR、RL),做完平衡旋转后,本次插入即可结束。
平衡二叉树的删除
平衡二叉树的删除过程与二叉查找树类似。不同之处在于:若删除后破坏了AVL树的高度平衡性,还需要做平衡旋转。
<1>如果被删除结点*p有两个子女。首先查找*p在中序下的直接前驱*q(同样可以查找中序下的直接后继)。再把结点*q的内容传送给结点*p,把问题转移到删除最多只有一个子女的结点*q,把结点*q当作被删结点*p。(就是二叉排序树中的删除情况3的过程)
<2>如果被删除结点*p只有一个子女*q,可以把*p的双亲*f中原来指向*p的指针指到*q;(二叉排序树中的删除情况2)
<3>如果被删除结点*p没有子女,*p的双亲*f的相应指针置为NULL。(二叉排序树中的删除情况1)然后将原来以结点*f为根的子树的高度减1,并沿着*f到根的路径方向追踪高度变化对路径上各个结点的影响。
若*p是*f的左子女,则*f的左子树高度降低,平衡因子减1;若*p是*f的右子女,则*f的右子树高度降低,平衡因子加1。
根据修改后的*f的平衡因子,按三种情况处理:1.结点*f的平衡因子原来为0;2.结点*f的平衡因子原不为0,且较高子树的高度降低;3.结点*f的平衡因子原来不为0,且较矮子树的高度降低。
被删除结点的双亲原平衡因子为0
结点*f的平衡因子原来为0,在它的左子树或右子树高度降低后,它的平衡因子改为1或-1。由于以*f为根的子树高度没有改变,从*f到根结点的路径上的所有结点不需要调整。如下图所示:

被删除结点的双亲原平衡因子不为0且较高子树高度降低
结点*f的平衡因子原不为0,且较高的子树的高度降低,则*p的平衡因子改为0。此时以*f为根的子树平衡,但其高度减1。为此需要继续上溯,考察结点*f的双亲的平衡状态。如下图所示:
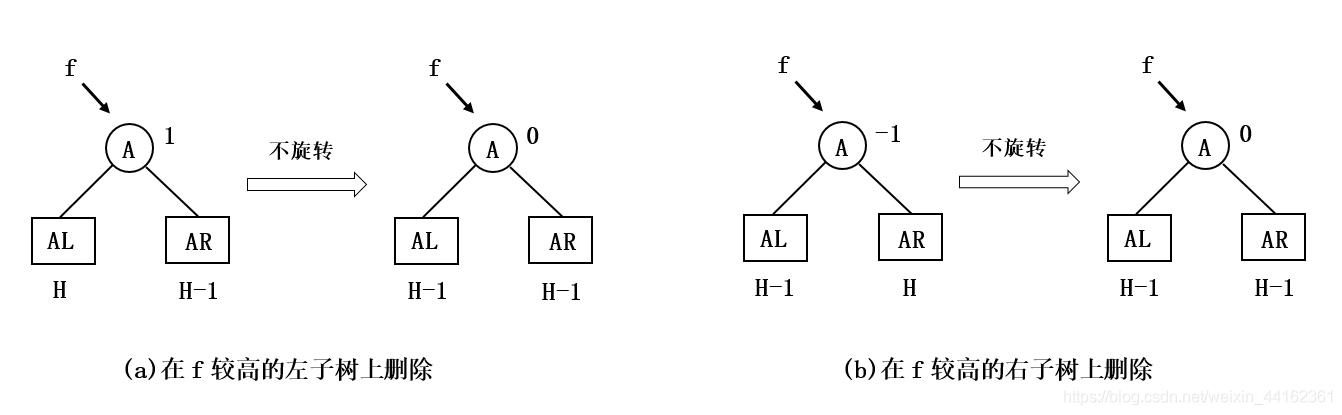
被删除结点的双亲原平衡因子不为0且较矮子树高度降低
结点*f的平衡因子原不为0,且较矮的子树的高度降低,则在结点*f处发生不平衡。需要进行平衡旋转来恢复平衡。
令*f的较高的子树的根为*q(该子树的高度未发生变化),根据*q的平衡因子,有以下三种平衡化操作。
<一> *q的平衡因子为0
如果*q的平衡因子为0,执行一个单旋操作来恢复结点*f的平衡,如下图所示:
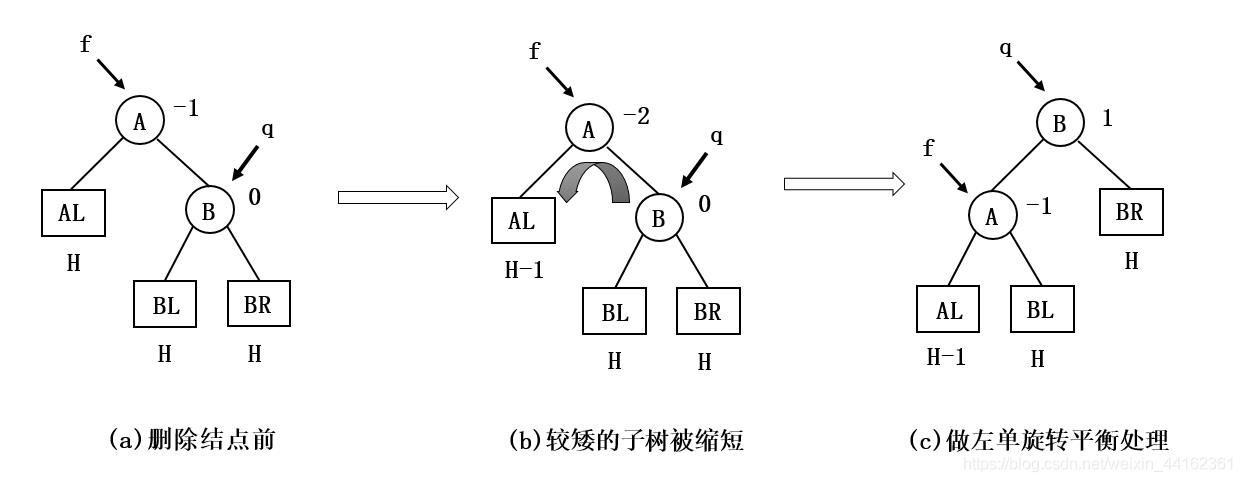
上图是左单旋转的例子,右单旋转的情形可以对称的处理。由于平衡旋转后以*q为根的子树的高度没有发生改变,此时可以结束平衡化处理过程。
<二> *q的平衡因子与双亲*f的平衡因子正负号相同
如果*q的平衡因子与双亲*f的平衡因子正负号相同,则执行一个单旋转来恢复平衡,结点*f和*q的平衡因子均改为0,如下图所示:
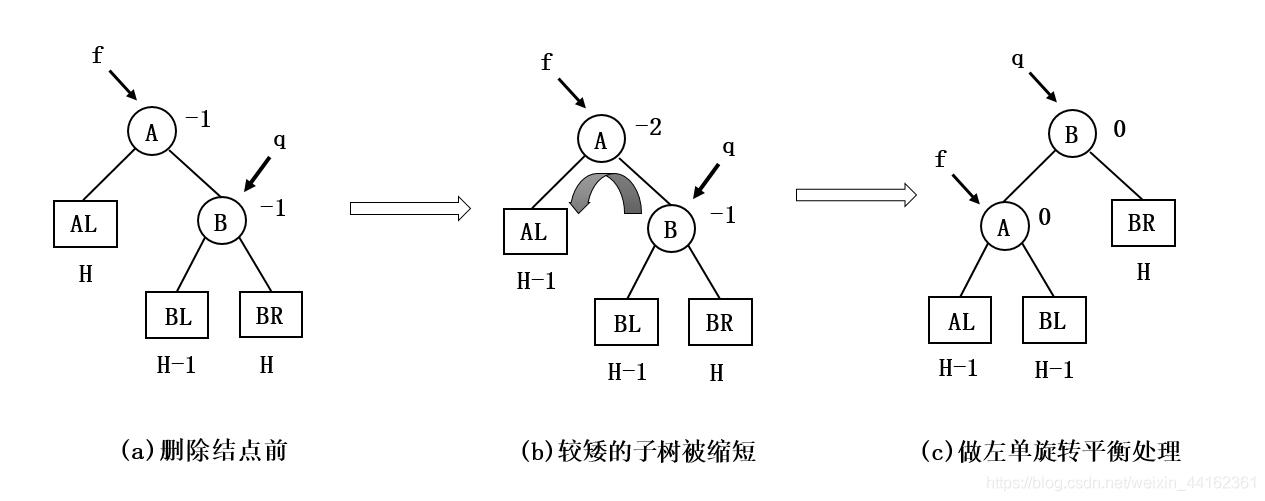
图中是做单旋转的例子,右单旋转的情形可以对称的处理。由于经过平衡旋转后结点*q的子树高度降低1,故需要继续沿插入路径上溯考察结点*q的双亲的平衡状态。
<三> *q的平衡因子与双亲*f的平衡因子正负号相反
如果*f与*q的平衡因子正负号相反,则执行一个双旋转来恢复平衡,如下图所示:
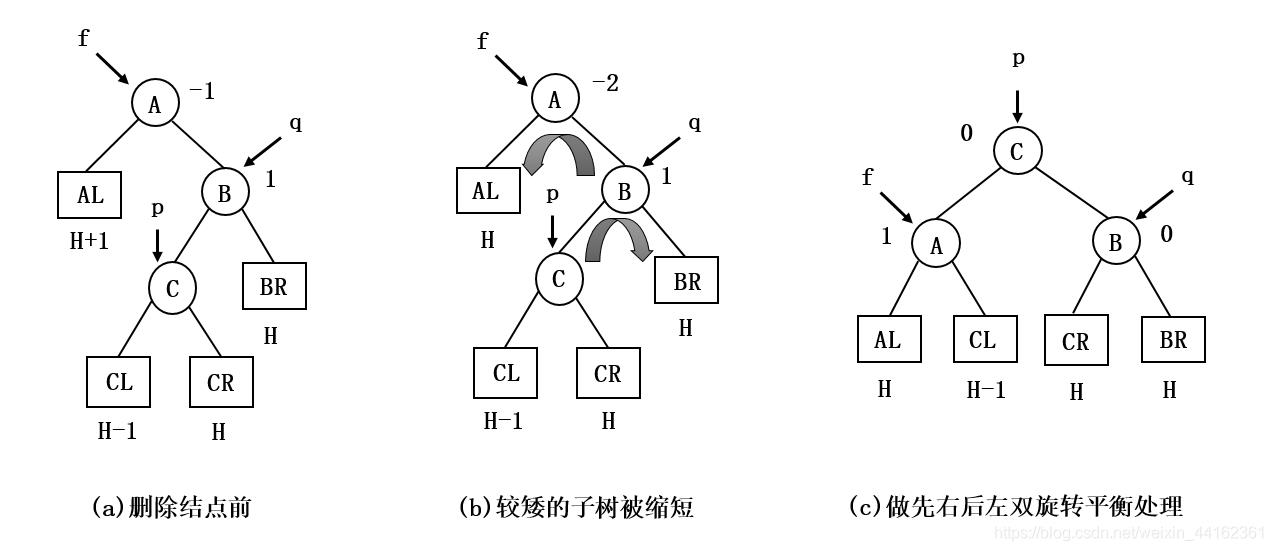
先围绕*q转再围绕*f转。新的根结点的平衡因子置为0,其他结点的平衡因子相应的调整。还需要上溯考察它的双亲,继续向上层进行平衡化工作。
最极端的情形是:如果回溯路径上每个结点都需要平衡旋转,可能导致AVL树的高度降低,甚至原来的根结点都可能旋转下去,被旋转上来的结点替代。
以上是关于平衡二叉树的定义及基本操作(查找插入删除)及代码实现的主要内容,如果未能解决你的问题,请参考以下文章