16、toy数据集上不同聚类算法的比较
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了16、toy数据集上不同聚类算法的比较相关的知识,希望对你有一定的参考价值。
参考技术A 16、toy数据集上不同聚类算法的比较import time
import warnings
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets, mixture
from sklearn.neighbors import kneighbors_graph
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
np.random.seed(0)
# 生成数据集
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5,
noise=.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None
# 各向异性分布数据
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
# 变方差斑点
varied = datasets.make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
# 设置群集参数
plt.figure(figsize=(9 * 2 + 3, 12.5))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05,
hspace=.01)
plot_num = 1
default_base = 'quantile': .3,
'eps': .3,
'damping': .9,
'preference': -200,
'n_neighbors': 10,
'n_clusters': 3,
'min_samples': 20,
'xi': 0.05,
'min_cluster_size': 0.1
datasets = [
(noisy_circles, 'damping': .77, 'preference': -240,
'quantile': .2, 'n_clusters': 2,
'min_samples': 20, 'xi': 0.25),
(noisy_moons, 'damping': .75, 'preference': -220, 'n_clusters': 2),
(varied, 'eps': .18, 'n_neighbors': 2,
'min_samples': 5, 'xi': 0.035, 'min_cluster_size': .2),
(aniso, 'eps': .15, 'n_neighbors': 2,
'min_samples': 20, 'xi': 0.1, 'min_cluster_size': .2),
(blobs, ),
(no_structure, )]
for i_dataset, (dataset, algo_params) in enumerate(datasets):
# 使用特定于数据集的值更新参数
params = default_base.copy()
params.update(algo_params)
X, y = dataset
# 规范化数据集以方便参数选择
X = StandardScaler().fit_transform(X)
# 均值漂移估计带宽
bandwidth = cluster.estimate_bandwidth(X, quantile=params['quantile'])
# 结构化Ward的连通矩阵
connectivity = kneighbors_graph(
X, n_neighbors=params['n_neighbors'], include_self=False)
# 使连通对称
connectivity = 0.5 * (connectivity + connectivity.T)
# 创建群集对象
ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True)
two_means = cluster.MiniBatchKMeans(n_clusters=params['n_clusters'])
ward = cluster.AgglomerativeClustering(
n_clusters=params['n_clusters'], linkage='ward',
connectivity=connectivity)
spectral = cluster.SpectralClustering(
n_clusters=params['n_clusters'], eigen_solver='arpack',
affinity="nearest_neighbors")
dbscan = cluster.DBSCAN(eps=params['eps'])
optics = cluster.OPTICS(min_samples=params['min_samples'],
xi=params['xi'],
min_cluster_size=params['min_cluster_size'])
affinity_propagation = cluster.AffinityPropagation(
damping=params['damping'], preference=params['preference'])
average_linkage = cluster.AgglomerativeClustering(
linkage="average", affinity="cityblock",
n_clusters=params['n_clusters'], connectivity=connectivity)
birch = cluster.Birch(n_clusters=params['n_clusters'])
gmm = mixture.GaussianMixture(
n_components=params['n_clusters'], covariance_type='full')
clustering_algorithms = (
('小型化', two_means),
('亲和传播', affinity_propagation),
('平均数移位', ms),
('光谱聚类', spectral),
('Ward', ward),
('凝聚剂聚类', average_linkage),
('DBSCAN', dbscan),
('OPTICS', optics),
('Birch', birch),
('高斯混合物', gmm)
)
for name, algorithm in clustering_algorithms:
t0 = time.time()
# 捕获与kneighs_graph相关的警告
with warnings.catch_warnings():
warnings.filterwarnings(
"ignore",
message="the number of connected components of the " +
"connectivity matrix is [0-9]1,2" +
" > 1. Completing it to avoid stopping the tree early.",
category=UserWarning)
warnings.filterwarnings(
"ignore",
message="Graph is not fully connected, spectral embedding" +
" may not work as expected.",
category=UserWarning)
algorithm.fit(X)
t1 = time.time()
if hasattr(algorithm, 'labels_'):
y_pred = algorithm.labels_.astype(np.int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a',
'#f781bf', '#a65628', '#984ea3',
'#999999', '#e41a1c', '#dede00']),
int(max(y_pred) + 1))))
# 为异常值添加黑色(如果有)
colors = np.append(colors, ["#000000"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'),
transform=plt.gca().transAxes, size=15,
horizontalalignment='right')
plot_num += 1
plt.show()
k-means聚类算法原理简析
k-means聚类算法原理简介
概要
K-means算法是最普及的聚类算法,也是一个比较简单的聚类算法。
算法接受一个未标记的数据集,然后将数据聚类成不同的组,同时,k-means算法也是一种无监督学习。
算法思想
k-means算法的思想比较简单,假设我们要把数据分成K个类,大概可以分为以下几个步骤:
1.随机选取k个点,作为聚类中心;
2.计算每个点分别到k个聚类中心的聚类,然后将该点分到最近的聚类中心,这样就行成了k个簇;
3.再重新计算每个簇的质心(均值);
4.重复以上2~4步,直到质心的位置不再发生变化或者达到设定的迭代次数。
算法流程图解
下面我们通过一个具体的例子来理解这个算法(我这里用到了Andrew Ng的机器学习教程中的图):
假设我们首先拿到了这样一个数据,要把它分成两类:
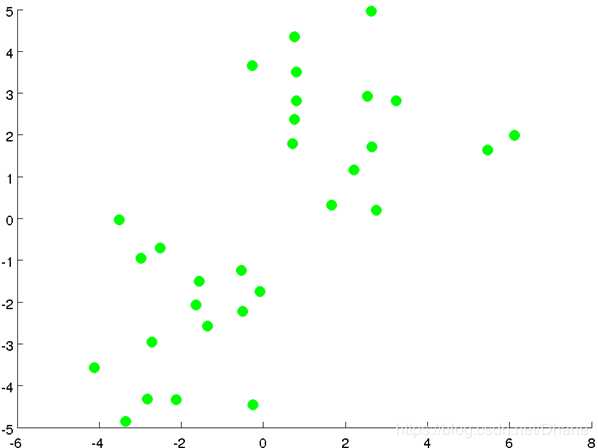
我们人眼当然可以很快的分辨出来,可以在两个聚类间找到一条合理的分界线,
那么用k-means算法来解决这个问题会是怎样的呢?
首先我们随机选取两个点作为聚类中心(因为已经明确是分为两类):
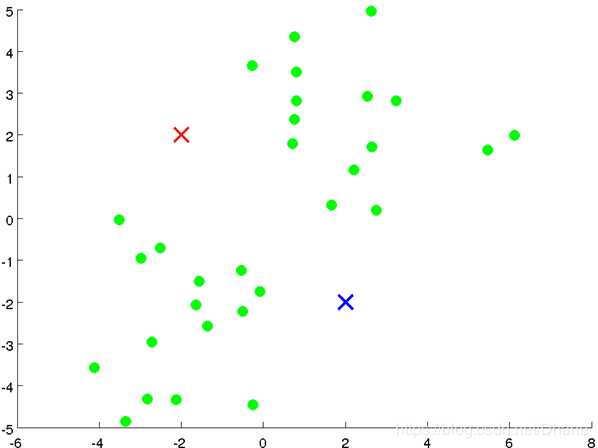
接下来就可以开始计算每个点到红点和蓝点的距离了,离红点近就标记为红色,离蓝点近就标记为蓝色。结果为下图:
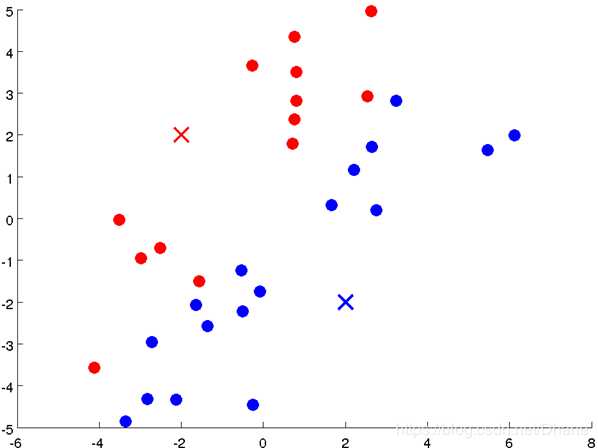
很明显,这样完全不是我们想要的结果,接下来我们进行第三步,重新计算聚类中心的位置。

红X和蓝X都向中间靠拢了一点。
我们可以看到,聚类中心发生改变后,其他点离两个聚类中心的距离也跟随着发生了变化。
然后我们重复第二步,根据每个点到两个聚类中心的距离远近来进行重新分类,
离红X近的归为红类,离蓝X近的归为蓝类。
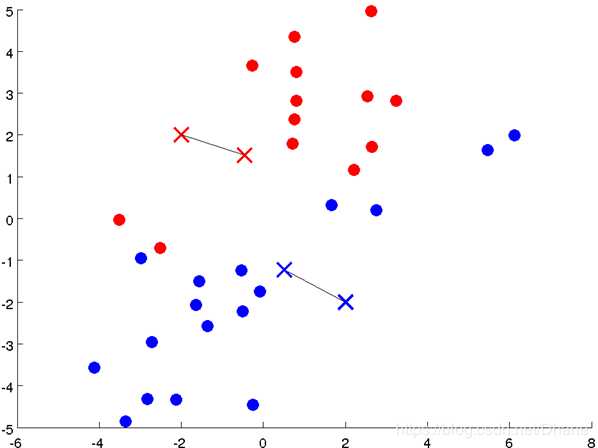
之前站错了队伍的一些点重新进行了调整,现在的分类离我们的目标越来越近了,
但还没有达到最佳的分类效果。接下来继续重复上面的步骤,重新计算聚类中心的位置,
再重新分类,不断迭代,直至聚类中心的位置不再变化(变化范围达到设定值)或达到迭代次数为止。
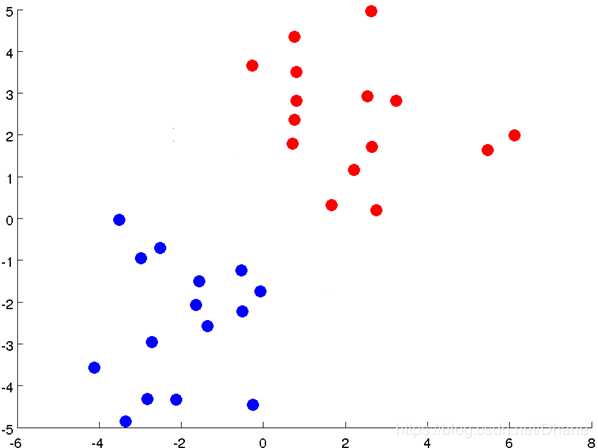
这样我们就利用k-means算法把这个数据很好的分为两类啦。
我们可以看到,在整个过程中,我们都没有去监督算法,告诉他具体是分错了还是对了,
只是在开始的时候告诉他要把这个数据分成多少类,然后后面的操作都是由他自己完成,
完全没有人为的让他进行分类的学习,也没有帮助他纠正错误,所以k-means算法也是一种无监督学习方法。
相信看到这里你对k-means算法的原理也有了一个大概的了解啦。
代价函数(Distortion function)
要是k-means最后的分类结果最好,也就是要是K-均值最小化,
是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,
因此我们可以设计 K-均值的代价函数(又称 畸变函数 Distortion function)为:
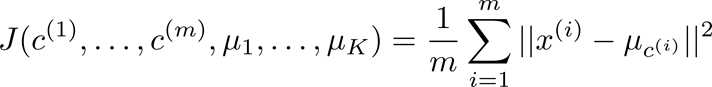
其中μ c (i)代表与 x (i) 最近的聚类中心点。
我们的的优化目标也就是要找出使得代价函数最小的 c (1) ,c (2) ,…,c (m) 和μ 1 ,μ 2 ,…,μ k 。
我们再回顾一下刚才给出的 K-means算法的迭代过程,我们知道,第一个步骤(根据聚类中心分类)
是用于减小 c (i) 引起的代价,而第二个步骤(重新定位聚类中心)则是用于减小μ i 引起的代价。
所以迭代的过程一定会是每一次迭代都在减小代价函数,如果发生迭代之后代价函数反而增加,则很可能是出现了错误。
如何选取k值
对于一个给定没有分类的数据集,最后具体应该分为多少类呢?
这确实是一个问题,比如我们前面的那个例子,通过人眼观察,很明显可以分为两类,那么我们选取K值为2,
可以得到一个比较好的聚类结果。那如果K选择3或者其他值行不行呢?当然也可以。
比如下图,有一个数据经过统计之后发现随着K值的增加其畸变函数在不断变小,但是我们发现在k=3时,
畸变函数随着k值变化的幅度显著降低,在k>3之后所带来的好处并不是特别明显,
所以我们可以选择k=3作为我们的聚类数目。由于其形状像我们人类的肘部,我们也称其为“肘部法则”。
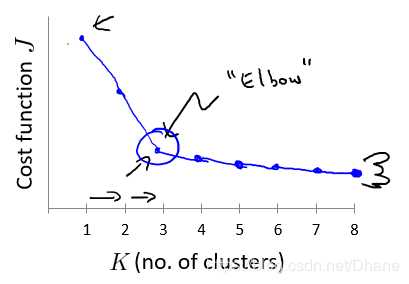
但是实际应用中,k值的变换规律都不是和上图一样存在突变点,多数情况如下图所示:
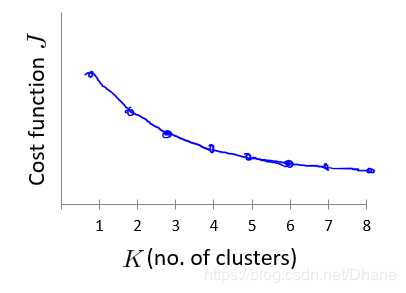
随着k值的增大,其畸变函数也随着不断减小,根本就不存在明显的拐点。
那么这种情况,K值的选择主要还是根据经验以及利用k-means聚类的目的来决定。
聚类中心的初始化
前面提到代价函数的建立,可以方便我们来对k-means算法的结果进行优化,
方便我们察觉出算法迭代过程中的收敛问题,是否达到局部最小化,或者检查算法迭代过程中是否出现问题。
而通过k值的选取也可能使我们的代价函数尽量的减小,以得到更好的聚类效果。那么还有什么其他优化的方法呢?
我们还可以通过选取更优的聚类中心来优化聚类效果。
上面的例图是一个简单的二分类问题,并且不同类之间的界限也比较明显,最后我们得到的聚类结果也相对比较理想。但实际上聚类中心选择的不同,最终的聚类结果肯定也是会不一样的。
比如对于下面这张图:
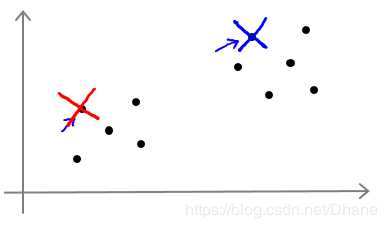
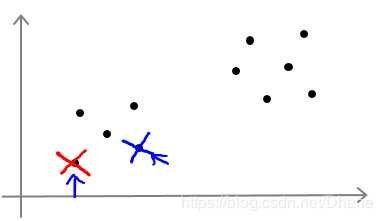
我把初始的聚类中心选择在这两个不同的位置,最后导致的分类结果和迭代次数都会不一样。
聚类中心的选取主要还是以随机为主,并且初始的时候最好是选择数据中的点。
对于多分类,甚至还会出现下面这种情况:
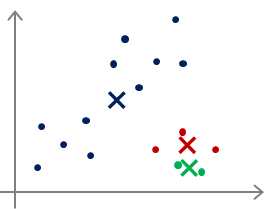
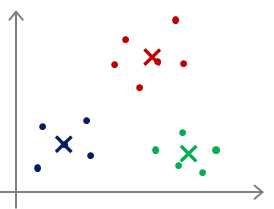
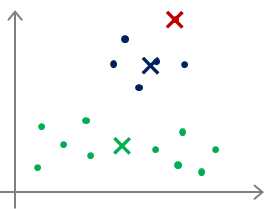
最后很可能仅仅实现了局部最优,把本来不是一类的多个类分为了一类,或者把本来是一类的分成了多个类,
这些都是有可能的。那么对于这种情况怎么办呢?
对于聚类数目K值较小(K<10)的情况下,我们可以多次随机选取不同聚类中心,最后比较各自迭代完成后的畸变函数值,
畸变函数越小,则说明聚类效果更优。但是在k值较大的情况下,比如上百类甚至上千万类,
这时候重新选取不同的聚类中心可能就没有很好的效果了。
以上是关于16、toy数据集上不同聚类算法的比较的主要内容,如果未能解决你的问题,请参考以下文章