数字数据集上的K-均值聚类

Posted 2023-05-06

参考技术A 10、数字数据集上的K-均值聚类

import numpy as np

from time import time

from sklearn import metrics

from sklearn.cluster import KMeans

from sklearn.decomposition import PCA

from sklearn.preprocessing import scale

from sklearn.datasets import load_digits

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

X_digits,y_digits=load_digits(return_X_y=True)

data=scale(X_digits)

n_samples,n_features=data.shape

n_digits=len(np.unique(y_digits))

labels=y_digits

print(labels)

sample_size=300

print(82*'-')

print('init\ttime\tinertia\thome\tcompo\tv_meas\tars\tami\tailhouette')

def bench_k_means(estimator,name,data):

    t0=time()

    estimator.fit(data)

    print('%-9s\t%.2fs\t%i\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f'

        % (name,(time()-t0),estimator.inertia_,

          metrics.homogeneity_score(labels,estimator.labels_),

          metrics.completeness_score(labels,estimator.labels_),

          metrics.v_measure_score(labels,estimator.labels_),

          metrics.adjusted_rand_score(labels,estimator.labels_),

          metrics.adjusted_mutual_info_score(labels,estimator.labels_),

          metrics.silhouette_score(data,estimator.labels_,

                                  metric='euclidean',

                                  sample_size=sample_size)))

bench_k_means(KMeans(init='k-means++',n_clusters=n_digits,n_init=10),name='k-means++',data=data)

bench_k_means(KMeans(init='random',n_clusters=n_digits,n_init=10),name='random',data=data)

#上面初始质心是确定的，把初始质心设定为1进行测试

pca=PCA(n_components=n_digits).fit(data)

bench_k_means(KMeans(n_clusters=n_digits,init='k-means++',n_init=1),name='pca_based',data=data)

print(82*'-')

#在降维的数据上图形化显示

reduced_data=PCA(n_components=2).fit_transform(data)

kmeans=KMeans(init='k-means++',n_clusters=n_digits,n_init=10)

kmeans.fit(reduced_data)

#网格步长

h=0.02

#分配颜色到决策边界。

x_min,x_max=reduced_data[:,0].min()-1,reduced_data[:,0].max()+1

y_min,y_max=reduced_data[:,1].min()-1,reduced_data[:,1].max()+1

xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))

# 获取网格中每个点的标签

Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

# 将结果放入彩色图中

Z = Z.reshape(xx.shape)

plt.figure(1)

plt.clf()

plt.imshow(Z, interpolation='nearest',

          extent=(xx.min(), xx.max(), yy.min(), yy.max()),

          cmap=plt.cm.Paired,

          aspect='auto', origin='lower')

plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)

# 用白色X画出中心体

centroids = kmeans.cluster_centers_

plt.scatter(centroids[:, 0], centroids[:, 1],

            marker='x', s=169, linewidths=3,

            color='w', zorder=10)

plt.title('数字数据集上的K-均值聚类 \n''PCA约简数据\n'

          '白色X标出中心体')

plt.xlim(x_min, x_max)

plt.ylim(y_min, y_max)

plt.xticks(())

plt.yticks(())

plt.show()

k均值聚类

目录

一.k均值简介

二.应用简介

三.算法

四.选择合适的K

五.具体实例

---

 

 

 

一.k均值简介

　　K均值聚类是一种无监督学习，对未标记的数据（即没有定义类别或组的数据）进行分类。 该算法的目标是在数据中找到由变量K标记的组。该算法迭代地工作基于所提供的特征，将每个数据点分配给K个组中的一个。 基于特征相似性对数据点进行聚类。 K均值聚类算法的结果是：

　　1.K簇的质心，可用于标记新数据

　　2.训练数据的标签（每个数据点分配给一个集群）

　　

二.应用简介

　　K均值聚类算法用于查找未在数据中明确标记的组。这可用于判别存在哪些类别特征或用于识别复杂数据集中的未知组。一旦运行算法并定义了组，就可以轻松地将任何新数据分配给正确的组。

　　这是一种多功能算法，可用于任何类型的分组。具体的一些示例是：

　　行为细分：

• 按购买历史记录细分
• 按应用程序，网站或平台上的活动进行细分
• 根据兴趣定义角色
• 根据活动监控创建配置文件

　　库存分类：

• 按销售活动分组库存
• 按制造指标对库存进行分组

　　分类传感器测量：

• 检测运动传感器中的活动类型
• 分组图像
• 单独的音频
• 确定健康监测中的群体

　　检测机器人或异常：

• 从机器人中分离出有效的活动组
• 将有效活动分组以清除异常值检测

　　此外，监视跟踪数据点是否随时间在组之间切换可用于检测数据中的有意义的变化。

三.算法

　　Κ-means聚类算法使用迭代细化来产生最终结果。 算法输入是簇Κ的数量和数据集。 算法从Κ质心的初始估计开始，可以随机生成或从数据集中随机选择。 然后算法在两个步骤之间迭代：

　　1.数据分配步骤：

　　每个质心定义一个簇。 在此步骤中，基于平方欧几里德距离将每个数据点分配到其最近的质心。 更正式地说，如果c_i是集合C中的质心集合，那么每个数据点x都被分配给一个基于集群的集群。

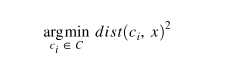
　　其中，dist（·）是标准的欧几里德距离

　　2.质心更新步骤：

　　在此步骤中，重新计算质心。 这是通过获取分配给该质心簇的所有数据点的平均值来完成的。

　　

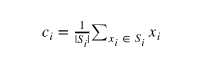
　　该算法在步骤1和步骤2之间迭代，直到满足停止标准（即没有数据点改变，或簇距离的总和最小化，或者达到一些最大迭代次数）。

　　保证该算法收敛于结果。 结果可以是局部最优（不一定是最佳可能结果），这意味着用随机化起始质心评估算法需要次运行可以给出更好的结果。

四.选择合适的K

 

　　该算法找到特定的K个簇和数据集标签。为了找到数据中的簇数，需要针对一系列K值运行K均值聚类算法并比较结果。通常，没有用于确定K的精确值的方法，但是可以使用以下技术获得准确的估计：

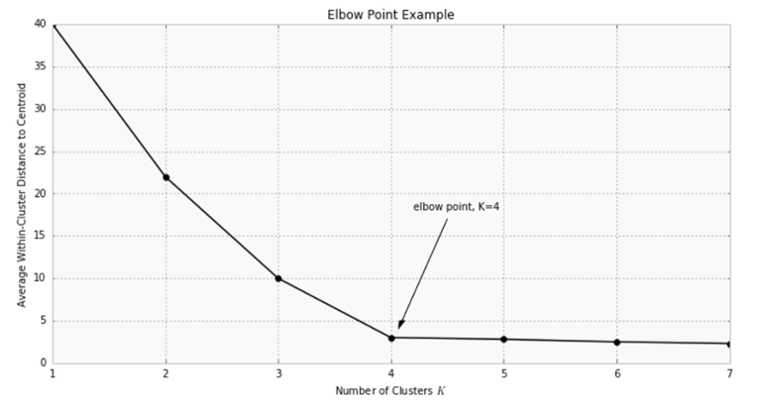
　　通常用于比较不同K值的结果的度量是我方法是数据点与其聚类质心之间的平均距离。由于增加簇的数量将总是减少到数据点的距离，因此当K与数据点的数量相同时，增加K将总是减小该度量，达到零。因此，该指标不能用作唯一目标。相反，绘制作为K的函数的到质心的平均距离，并且可以使用减小率急剧变化的“肘点”来粗略地确定K.

　　存在许多用于验证K的其他技术，包括交叉验证，信息标准，信息理论跳跃方法，轮廓方法和G均值算法。此外，监视跨组的数据点分布可以深入了解算法如何分割每个K的数据。

五.具体实例

　　 下面进行实例聚类。考虑两个驾驶员功能：平均每天行驶距离以及驾驶员超过限速的平均时间百分比> 5英里/小时。 通常，只要数据样本的数量远大于特征的数量，该算法就可以用于任何数量的特征。数据：https://pan.baidu.com/s/1yT3870M8whYlMiQFC9Qq7Q

密码：wtcm

　　1.导入数据并可视化

　　

import numpy as np
import pandas as pd   
import matplotlib.pyplot as plt

df=pd.read_table(‘F:/wd.jupyter/datasets/km_data.txt‘)
X=np.array(df.iloc[:,1:])
plt.scatter(X[:,0],X[:,1])

数据实例：

　

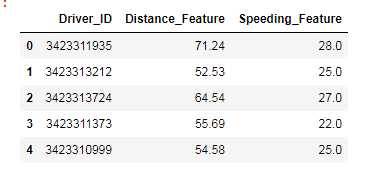
下图显示了4,000个样本，其中x轴为距离特征，y轴为超速特征。

 

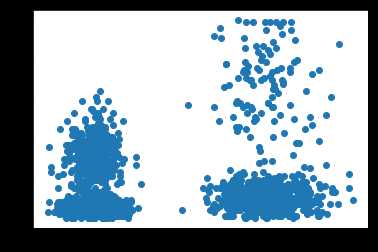
　　2.选择合适的K进行算法迭代

　　首先，选择k=2，利用 scikit-learn进行计算：

 

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=2).fit(X)

 

　　kmeans.labels_. 可以用来查看类别。

　　3.可视化结果

　　利用kmeans.cluster_centers_来查看两个中心点：

　　中心点1：（50.04763438， 8.82875 ）

  中心点2： (180.017075，18.29）
查看聚类结果：

y_pred =kmeans.fit_predict(X)
plt.scatter(X[:,0], X[:,1],c=y_pred)
plt.show()

　　

　　4.重新选择k进行聚类

　　选择k=4重复上述步骤

　　

kmeans2 = KMeans(n_clusters=4).fit(X)
y_pred2 =kmeans2.fit_predict(X)

plt.scatter(X[:,0], X[:,1],c=y_pred2)

plt.show()

　　

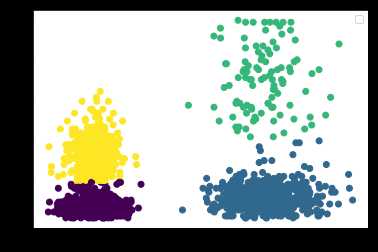
　　当然，存在许多替代聚类算法，包括DBScan，谱聚类和使用高斯混合模型等等。