如何理解皮尔逊相关系数

Posted 2023-02-23

皮尔逊相关系数是比欧几里德距离更加复杂的可以判断人们兴趣的相似度的一种方法。该相关系数是判断两组数据与某一直线拟合程序的一种试题。它在数据不是很规范的时候，会倾向于给出更好的结果。
皮尔逊相关系数理解有两个角度
其一, 按照高中数学水平来理解, 它很简单, 可以看做将两组数据首先做Z分数处理之后, 然后两组数据的乘积和除以样本数。
其二, 按照大学的线性数学水平来理解, 它比较复杂一点,可以看做是两组数据的向量夹角的余弦。
皮尔逊相关的约束条件：
1 两个变量间有线性关系
2 变量是连续变量
3 变量均符合正态分布,且二元分布也符合正态分布
4 两变量独立
在实践统计中,一般只输出两个系数,一个是相关系数,也就是计算出来的相关系数大小,在-1到1之间;另一个是独立样本检验系数,用来检验样本一致性. 参考技术A 皮尔逊相关系数理解有两个角度
其一,按照高中数学水平来理解,它很简单,可以看做将两组数据首先做Z分数处理之后,然后两组数据的乘积和除以样本数
Z分数一般代表正态分布中,数据偏离中心点的距离.等于变量减掉平均数再除以标准差.(就是高考的标准分类似的处理)
标准差则等于变量减掉平均数的平方和,再除以样本数,最后再开方.
所以,根据这个最朴素的理解,我们可以将公式依次精简为:
其二,按照大学的线性数学水平来理解,它比较复杂一点,可以看做是两组数据的向量夹角的余弦.
皮尔逊相关的约束条件
从以上解释,也可以理解皮尔逊相关的约束条件:
1 两个变量间有线性关系
2 变量是连续变量
3 变量均符合正态分布,且二元分布也符合正态分布
4 两变量独立
在实践统计中,一般只输出两个系数,一个是相关系数,也就是计算出来的相关系数大小,在-1到1之间;另一个是独立样本检验系数,用来检验样本一致性.本回答被提问者和网友采纳

Pearson(皮尔逊)相关系数及MATLAB实现

转自：http://blog.csdn.net/wsywl/article/details/5727327

由于使用的统计相关系数比较频繁，所以这里就利用几篇文章简单介绍一下这些系数。

 

相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。

 

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

(1)、当相关系数为0时，X和Y两变量无关系。

(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。

(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

 

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：
相关系数     0.8-1.0     极强相关
                 0.6-0.8     强相关
                 0.4-0.6     中等程度相关
                 0.2-0.4     弱相关
                 0.0-0.2     极弱相关或无相关

 

 

Pearson（皮尔逊）相关系数

 

 

1、简介

 

皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：

公式一：

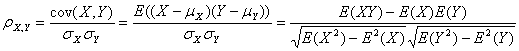
公式二：

公式三：

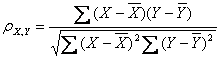
公式四：

以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。

 

 

2、适用范围

 

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

(1)、两个变量之间是线性关系，都是连续数据。

(2)、两个变量的总体是正态分布，或接近正态的单峰分布。

(3)、两个变量的观测值是成对的，每对观测值之间相互独立。

 

 

3、Matlab实现

 

皮尔逊相关系数的Matlab实现（依据公式四实现）：

 

[cpp] view plain copy

 

1. function coeff = myPearson(X , Y)  
2. % 本函数实现了皮尔逊相关系数的计算操作  
3. %  
4. % 输入：  
5. %   X：输入的数值序列  
6. %   Y：输入的数值序列  
7. %  
8. % 输出：  
9. %   coeff：两个输入数值序列X，Y的相关系数  
10. %  
11.   
12.   
13. if length(X) ~= length(Y)  
14.     error(‘两个数值数列的维数不相等‘);  
15.     return;  
16. end  
17.   
18. fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X);  
19. fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 / length(X)));  
20. coeff = fenzi / fenmu;  
21.   
22. end %函数myPearson结束  

 

 

也可以使用Matlab中已有的函数计算皮尔逊相关系数：

 

[cpp] view plain copy

 

1. coeff = corr(X , Y);  

 

 

 

4、参考内容

 

http://zh.wikipedia.org/zh-cn/%E7%9B%B8%E5%85%B3