已知权值集合 如何求其构造的哈夫曼树中带权路径长度之和 只求过程 急急急

Posted 2023-05-06

参考技术A 首先需要构造哈夫曼树，其构造规则是选择两个权值最小的结点，作为左右结点构造成一颗树，这颗树的根权值为左右子树权值大小的和，这个新的权值放入到原有的权值集合中，左右子树权值删除掉
循环上述过程，直到只有一棵树为止。
带权路径长度就是权值结点所在的高度 * 权值大小
带权路径长度之和就是将所有上面的所有求知结果汇总

如何构造哈夫曼树

目录

• 1.什么是哈夫曼树
• 2.哈夫曼树的用处举例
• 3.构造一棵哈夫曼树的思路
• 4.哈夫曼编码实现代码

1.什么是哈夫曼树

设有n个权值{w1,w2,w3,…,wn},构造有n个叶子结点的二叉树,每个叶子结点带权为wi,则其中带权路径长度最小的二叉树称为赫夫曼树或最优二叉树。

哈夫曼树又称最优二叉树。

2.哈夫曼树的用处举例

【举例一】有效减少比较次数

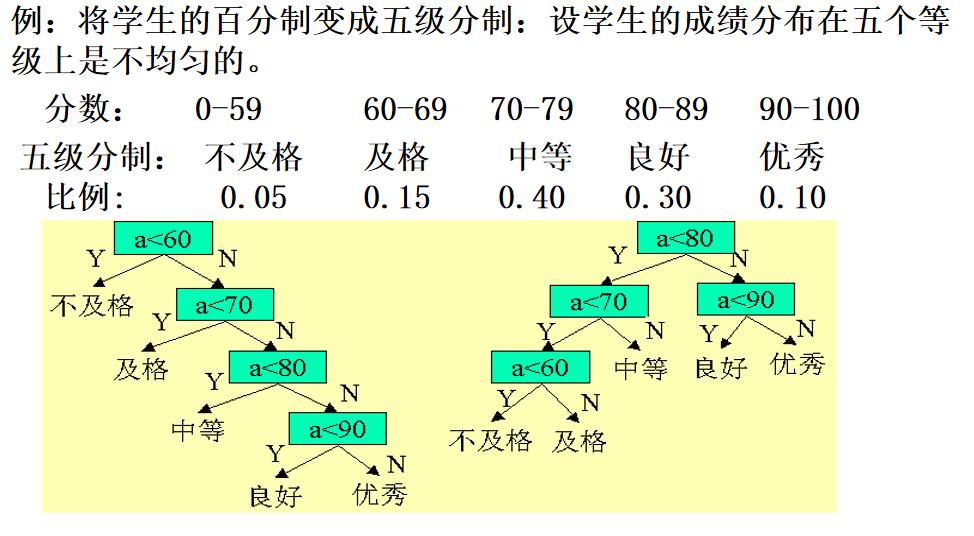
设有 10000 个数据， 左边的数据组织形式需要进行 31500 次比较；而右边的树进行 22000 次比较。

【举例二】有效减少存储空间

哈夫曼编码：保证编码在能够识别的前提下，传递最少的字符。

3.构造一棵哈夫曼树的思路

(1)根据给定的n个权值{w1,w2,w3,…,wn}构成n棵二叉树的集合F={T1,T2,T3,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树均为空.

(2)在集合F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,新二叉树的根结点的权值为其左右子树上根结点的权值之和.

(3)在集合F中删除这两棵树,同时将新得到的二叉树加入F中.

(4)重复步骤(2)、(3),直到F中只含一棵树为止,这棵树就是一棵赫夫曼树.

【举例】给定权值{ 5, 6, 2, 9, 7 }，构造一棵哈夫曼树

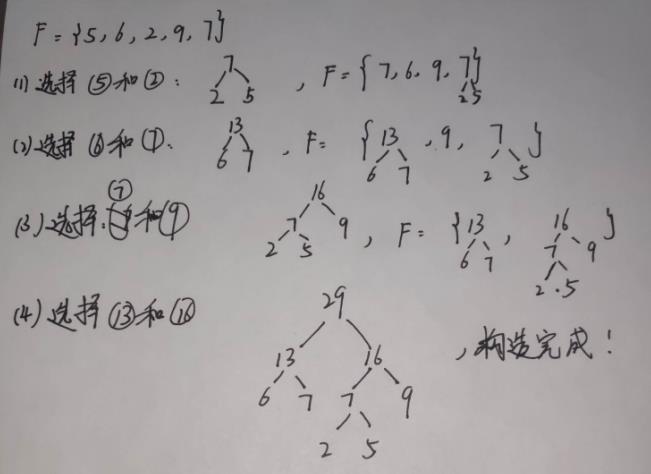
4.哈夫曼编码实现代码

#include <iostream>
#include <stdlib.h>
#include <string.h>
using namespace std;
typedef char NumType;
struct HTNode
{
    float weight;
    int parent;
    int lchild,rchild;
};
typedef HTNode *HuffmanTree;

typedef char ** HuffmanCode;

void Select(HuffmanTree T,int n,int &s1,int &s2)
{
    float min1=99999,min2=99999;
    int i;
    for(i=1;i<=n;i++)
    if(min1>T[i].weight&&T[i].parent==0){min1=T[i].weight;s1=i;}
    for(i=1;i<=n;i++)
    if(min2>T[i].weight&&T[i].parent==0&&T[i].weight!=min1){min2=T[i].weight;s2=i;}
}
void CreateHuffmanTree(HuffmanTree &T,float *w,int n)//w为权值数组首地址，n个叶子结点
{
    int m=2*n-1;//2n-1个结点
    T=(HTNode *)malloc((m+1)*sizeof(HTNode));//多申请一个，从1到m用来存系结点
    HTNode *p;
    int i;
    w++;//w也是从1到n用来存叶子结点的权值
    //初始化存哈夫曼树的数组
    for(i=1,p=T+1;i<=n;i++,w++,p++)*p={*w,0,0,0};
    for(;i<=m;i++,p++)*p={0,0,0,0};
    for(i=n+1;i<=m;i++)
    {
        int s1,s2;//s1,s2分别为集合F中权值最小和次小的下标
        Select(T,i-1,s1,s2);
        T[i].lchild=s1;T[i].rchild=s2;
        T[s1].parent=i;T[s2].parent=i;
        T[i].weight=T[s1].weight+T[s2].weight;
    }
}
void HuffmanCoding(HuffmanTree T,int n)
{
    HuffmanCode HC;
    HC=(char **)malloc((n+1)*sizeof(char *));
    char * cd=(char *)malloc(n*sizeof(char));
    cd[n-1]='\\0';
    int start,c,f;
    int i;
    for(i=1;i<=n;i++)
    {
        start=n-1;
        for(c=i,f=T[c].parent;f!=0;c=f,f=T[f].parent)
        {
            if(T[f].lchild==c){start--;cd[start]='0';}
            if(T[f].rchild==c){start--;cd[start]='1';}
        }
        HC[i]=(char *)malloc((n-start)*sizeof(char));
        strcpy(HC[i],&cd[start]);
    }
    free(cd);
    for(i=1;i<=n;i++)
        cout<<"哈夫曼编码："<<HC[i]<<endl;
}
int main()
{
    int n;
    cin>>n;
    int i;
    char a[100];
    float w[100];
    for(i=1;i<=n;i++)cin>>a[i];
    for(i=1;i<=n;i++)cin>>w[i];
    HuffmanTree HT;
    CreateHuffmanTree(HT,w,n);
    HuffmanCoding(HT,n);
    return 0;
}