一组权值 8,2,5,3,2,17,4 求由此生成的哈夫曼树

Posted 2023-05-07

参考技术A

哈弗曼树就是每回将2个最小的并1个。

过程大约如下：

8,2,5,3,2,17,4

2+2=4

3,4,4,5,8,17

3+4=7

4,5,7,8,17

4+5=9

7,8,9,17

7+8=15

9,15,17

9+15=24

17,24

17+24=41

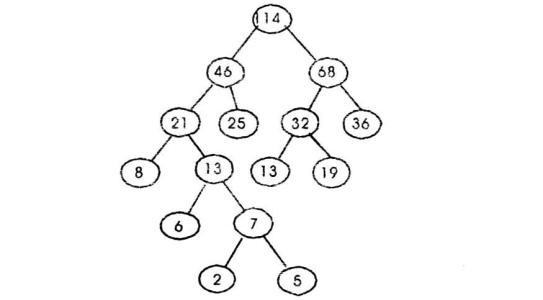
这个树大概是这样的，分号是某个点的两个子节点写完了的意思，意会下：

41

24 17

15 9;

7 8; 4 5;

3 4; 2 2;

哈弗曼树的形态是不一定唯一的

因此这个也是可以的

41

24 17

15 9;

7 8; 4 5;

3 4;

2 2；

她们的带权路径长度分别是

3*4+4*4+8*3+2*4+2*4+5*3+17*1=100

3*4+2*5+2*5+8*3+4*3+5*3+17*1=100

都是带全路径长度最短的生成树

扩展资料：

简介

在计算机数据处理中，哈夫曼编码使用变长编码表对源符号（比如文件中的1个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

哈夫曼编码的起源：

哈夫曼编码是 1952 年由 David A. Huffman 提出的一种无损数据压缩的编码算法。哈夫曼编码先统计出每种字母在字符串里出现的频率，根据频率建立一棵路径带权的二叉树，也就是哈夫曼树，树上每个结点存储字母出现的频率，根结点到结点的路径即是字母的编码，频率高的字母使用较短的编码，频率低的字母使用较长的编码，使得编码后的字符串占用空间最小。

参考资料来源：百度百科-哈夫曼树

福利手游APP下载

新增小号回收账号交易

¥免费分享

手游代理加盟，主推游戏分成70%左右

低投入，分成高

¥198

手游加盟代理自助注册页面

入行手游项目必看教程

¥198

新自由之刃（赤月服）

满攻速魂环版传奇

¥1.76复古

绝世仙王之八荒寻仙录

超高人气仙侠手游

¥无折扣返利

自由之刃2（新）

冰龙魂环复古经典

¥新版复古传奇

查

看

更

多

官方电话官方服务
官方网站福利app代理申请

基于prim算法的网络最小生成树生成得到路径规划

目录

​​一、理论基础​​

​​二、核心程序​​

​​三、测试结果​​

---

一、理论基础

       普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：Vnew = x，其中x为集合V中的任一节点（起始点），Enew = ,为空；

3).重复下列操作，直到Vnew = V：

a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew​​集合​​当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

4).输出：使用集合Vnew和Enew来描述所得到的​​最小生成树​​。

然后将这个整体算法流程图中各个核心步骤的过程进行介绍：

1.根据节点权值进行排序和分类

      根据算法步骤，可以得到最终的各个节点的权值，权值越大，需要充电的节点数量则越大，然后在进行分类的时候，需要综合考虑各个区域的节点的权值，避免某一区域节点权值过大或者过小。这里，选择的是均匀划分方式，即每个MC，对应的节点数量相同，当然也可以其他划分方式，不同的方式得到不同的结果。

2.计算节点权值和节点距离的加权矩阵

采用距离因素和节点权值因素。其中距离矩阵d，其计算方式为：

       然后节点权值则根据前面的几个步骤算法得到W，然后根据距离因素和节点权值因素，得到一个加权的矩阵，即： 

二、核心程序

.................................................

%%
%社团划分
%社团划分
%社团划分
%社团划分
V0_set = (0.9+0.1*rand)*ones(1,CNUM);
K_set  = (0.09+0.01*rand)*ones(1,CNUM);
Eall   = 0;
for cij = 1:CNUM
    
    if cij == 1
       Eall0=0;
    else
       Eall0=Eall;
    end
    
    %初始速度
    V0 = V0_set(cij);% 
    %变速度系数
    K  = K_set(cij);% 
    %总能量
    Ec = 100;
    %随机的剩余能量，每个节点不一样,剩余能量的计算，需要根据多个车辆进行计算
    ei = 10+10*rand(1,N);
    %算法一所得的社团表
    Cj1;
    %各个社团表的中心点
    Xc1;
    Yc1;
    %能量级数ε的近似能量
    pa = 8*rand(1,N);
    Cj = Cj1;

    Tl = 200;
    Ei = ei/CNUM;

    ind   = 0;
    %不同车的位置
    Xmc   = [];
    Ymc   = [];
    theta = 45/180*pi;


    %初始最优路径  
    Nl= length(Xc1);
    a = 0.6;
    t0= 10;
    tf= 0.001;
    xx= Xc1;
    yy= Yc1;

    figure(2);
    for j = 1:length(C)
        tmp = Cj,1;
        X0  = Xo(tmp);
        Y0  = Yo(tmp);
        plot(X0,Y0,colorsj);
        hold on
        Xc(j)= mean(X0);
        Yc(j)= mean(Y0);
        for i = 1:length(tmp)
            dist(i) = sqrt((Xc(j)-X0(i))^2 + (Yc(j)-Y0(i))^2);
        end
        plot2(Xc(j),Yc(j),max(dist)); 
        hold on
    end
    plot(Xc,Yc,rs,LineWidth,2,MarkerEdgeColor,b,MarkerFaceColor,y,MarkerSize,10)
    hold on

    xx1 = [xx,xx(1)];
    yy1 = [yy,yy(1)];
    for i=1:Nl
        for j=1:Nl
            if i==j
               continue;
            end
            d(i,j)=sqrt((xx(i)-xx(j)).^2+(yy(i)-yy(j)).^2);
        end
    end
    gen=1;
    while gen<=5
          gen
          [f,T]=func_trp(a,d,t0,tf);
          opfs(gen)    = f;
          paths(gen,:) = T;
          gen          = gen+1;
    end 
    for i=1:Nl
        xx2(i)=xx(T(i));
        yy2(i)=yy(T(i));
    end
    xx2(Nl+1)=xx(1);
    yy2(Nl+1)=yy(1);
    hold on
    plot(xx2,yy2);
    title(社团划分前的初始路径规划);


    %线路进行插值获得不同时刻MC的位置
    dall = 0;
    %模拟变速度
    for i = 1:length(xx2)-1;
        Va       = V0 + K*randn;
        dall     = sqrt((xx2(i)-xx2(i+1))^2 + (yy2(i)-yy2(i+1))^2); 
        SCALE(i) = dall/Va;
    end
    %插值，用来模拟路径点坐标
    Xlp0=[];
    Ylp0=[];
    for i = 1:length(xx2)-1;
        Xlp0=[Xlp0,[xx2(i):(xx2(i+1)-xx2(i))/SCALE(i):xx2(i+1)]];
        Ylp0=[Ylp0,[yy2(i):(yy2(i+1)-yy2(i))/SCALE(i):yy2(i+1)]];
    end

    tk    = 0.1;
    Tt    = tk:tk:length(Xlp0)*tk;

    Esave = zeros(length(Tt),N);
    Cj2   = zeros(length(Tt),length(C));

    %根据路径进行mc移动，然后进行社团划分
    %根据路径进行mc移动，然后进行社团划分
    for t = Tt
        ind = ind+1;
        rng(ind);
        %mc移动
        Xmc(ind) = Xlp0(ind);
        Ymc(ind) = Ylp0(ind);
        %根据mc位置，对路过的社团进行充电
        ischarge = zeros(1,length(Cj));
        for j=1:length(Cj)%依次计算每个社团
            tmp = Cj,1;
            X0s = Xo(tmp);%社团中各个点的坐标
            Y0s = Yo(tmp);
            %计算社团的中心点，覆盖范围
            Xc  = mean(X0s);
            Yc  = mean(Y0s);
            for j2 = 1:length(tmp)
                dr(j2) = sqrt((Xc - X0s(j2))^2 + (Yc - Y0s(j2))^2); 
            end
            Rr  = max(dr);
            Rl  = sqrt((Xc - Xmc(ind))^2 + (Yc - Ymc(ind))^2); 
            if Rl <= Rr%进入某个社团
               ischarge(j) = 1;
            else
               ischarge(j) = 0; 
            end
        end

        for j=1:length(ischarge)
            if ischarge(j) == 1%进行充电
               tmp = Cj,1;
               X0s = Xo(tmp);%社团中各个点的坐标
               Y0s = Yo(tmp);
               Xc  = mean(X0s);
               Yc  = mean(Y0s);
               for j2 = 1:length(tmp)
                   if t == 1
                      Ei(tmp(j2)) = ei(tmp(j2))/CNUM; 
                   else
                      %计算距离
                      dst = sqrt((X0s(j2)-Xc)^2 + (Y0s(j2)-Yc)^2);
                      lvel= floor(dst/100)+1; 

                      Ei(tmp(j2)) = Ei(tmp(j2)) + pa(tmp(j2))*(1+0.5)^(-lvel)*tk;  
                      if Ei(tmp(j2)) >= Ec/CNUM
                         Ei(tmp(j2)) = Ec/CNUM; 
                      end
                      %容量限制
                      if Ei(tmp(j2)) >= Ecap
                         Ei(tmp(j2)) = Ecap; 
                      end                      
                   end
               end
            else%不充电
               for j2 = 1:length(tmp)
                   Ei(tmp(j2)) = Ei(tmp(j2)); 
               end
            end
        end

        %PN分类
        Xpc=[];
        Ypc=[];
        for j=1:length(C)
            tmp  = Cj,1;
            X0s = Xo(tmp);%社团中各个点的坐标
            Y0s = Yo(tmp);
            %计算社团总能量
            Eall = Eall0 + sum(Ei(tmp));

            if Eall/(Ec*length(tmp)) >= 0.9
               Cj2(ind,j) = 1;%P
               %P型社团的中心
               Xpc=[Xpc,mean(X0s)];
               Ypc=[Ypc,mean(Y0s)];
            else
               Cj2(ind,j) = 0;%N
            end
        end
        Esave(ind,:) = Ei;
        %将P型社团的中心视为其停留点参与算法四的路线制定
        Xpind  = [Xpc];
        Ypind  = [Ypc];
    end

    %获得最终划分结果
    Cpn0 = sum(Cj2);
    Cpn  = zeros(size(Cpn0));
    inx  = find(Cpn0>0);
    Cpn(inx) = 1;
    Cpn


    %显示划分结果
    figure(3);
    for j = 1:length(Cj)
        tmp = Cjj,1;
        X0  = Xo(tmp);
        Y0  = Yo(tmp);
        plot(X0,Y0,colorsj);
        hold on
        Xc(j)= mean(X0);
        Yc(j)= mean(Y0);
        for i = 1:length(tmp)
            dist(i) = sqrt((Xc(j)-X0(i))^2 + (Yc(j)-Y0(i))^2);
        end
        if Cpn(j) == 1
           plot3(Xc(j),Yc(j),max(dist)); 
        else
           plot4(Xc(j),Yc(j),max(dist)); 
        end
        hold on
    end
    plot(Xc,Yc,rs,LineWidth,2,MarkerEdgeColor,b,MarkerFaceColor,y,MarkerSize,10)
    title(社团划分结果（Red：P；Black：N），Yellow：P&N中心点);
    
    
    Xmc_setcij   = Xmc;
    Ymc_setcij   = Ymc;
    Esave_setcij = Esave;  
end
Cpn_set = Cpn; 
..............................................

三、测试结果

A26-08