无监督学习DBSCAN聚类算法原理介绍，以及代码实现

Posted 2021-04-08 Python爱好者社区

博客：http://blog.csdn.net/zzz_cming

作者好文推荐：

前言：无监督学习想快一点复习完，就转入有监督学习

聚类算法主要包括哪些算法？

主要包括：K-means、DBSCAN、Density Peaks聚类（局部密度聚类）、层次聚类、谱聚类。

若按照聚类的方式可划分成三类：第一类是类似于K-means、DBSCAN、Density Peaks聚类（局部密度聚类）的依据密度的聚类方式；
第二种是类似于层次聚类的依据树状结构的聚类方式；
第三种是类似于谱聚类的依据图谱结构的聚类方式。

什么是无监督学习？

• 无监督学习也是相对于有监督学习来说的，因为现实中遇到的大部分数据都是未标记的样本，要想通过有监督的学习就需要事先人为标注好样本标签，这个成本消耗、过程用时都很巨大，所以无监督学习就是使用无标签的样本找寻数据规律的一种方法

• 聚类算法就归属于机器学习领域下的无监督学习方法。

无监督学习的目的是什么呢？

• 可以从庞大的样本集合中选出一些具有代表性的样本子集加以标注，再用于有监督学习

• 可以从无类别信息情况下，寻找表达样本集具有的特征

分类和聚类的区别是什么呢？

• 对于分类来说，在给定一个数据集，我们是事先已知这个数据集是有多少个种类的。比如一个班级要进行性别分类，我们就下意识清楚分为“男生”、“女生”两个类；该班又转入一个同学A，“男ta”就被分入“男生”类；

• 而对于聚类来说，给定一个数据集，我们初始并不知道这个数据集包含多少类，我们需要做的就是将该数据集依照某个“指标”，将相似指标的数据归纳在一起，形成不同的类；

• 分类是一个后续的过程，已知标签数据，再将测试样本分入同标签数据集中；聚类是不知道标签，将“相似指标”的数据强行“撸”在一起，形成各个类。

一、DBSCAN聚类

定义：DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，DBSCAN算法将“簇”定义为密度相连的点的最大集合。

1、传统的密度定义：基于中心的方法

传统的密度定义方法——事先给定半径r，数据集中点a的密度，要通过落入以点a为中心以r为半径的圆内点的计数（包括点a本身）来估计。很显然，密度是依赖于半径的。如下图所示： 

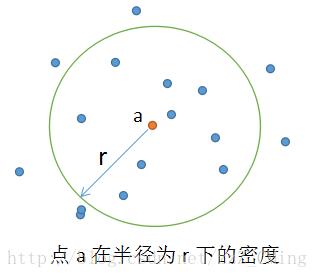
2、DBSCAN中依照密度，对样本点的划分

基于以上密度的定义，我们可以将样本集中的点划分为以下三类：

• 核心点：在半径r区域内，含有超过MinPts数目（最小数目）的点，称为核心点；

• 边界点：在半径r区域内，点的数量小于MinPts数目，但是是核心点的直接邻居；

• 噪声点：既不是核心点也不是边界点的点

下图可以很清楚的区分三种点： 

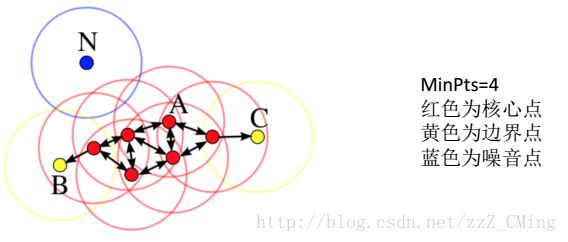
依照上图以及三种点的定义，可以得到：噪声点是不会被聚类纳入的点，边界点与核心点组成聚类的“簇”。

3、介绍三个有趣的概念

• 直接密度可达：在给定一个对象集合D，如果p在q的r领域内，且q是一个核心点对象，则称对象p从对象q出发时是直接密度可达的

• 密度可达：在给定对象集合D中，如果存在一个对象链q–>e–>a–>k–>l–>p，任意相邻两个对象间都是直接密度可达的，则称对象p是对象q关于r邻域内、MinPts数目下，是密度可达的；

• 密度相连：如果在对象集合D中存在一个对象O，使得对象p和q都是从O关于r邻域内、MinPts数目下，是密度相连的。

如下图所示：r用一个相应的半径表示，设MinPts=3，分析Q、M、P、S、O、R这5个样本点之间的关系。 

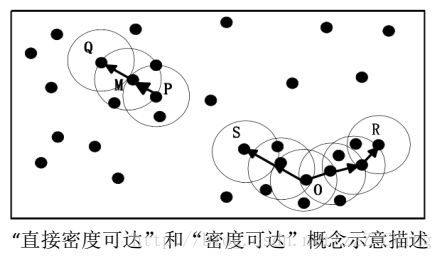
根据以上概念可知：由于有标记的各点M、P、O和R的r邻域均包含3个以上的点，因此它们都是核对象；M是从P的“直接密度可达”；Q是从M的“直接密度可达”；基于上述结果，Q是从P的“密度可达”；但P从Q是无法“密度可达”（非对称的）；类似的，S和R都是从O的“密度可达”；O、R都是从S的“密度相连”。

也就是说：核心点能够连通（密度可达），它们构成的以r为半径的圆形邻域相互连接或重叠，这些连通的核心点及其所处的邻域内的全部点构成一个簇。

4、DBSCAN聚类算法原理

1. DBSCAN通过检查数据集中每个点的r邻域来搜索簇，如果点p的r邻域包含多于MinPts个点，则创建一个以p为核心对象的簇；

2. 然后， DBSCAN迭代的聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并；

3. 当没有新的带你添加到任何簇时，迭代过程结束。

DBSCAN聚类算法效果展示如下图： 

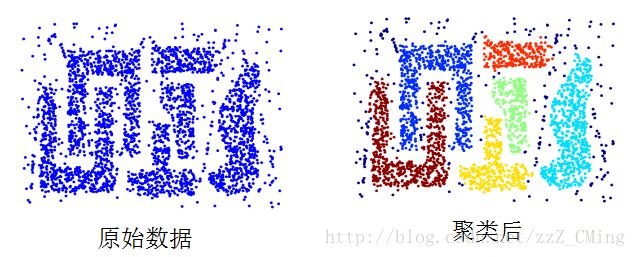
5、DBSCAN聚类算法优缺点

优点：基于密度定义，可以对抗噪声，能处理任意形状和大小的簇

缺点：当簇的密度变化太大时候，聚类得到的结果会不理想；对于高维问题，密度定义也是一个比较麻烦的问题。

6、DBSCAN聚类算法

# -*- coding:utf-8 -*- # -*- author：zzZ_CMing # -*- 2018/04/10；15:38 # -*- python3.5 import numpy as np import matplotlib.pyplot as plt from sklearn import datasets import matplotlib.colors # 创建Figure fig = plt.figure() # 用来正常显示中文标签 matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # 用来正常显示负号 matplotlib.rcParams['axes.unicode_minus'] = False X1, y1 = datasets.make_circles(n_samples=5000, factor=.6,                                      noise=.05) X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2,                             centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9) # 原始点的分布 ax1 = fig.add_subplot(311) X = np.concatenate((X1, X2)) plt.scatter(X[:, 0], X[:, 1], marker='o') plt.title(u'原始数据分布') plt.sca(ax1) """ # K-means聚类 from sklearn.cluster import KMeans ax2 = fig.add_subplot(312) y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.title(u'K-means聚类') plt.sca(ax2) """ # DBSCAN聚类 from sklearn.cluster import DBSCAN ax3 = fig.add_subplot(313) y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.title(u'DBSCAN聚类') plt.sca(ax3) plt.show()

效果展示：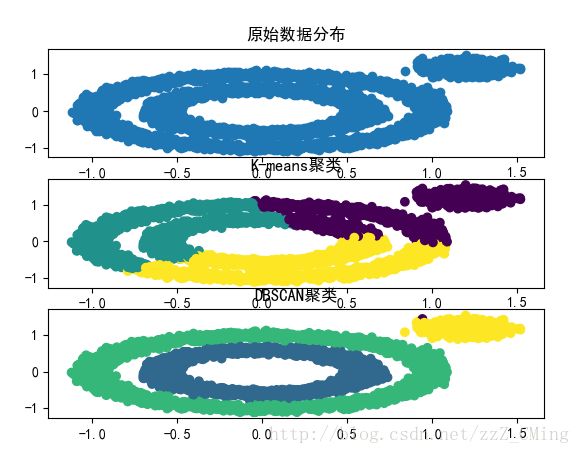

赞赏作者

Python爱好者社区历史文章大合集：

小编的Python入门视频课程！！！

崔老师爬虫实战案例免费学习视频。

丘老师数据科学入门指导免费学习视频。

陈老师数据分析报告制作免费学习视频。

玩转大数据分析！Spark2.X+Python 精华实战课程免费学习视频。

丘老师Python网络爬虫实战免费学习视频。