物以类聚，人以群分，一文读懂聚类算法

Posted 2021-04-08 数学观察世界

所谓人以类聚，物以群分。人都喜欢跟自己像的人聚在一起，这些人或者样子长得比较像，或者身高比较像，或者性格比较像，或者有共同的爱好，也就是身上有某些特征是相似的。

而跟自己像的人聚在一起的过程，其实就是寻找朋友的过程，比如A认识B，因为跟B兴趣相近于是成为了朋友，通过B又认识了C，发现兴趣较一致于是也成为了朋友，那么ABC三个人就是一个朋友群，这个朋友群的形成，是自下而上的迭代的过程。在100个人当中，可能有5个朋友群，这5个朋友群的形成可能要2个月。

而聚类算法，跟以上的过程很像。

聚类算法，是把距离作为特征，通过自下而上的迭代方式（距离对比），快速地把一群样本分成几个类别的过程。

有人可能会说，干嘛要聚类啊，肉眼看猪是猪牛是牛这不一下就分开了么，那如果是一万头猪跟牛，你能一下分开么？

又有人说猪跟牛长的那么不一样，一下就看出来了，还用机器？其实猪跟牛看的出分别是因为他们的外形太不一样。实际上样本可能有几个甚至几十个维度，光对比其中1,2个维度基本分不出差别。

所以聚类算法，一般是面向大量的，同时维度在2个或2个以上的样本群。

前面讲到，聚类算法是根据样本之间的距离来将他们归为一类的，这个距离不是普通的距离，理论上叫做欧氏距离。

为什么不用普通的距离就好，用这么拗口的欧式距离？那是为了衡量高于三维空间的样本之间的距离。在二维和三维空间里，欧式距离就是我们理解的普通的距离。

在多维空间里，假设两个样本为a(x1,x2,x3,x4...xn)，b(y1,y2,y3,y4...yn)。那么他们之间的欧式距离的计算公式是

那么聚类算法，是怎么通过迭代的方式，将样本聚成几个类别的呢？

有一种最经典的K-Means聚类方法，他是这样运作的：

1、在样本中随机选择K个点，作为每个类别的初始中心点，这K是自己定的，假如你想将样本分成3个类K就等于3,4个类K就等于4；

2、计算所有样本离这K个初始中心点的距离并分别进行比较，选出其中最近的距离并把这个样本归到这个初始中心点的类别里，即总共划分成K个类别；

3、舍弃原来的初始中心点，在划分好的K个类别里分别计算出新的中心点，使得这些中心点距离他类别里的所有样本的距离之和最小；

4、判断新获得的中心点是否与旧中心点一样，如不一样则回到第2步，重新计算所有样本离这K个新的中心点的距离并进行比较，选出其中最近的距离并归到这个新的中心点的类别里，继续下面的步奏；如一样则完成，即收敛。

可以用下面的图很好地说明

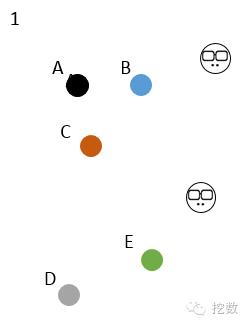
有ABCDE5个样本，一开始选定右边的2个初始中心点，K=2，大家颜色都不一样，谁都不服谁；

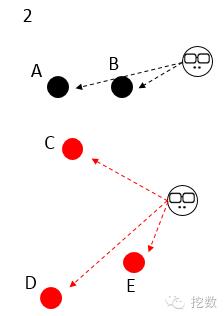
5个样本分别对比跟2个初始中心点的距离，选距离近的傍依，这时5个样本分成红黑2群；

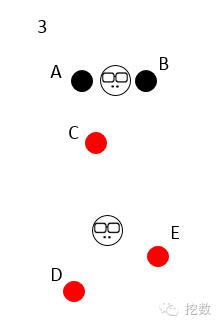
然后开始换老大啦，2个初始中心点消失，重新在2个类分别中心的位置出现2个新的中心点，这2个新的中心点离类别里样本的距离之和必须是最小的；

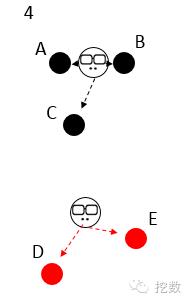
新的老大出现，类别的划分也不一样啦，C开始叛变，皈依新老大，因为他离新老大更近一点；

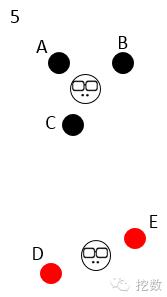
新的老大消失，新新老大出现，发现划分的类别没有变化，帮派稳定，于是收敛。

用Python写了一个简单的聚类算法：

import matplotlib.pyplot as plt import random import math from copy import copy #寻找新的中心点的函数 def new(group):    minimum=10000    o=[]    for x1 in range(min(group['x']),max(group['x'])):        for y1 in range(min(group['y']),max(group['y'])):            j=0            red_sum=0            while j<=len(group['x'])-1:                red_sum+=math.sqrt((group['x'][j]-x1)**2+(group['y'][j]-y1)**2)                j+=1            o.append(red_sum)            if(red_sum<minimum):                minimum=copy(red_sum)                x2=copy(x1)                y2=copy(y1)    return x2,y2 #根据中心点聚类并且着色的函数 def color(a,b,x,y):    i=0    red={'x':[],'y':[]}    blue={'x':[],'y':[]}    black={'x':[],'y':[]}    while i<=90:        distance0=math.sqrt((int(a[i])-x[0])**2+(int(b[i])-y[0])**2)        distance1=math.sqrt((int(a[i])-x[1])**2+(int(b[i])-y[1])**2)        distance2=math.sqrt((int(a[i])-x[2])**2+(int(b[i])-y[2])**2)        if (min(distance0,distance1,distance2)==distance0):            plt.plot(a[i],b[i],'ro',color='red')            red['x'].append(int(a[i]))            red['y'].append(int(b[i]))        elif (min(distance0,distance1,distance2)==distance1):            plt.plot(a[i],b[i],'ro',color='blue')            blue['x'].append(int(a[i]))            blue['y'].append(int(b[i]))        else:            plt.plot(a[i],b[i],'ro',color='black')            black['x'].append(int(a[i]))            black['y'].append(int(b[i]))        i+=1    return red,blue,black def main():    #读取数据    file=open('d:/kmeans/data.txt')    a=[]    b=[]    for line in file.readlines():        data=line.strip().split(',')        a.append(data[0])        b.append(data[1])    #随机选取3个初始中心点    x=[random.randint(1,20),random.randint(1,20),random.randint(1,20)]    y=[random.randint(1,20),random.randint(1,20),random.randint(1,20)]    red,blue,black=color(a,b,x,y)    plt.plot(x[0],y[0],'x',color='red',markersize=15)    plt.plot(x[1],y[1],'x',color='blue',markersize=15)    plt.plot(x[2],y[2],'x',color='black',markersize=15)    plt.axis([0,25,0,25])    plt.show()    #循环执行函数，直到收敛    while (x[0],y[0]!=new(red)) or (x[1],y[1]!=new(blue)) or (x[2],y[2]!=new(black)):        x[0],y[0]=new(red)        x[1],y[1]=new(blue)        x[2],y[2]=new(black)        red,blue,black=color(a,b,x,y)        plt.plot(x[0],y[0],'x',color='red',markersize=15)        plt.plot(x[1],y[1],'x',color='blue',markersize=15)        plt.plot(x[2],y[2],'x',color='black',markersize=15)        plt.axis([0,25,0,25])        plt.show()    file.close()       if __name__=='__main__':    main()

第一次聚类时，分布是这样的

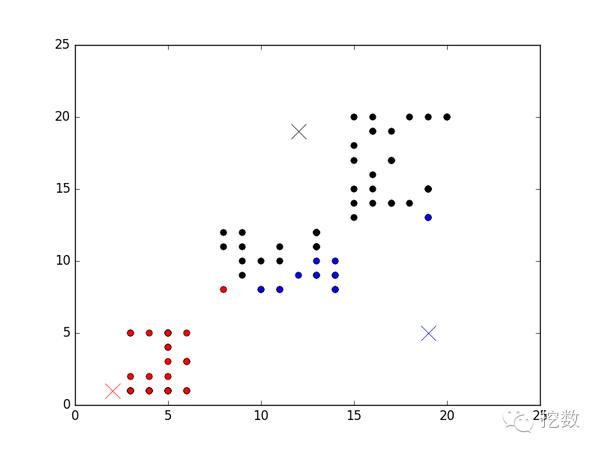
第二次聚类时，分布是这样的

收敛时，分布是这样的

文章转载自挖数

版权归作者所有